2. 5 Сурет. Бас сүйек жазықтығының сагиттальды иінтірегі [5]
Иінтіректің тепе- теңдік шарты: F* а=R* b.
Иінтіректің екінші деңгейі адамға аяқтың ұшымен тұруға, және жүру барысында тіреуші аяқтың ауырлық күшін қозғалысқа бағыттауына әсер етеді.
2. 6 Сурет. Табан мен оған әсер ететін күштер бейнеленген.
2. 6 Сурет. Аяқтың ұшымен тұру [5]
Айналу білігі (O) табан сүйегінің басы арқылы өтеді; табанға бір жақта орналасқан екі күш әсер етеді:
Ауырлық күші (R) бүкіл денеге әсер ететін күштің жартысына тең; бұл күштің көлемі b әрпімен белгіленеді, ол табан сүйектерінің ара- қашықтығын өлшейді.(әдетте 12 см)
Бұлшық еттің тартылыс күші (F), өкше сүйегі мен сіңірге беріледі, бұл күштің көлемі a әрпімен белгіленеді, ол тірек пен сіңірдің ара- қашықтығы.(әдетте 18 см)
Иінтіректің тепе- теңдік шарты: F* а=R* b. Бұл жағдайда а>b, яғни F<R. Иінтірек күште жеңгенімен, қозғалыста ұтылысқа ұшырайды.
Иінтіректің екінші деңгейі адамның білегінде жұмыс істейді.
2. 7 Сурет. Білек пен оған әсер ететін күштер бейнеленген.
2. 7 Сурет. Білек сүйектері, тіректі ұстап тұруы
Айналу білігі (O) шынтақ буынында орналасқан; иінтірекке бір ось бойында екі күш әсер етеді:
Ауырлық күші (R)жүк салмағына тең; бұл күштің көлемі b әрпімен белгіленеді;
Бұлшық еттің тартылыс күші (F), бұлшық ет күшінің көмегімен беріледі; бұл күштің көлемі а әрпімен белгіленеді.
Иінтіректің тепе- теңдік шарты: F* а=R* b. Бұл жағдайда а>b, яғни F<R. Иінтірек күштен 8 есеге ұтылады. Бұл құрылғы пайдалануға ыңғайлы ма? Былай қарағанда ыңғайсыз, себебі күштің шығындалуы болады. Бірақ механиканың «алтын ережесіне» сәйкес күштің шығындалуы қозғалыстың жылдамдауына әсер етеді: тіректің қозғалысы бұлшық ет шамаларының қозғалысынан 8 есе көп болады. Бір уақытта, қозғалыстың жылдамдығы артады: тірек бұлшық еттен 8 есе көп қозғалады.
Сондықтан, адам денесіне бұлшық еттерді бекіту аяқтардың жылдам қозғалысына байланысты. Адамның қолдары осы принцип бойынша әрекет етпегенде, ол баяу қызмет етер еді [5].
2.2. Жердің ауырлық даласында екі аяқпен жүру кезінде дене массасының қозғалыс орталығы
Адам денесінің орталық массасы екі аяқпен жүру кезінде парабола бойымен қозғалады(2.8 сурет). Мұндай қозғалыс кезінде аяқтың қозғалысы есебінен орталық масса көтеріледі, жүйе жоғары потенциалдық энергия әсерінен үздіксіз күйге өтеді. Содан кейін массаның орталық қозғалысы ауырлық күшінің әсерінен қозғалысқа түседі. Гамильтон мен Лагранжтың минимумдар туралы көзқарасына байланысты, Жердің ауырлық даласында нүктелі массаның парабола бойымен қозғалуы тиімді шешім болып табылады[9].
2.8 Сурет. Масса орталығының бір қадамға өзгергендегі жүрген жолы
Массаның орталығы О нүктесінде mv0импульсін алады,ал В нүктесіде салмақтың бір аяқтан екінші аяққа ауысуы және осы үдерісті қайталайды.
Гамильтон- Остроград принципі бойынша қозғалыс функциясы келесідей:
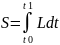(2.1)
Дене массасы орталығының қозғалысының жүрген жолын қарастырайық: парабола және түзу (кесінді OA Ox осі бойында).
Параболалық қозғалысты келесі өрнекпен анықтайды:
,
;
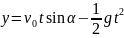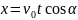(2.2)
Уақыт кезеңінде
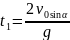(2.3)
Тіреуші аяқ ауысады.
Масса орталығы бір циклда ОА қашықтығына қозғалады:
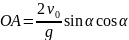(2.4)
(2.2)- (2.4) формуласында t- уақыт, g- еркін құлау жылдамдығы.
Гамильтон- Остроград принципі бойынша оның қозғалысы бір уақытта бірдей жолмен іске асады, сондықтан жылдамдық v ОА кесіндісінің қозғалысына тең:
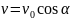(2.5)
Потенциалдық П мен кинетикалық Т энергияларының жүрген жолдары:
(2.6)
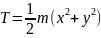(2.7)-
параболалық қозғалыс үшін;
(2.8)-
түзусызықты қозғалыс үшін.
Лагранж функциясы
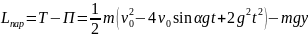(2.9a)
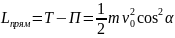(2.9б)
Гамильтонның параболалық қозғалысқа әсері
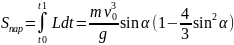(2.9в)
Гамильтонның түзусызықты қозғалысқа әсері
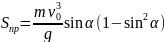(2.9г)
Мопертюи – Лагранж принципін қарастырайық. Лагранжтың әрекеті W кертартпа системаларда қолданылады делінген[9].
(2.9д)
Сонымен қатар, Мопертюи- Лагранж принципінде , толық энергия Н = Т+ П қозғалуы және қозғалу жолдары бірдей, уақыттары әртүрлі болып келеді.
Н
= Т+ П болғандықтан, бастанқы жылдамдық
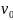параболалық және түзусызықты қозғалыста
бірдей, уақыттары әртүрлі.
Парабола үшін уақыт (2.3) формуласымен өрнектеледі, ал түзусызықты қозғалыс үшін келесі формула қолданылады:
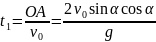(2.10)
Кинетикалық энергия параболалық қозғалыс үшін
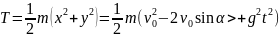(2.11)
Кинетикалық энергия түзусызықты қозғалыс үшін
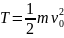(2.12)
Параболалық жолға Лагранж әрекеті
(2.13)
Түзусызықты жолға
(
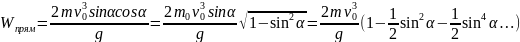2.14 )
(2.13), ( 2.14 ) формулаларын қорыта келе мына өрнекті аламыз:
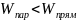(2.15)
Сондықтан, Лагранж бойынша әрекет ету параболалық жолға қарағанда түзусызықты жолда көп қолданылады екен.
Орын ауысиыру кезінде мейлінше шығынды азайту үшін көптеген биологиялық нысандар Жердің гравитациясын қолданған. Мысалы, құстар мен жұлдызқұрттар мейлінше жоғары көтерілуі үшін қолданады.