1.7 Онзагер принципі

Қайтымсыз процессті тұтас орта үлгілерінде (1.59) теңдеуін жинақтап үшін келесі теңдеуді қабылдайды

(1.61)

мұндағы « термодинамикалық күштер» ; - «ағыстар» қайтымсыздық туралы термодинамиканың екінші заңы талап ету күшіне термодинамикалық күштер және ағыстар тәуелсіз болуы мүмкін емес.

Олардың арасындағы тәуелділік көп жағдайда сызықтық қатынас пен суреттеледі

= (1.62)

(1.62) теңдеу кинетикалық қатынас – кинетикалық коэффициенті.Кинетикалық қатынастың мысалы Фурьенің жылуөткізгіштің заңы (1.45), (1.46) болып табылады.

Онзагер принципі- кинетикалық коэффициент симметриялық принципі егер аргумент ортасында аксиалды вектор болмаса , онда

екеніндәлелдейді.

Егер дисппативті процесстер (үрдістер) аксиалды векторларға тәуелді болса, мысалы магнит өрісінің кернеулігінен , онда алдыңғы теңдіктер = арақатынасымен алмастырылады.

1.8. Еркін (бос) энергия, энтальпия, Гиббстің термодинамикалық потенциалы

Тұтас ортаның термодинамикалық қасиетін сипаттауда, ішкі энергиядан u, температураданT, энергия тығыздығынан sбасқа, өзге де функция жағдайлары қолданылады, көп жағдайда еркін энергия сұйықтар мен газдар үшін энтальпия (жылусыйымдылық) қатты деформациялық орта үшін Гиббстің термодинамикалық потенциалы (барлық функциялар масса бірлігіне қатысты) қолданылады.

1.9. Тұтас ортаның кейбір математикалық моделі (үлгісі)

Механикада тұтас ортаның нақты процесінің (үдерісінің) есептеулерінде термодинамика заңдары қолданылады. Орта қозғалысын сипаттайтын, ал екінші заң мүмкін болатын процестер тобын (класын) анықтайтын энергияның теңдеуі толық теңдеулер жүйесіне кіреді.

Сонымен қатар термодинамика заңдары тұтас ортаның жаңа үлгілерін (модельдерін) алу үшін қолданылады. Тұтас ортаның математикалық үлгісін(моделін) беру - ортаның тепе-теңдігін немесе қозғалысын сипаттауға мүмкіндік беретін толық (тұйық) теңдеулер жүйесін беру дегенді білдіреді.

Кез келген ортаның үлгісі (моделі) үшін теңдеулердің толық жүйесі мыналардан тұрады:

• массаның сақталу заңын сипаттайтын, қозғалыс санын, қозғалыс пен энергия сандардарының моменттерін, сонымен қоса термодинамиканаң екінші заңын анықтайтын, барлық орта үшін орындалуы қажет әмбебап теңдеулерден;

• анықтауыштар деп аталатын нақты ортаның берілетін қасиеттерінің өзара қатынасынан.

Анықталатын арақатынастар арасында күй параметрлерінің тепе-теңдігі аралығында байланыс болуы мүмкін. Онда оларды күй теңдеулері деп атайды, мысалы p=RρT арасындағы байланыс жетілдірілген газ үшін. Сонымен қатар үдерісті (процесті) сипаттайтын параметрлер арасындағы байланыс. Оларды көп жағдайда кинетикалық байланыс деп атайды, мысалы тұтқыр сұйықтықта кернеулер мен деформация жылдамдықтары арасындағы байланыс. Анықталатын арақатынастарды жаза отырып, орта тәртібі жайлы тәжірибелі деректерін және теңдеудің түрлері туралы жорамалдарын ұсынады. Бұл гипотезалар (болжамдар, жорамалдар) термодинамика заңдарымен келісімді болуы қажет. Параметрлер арасындағңы байланысты қолдану жалпы заңдардан алынған үлгіні (модельді) құруға қажетті жорамалдар мен тәжірибелер санын қысқартады.

Тұтас ортаның кейбір классикалық үлгісін анықтайтын арақатынасты келтірейік. Бұл арақатынастар орта моделін құру үшін минимальды жүйелерді ұсынбайды.

Тұтас ортаның кейбір үлгілерін (моделін) анықтайтын байланыстар

1. Идеалды сығылмайтын сұйықтық:

, (1.63)

мұндағы ішкі энергия тығыздығы - температураның берілген функциясы, қысым, 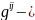тензордың метрикалық құраушылары.

2. Идеалды сығылғыш сұйықтық немесе газ:

(1.64)

мұндағы , – берілген функциялар.

3. Сығылмайтын тұтқыр сұйықтық:

,

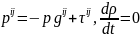(1.65)

мұндағы және – берілген функциялар, тензордың құраушылары тұтқыр кернеулердің тензорлары деп аталады.

4. Сығылатын тұтқыр сұйықтық немесе газ:

(1.66)

мұндағы , – берілген функциялар.

Әдетте, сұйықтық сызықты-тұтқыр (ньютондық) деп аталады егер деформация жылдамдығының тензоры және тұтқырлықты кернеу арасындағы байланыс сызықты болса, яғни

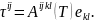
Мысалы, сұйықтың сызықты-тұтқырлы изотропы үшін Навье-Стокстың заңы дұрыс келеді:

(1.67)

мұндағы λ, μ – тұтқырлық коэффициенттері, λ= λ(T), μ= μ(T).

Идеалды немесе тұтқыр, жетілдірілген газ деп аталады, егер

p=RρT, u= R = const = , (1.68)

мұндағы R₀ - универсал газ тұрақтысы, m – газдың молекулалық салмағы.

5. Серпімді (термосерпімді) орта:

мұндағы , - берілген функциялар; - деформация тензорасының құраушылары.

Аздаған деформациясы бар сызықты изотропты термосерпімді орта үшін Гук заңы орындалады, температуралық кернеулерді есепке ала ортырып мынадай түрге ие болады:

(1.70)

ішкі энергия тығыздығы u мына теңдікпен анықталады:

(1.71)

мұндағы ; λ, μ – Ламе коэффициенттері; α – жылудың сызықтық ұлғаю коэффициенті, ϲ – өзгеріссіз деформация процесіндегі меншікті жылусыйымдылық.

Аталып өткен модельдерде (үлгілерде) кернеу тензоры симметриялы деп есептеледі.

Ақпараттар теориясы және термодинамиканың екінші заңы, ретті және ретсіз құрылымдар

Кез келген тірі және өлі жүйе болсын, жинаудың, өңдеудің, түрлендірудің және белгілі бір нысанға бағытталған әрекетті іске асыру үшін ақпаратты таратуды жүзеге асыру процесі кибернетикалық құрылым (машинаның) деп аталады. [6,7].

Бастапқы күйде мұндай құрылым белгісіздіктерге (анықталмаушылықтарға) толы болады. Анықталмаушылықтың тәртібінің мағынасы өте терең. Құрылым іске қосыла бастаған кезде орнықтырып – энтропияны төмендететін ақпарат келіп түседі. Әртүрліліктің азаюы реттеудің негізігі әдістерінің бірі болып табылады.

Тұрақты емес тепе-теңдік күйде тұрған биологиялық жүйелер өзімен қоса жоғары анықталмаушылыққа ие болатын, ықтималдылығы аз құрылымды ұсынады. Кеңістікті-уақыт құрылымдарының болуы – барлық жалпы және материяның фундементальды қасиетіне ие. Реттеу процестері ақпараттар бірліктері мен операциялық басқару элементтері болып табылатын құрылымға ие бола алады.

Құрылымның маңызды мысалы ретінде кейбір жүйелердің кеңістіктің мүмкін болатын күйлерін қарастырамыз[6].

Алдымен көптеген дискретті шекті күйлерді қарастырамыз X_i мұндағы i=1,…..N.

, - ықтималдық күйі X_i , болсын.

P_iықтималдығы – анықталу немесе анықталмау жағдайының X_i шегі.

Больцман-Планк заңына сәйкес жүйенің статистикалық энтропиясы анықталудың(анықталмаушылықтың) математикалық күтімі ретінде анықталады[6].

, (1.72)

мұндағы k=1,381*10^-23 ДжК^-1 – Больцман тұрақтысы.

. (1.73)

Шеннон ақпараттық энтропияны мына теңдеу жүйесімен анықтаған:

(1.74)

Н шамасы – ақпарат шегі, қандай жағдайдың орныққанын анықтап болғаннан кейінгі алатын шамамыз. Әдетте b=2 деп алады немесе ақпаратты бит негізінде өрнектейді.

(1.75)

(1.72), (1.73) формулаларын (1.74), (1.75) формулаларымен салыстыра отырып, біз Больцман-Планктың және Шенноннын энтропиялары өзара пропорционал екенін көреміз:

(1.76)

Жүйенің 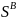статистикалық энтропиясы жүйенің ретсіз шегі ретінде және ұйымдастырылған құрылым шегінде бірге мағыналыланылады.Бұған қоса статистикалық энтропияның максимум шамасы (біркелкі үлестірілуі(таратылуы)) төменгі деңгейлі ұйымдастырылуға сәйкес келеді.

Үзіліссіз жүйелердің көп жағдайларымен ықтималдылық тығыздығы, яғни – ықтималдылық күйі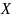 , dX интервалда ұстап тұрады.

Статистикалық энтропия, Больцман мен Гиббстің заңына сәйкес мына формуламен анықталады:

(1.77)

Статистикалық энтропия аддитивті қасиетке ие:

. (1.78)

Клаузиус енгізген термодинамикалық энтропияны статистикалық энтропиямен теңдестіруге Больцман үшін аддитивті қасиет негіз болды. Энтропия жүйенің энергиясына U, көлеміне V, моль санына n_i, құраушыларына i=1,2,…n тәуелді болатын экстенсивті функция күйі сияқты анықталады

(1.79)

Және төмендегідей қасиеттерге ие болады:

1. Жүйенің энтропияның екі ішкіжүйесіне S₁,S₂ бөлінуі кезінде аддативтің ережесі былай орындалады:

S = S₁ + S₂(1.80)

2. Арақатынасы тепе-тең:

(1.81)

мұндағы температура , қысым , химиялық потенциал күйдің қарқынды параметрлері деп аталады.

3. Кез келген күйдің өзгерісі кезінде энтропия өзгерісін екі бөлікке бөлуге болады:

S + S, (1.82)

мұндағы 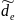S – энергиянын, заттың, сыртқы ортамен ақпараттың алмасуы есебінен энтропия өзгерісі; S – ішкі жүйенің өзінің процестерінің нәтижесінде энтропия өзгерісі.

4. Теңсіздік әрқашан әділ

S (1.83)

Қайтымды процестер үшін

S (1.84)

Ал нақты (қайтымсыз) процестер үшін

S (1.85)

Жылу, зат, ортамен ақпарат алмасуы жоқ жүйелер тұйық жүйелер деп аталынады.

Тұйық жүйелер үшін

S dS = S . (1.86)

Тұйық жүйенің энтропиясы төмендей алмайды. Термодинамикалық күйінің тепе-теңдігі энтропияның максималды мәнімен сипатталды сипатталады:

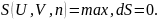
Максималды энтропия дегеніміз ұйымдастырылудың төменгі деңгейін және берілген шарттарда (энергия, көлем, масса) болуы мүмкін ретсіздіктің көп мөлшерін білдіреді. Бұдан салыстырмалы түрде жоғары тындырымдылық жағдайлар тепе-тең емес болуы керек екендігі шығады.

(1.72) формуласына сәйкес тындырымдылық күйінің жоғарғы деңгейі жүйе энтропиясының төмендеуіне алып келеді. Термодинамикалық көз қарас бойынша берілген жағдайда жүйенің бар болуы қолайлы емес.

Мұндай жағдайда берілген шарттағы термодинамикалық тепе-теңдік ең үлкен ретсіздіктің дәрежесіне сәйкес келеді. Осы жағдаймен байланысты жоғары ұйымдастырушылық күй салыстырмалы түрде тепе-тең емес болуы керек.

Барлық тепе-тең емес процестер үшін термодинамиканың екінші заңын қолданған дұрыс

S ,

тепе-тең емес күй үшін:

Тепе-тең емес күй тепе-тең күйге қарағанда жоғары ұйымдастырушылық қасиетке дегенді білдіреді.

Тепе тең емес жүйелерде энтропия орнына энтропия өңдеуі қарастырылады.

(1.14) ескере отырыпP шамасы барлық қайтымсыз процестер үшін оңды болады.