1.6 Гипстің тепе- теңдігі және диссипоция теңсіздігі

Екінші заңы (1.52) және бірінші заң теңдеулерін жылу ағысы теңдеуі түрінде ( 1.44) үйлестіріп қайтымды процесс ортасы үшін келесі қатынасты алыуға болады

du=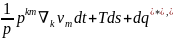 (1.53)

кез-келген процессте өзара тек ортаның ішкі параметрлерімен байланысты (егер 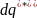=0 ) сыртқы әсерлер ( сыртқы күш жұмысы және жылу ағысы) кинетикалық теңдеуі және термодинамиканың екінші заңы көмегімен ерекшеленген.

Термодинамиканың бірінші және екінші заңының қайтымсыз процесстер болған жағдайда теңдік ( 1.53) орнына теңсіздік алынады (1.43),(1.50) келесіні береді

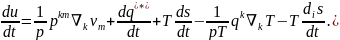(1.54)

Термодинамиканың екінші заңына сәйкес d_is ≥0 сондықтан

du-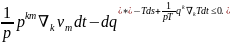 (1.55)

(1.55) формула Клаузиус теңсіздігі ( диссипация теңсіздігі ) деп аталады.

Қайтымды механикалық процессті ортаның мысалы идеалды ( тұтқыр емес ) сұйықтық болып табылады.Анықтама бойынша идеалды сұйықтықта 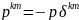(p- қысым) .

=0 кезінде идеалды сұйықтар үшін қатынас (1.53) келесідей

du= 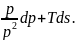(1.56)

Тұтқыр сұйқтық қозғалыс қайтымсыз процесстің мысалы болып табылады.

Тұтқыр сұйыққа

,

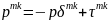Мұндағы = – деформация жылдамдығы , 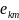тензор компонетінің функциясы болып табылатын тұтқыр кернеу кезінде 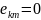тең.

Егер тұтқыр сұйықтар үшін келесі қатынастар орындалса

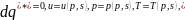
онда теңсіздік ( 1.56) келесі түрде жазылады.

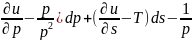
( dt≤0.

аз , 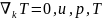мына шамаларда тәуелсіз ds, dp, ескеріп 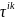аз мәнде аз, болатын процесстерді қарастырып теңсіздік ( 1.56) орындалуы мүмкін деп аламыз, егер

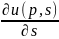T= . (1.57)

Шындығында теңдік (1.57) яғни тек аз мәнінде және 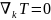кезінде ғана емес барлық процесстер үшін дұрыс.

(1.57) қатынасын ескеріп диссипация теңсіздігін келесі түрге келтіреміз

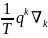- T+ (1.58)

ал (1.55) теңдеуін

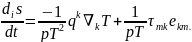(1.59)

(1.59) теңдеу тұтқырлық және жылуөткізгішпен байланысты қайтымсыз процесстер әсерінен тұтқыр жылуөткізгіштік сұйықтарда энтропия өндірісі жылдамдығына арналған теңдеуді береді.

(1.57) теңдеуін қатынас түрінде жазуға болады

du=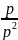 dp+ Tds, (1.60)

бұл формула тек идеалды ғана емес, тұтқырлы сұйықтар үшін де дұрыс және гиббс тепе – теңдігі деп аталады.Оның мәні қайтымсыздықты анықтайтын параметрлерге тәуелсіз термодинамикалық параметрлер арасында қайтымсыз процесстер болған жағдайда да қайтымды процесстегідей болып қалуында.Ұқсас гиббстің тепе – теңдігін басқа тұтас орта үлгілері үшін де жазуға болады.