
- •1.Қатты дене
- •2. Сұйық дене
- •3.Газ тәрізді дене
- •1.2. Механикалық кернеуден болатын деформация
- •1.3. Деформациялану жылдамдығы, ротор.
- •1.4. Механиканың бірыңғай ортасы үшін жалпы заңдылықтар мен теңдеулер
- •1.5 Тұтас орта термодинамикасының заңдары.
- •1.6 Гипстің тепе- теңдігі және диссипоция теңсіздігі
- •1.7 Онзагер принципі
- •1.8. Еркін (бос) энергия, энтальпия, Гиббстің термодинамикалық потенциалы
- •1.9. Тұтас ортаның кейбір математикалық моделі (үлгісі)
- •1.11. Ашық жүйелердің термодинамикасы
- •2.1. Адамның қарқынды қозғалмалы жүйесінің құрылымы
- •2. 5 Сурет. Бас сүйек жазықтығының сагиттальды иінтірегі [5]
- •2. 6 Сурет. Табан мен оған әсер ететін күштер бейнеленген.
- •2. 6 Сурет. Аяқтың ұшымен тұру [5]
- •2. 7 Сурет. Білек пен оған әсер ететін күштер бейнеленген.
- •2. 7 Сурет. Білек сүйектері, тіректі ұстап тұруы
- •2.2. Жердің ауырлық даласында екі аяқпен жүру кезінде дене массасының қозғалыс орталығы
- •2.8 Сурет. Масса орталығының бір қадамға өзгергендегі жүрген жолы
- •2. 3. Дөңгелек жүріс кезінде аяқтардың динамикасын теңестіру, қозғалыстың кезеңдері бойынша талдау
- •2.9 Сурет. Екі аяқты жүйенің моделі
- •2.4 Тұрақты әрекетсіз циркуль жүрісіне сипаттама
- •2.5 Бір периодтық жүріс кезіндегі төзімділік параметірлерін анықтау
- •2.14. Негізгі жалпы теория негізіндегі жүйенің биомеханикалық қозғалысы тепе-теңдікті қалыптастыру
- •2.15. Қозғалыс теңдеуін құратын көпзвеналық динамикалық жүйенің Лагранж формализмін қолдана отырып, деформацияланған элементтер құрылымы
- •2.16. Биомеханикалық бұрандама қозғалыс жүйесі бар, деформацияланған элемент құрылысының теңдеуі мен моделі
- •2.27 Сурет. Жазық қозғалысының бұрандама механикалық жүйесі мен бір тірек фазадағы өзгертілетін геометриялық буын моделі
- •2.17. Механикалық жүйелер элементтердің серпімді модулін анықтау
1.5 Тұтас орта термодинамикасының заңдары.
Термодинамиканың бірінші заңы –энергияның сақталу заңы: әрбір термодинамиканың жүйесінде жүйе күйінің белгілі функциясы – энергия Е бар, жүйеде өтетін процесстің әрбір интервалы үшін теңдік орындалады
dE= A(e)
+
Q(e)
+
A(e)
+
Q(e)
+ **,
(1.37)
**,
(1.37)
Мұндағы dE – энергиядифференциалы, оң жақтағы шамалар дифференциалды емес ; A(e) -сыртқы күштің жұмысы ; Q(e) – жүйе сыртындағы жылу ағысы ; **- уақыт ішіндегі энергияның мүмкін болатын басқа ағыстары.
Кинетикалық энергия Екин өзгеруі тірі күштердің теоремасымен анықталады:
dEкин= A(e)+ A(i), ( 1.38)
мұндағы A(i) – ішкі күштіңжұмысы.
(1.37) , (1.38) формулалары салдары жылуағысының теңдеуі болып табылады.
dU=- A(i)+ Q(e)+ **, (1.39)
мұндағы ( анықтама бойынша) U=E-E кин– ішкі энергия .
Сыртқы нормамен шектелген бетті ∑ тұтас ортаның жеке көлемі V үшін келесі теңдікті жазуға болады.
Eкин
= dV
, U=E-E кин,
dV
, U=E-E кин,
A(e)= pdtdV+
pdtdV+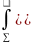 n
n dtdS,
Q(e)
=
dtdS,
Q(e)
=
 массdV
-
массdV
-
 n
dtdS,
n
dtdS,
**= **массdV - n**dtdS.
Мұндағы u– ішкі энергияның тығыздығы ( бірлік шамасының ішкі энергиясы) dqмасс– жылудың массалық ағысы, яғни ішкі нүктеге V тікелей түскенде ;qn - беттік ауданның бірлігі арқылы уақыт бірлігінде нормаль бағытына бет ∑ арқылы түсетін жылу мөлшері ;dq**масс ,qn*- макроскопиялық күштер жұмысы және жылудан бөлек мүмкін болатын энергия түрлерінің сәйкес ағыстары.
Кейін қысқарту үшін dQ** энергияның қосымша ағысы деп айтатын боламыз.
Термодинамиканың бірінші заңын (1.37) келесідей жазамыз
 dV=
)pdV+
n
dV=
)pdV+
n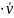 )d
+
)d
+
+ pdV-
pdV- d
+
d
+ (1.40)
(1.40)
(1.40) формуласынан қозғалыс жұмсақ функциясы болып суреттелетін аймақта тұтас орта үшін келесідей энергияның дифференциалдық теңдеуі шығады :
 (
( +u) = (
+u) = ( +
+ -
- ,
,
Мұндағы =
= –
жылу
ағысының
–
жылу
ағысының
 және
қосымша
энергия
ағысының
**;
және
қосымша
энергия
ағысының
**; –векторларының
компонеттері
Умов
– Пойтинганың
энергия
ағысының
тығыздығының
векторы.
–векторларының
компонеттері
Умов
– Пойтинганың
энергия
ағысының
тығыздығының
векторы.
Тірі күштердің теңдеуі (1.38) келесіні береді
(
)(
+
формула (1.39) жылу ағысының дифференциалдық теңдеуіне келтіріледі
 =-
=- +
+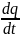 +
+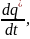 (1.43)
(1.43)
мұнда
dq= –
– бірлік
массаға
жылудың
толық
ағысының
тығыздығы
;
бірлік
массаға
жылудың
толық
ағысының
тығыздығы
;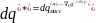 -
қосымша
энергияның
толық
ағысы.
-
қосымша
энергияның
толық
ағысы.
Шама
 (1.44)
(1.44)
бірлік уақытта бірлік массаға ішкі беттік күштің жұмысының теріс белгісімен алынған шама болып табылады.Бұл процессте температура өзгеруіне байланысты масса бірлігіне жылу ағысының шамасының қатынасы меншікті жылу сыйымдылық деп аталады. Жылу сыйымдылық шамасы мұндағы жүретін процесстің және материалдың физико-механикалық қасиетіне тәуелді.
Изотропты денелерге арналған Фурьенің жылу өткізгіштік заңы
 (1.45)
(1.45)
Мұндағы
 – жылу өткізгіштік коэффициенті ; Т-
температура.
– жылу өткізгіштік коэффициенті ; Т-
температура.
Анизотропты орта үшін Фурий заңы келесідей
 (1.46)
(1.46)
мұндағы – жылуөткізгіштік тензор компонеттері.
– жылуөткізгіштік тензор компонеттері.
Егер кез – келген элементарлы бөлшектер үшін жылу ағысы 0-ге тең болса, яғни dq=0 процесс адиобатты деп аталады.Егер температура уақыт бойынша сақталатын болса , яғни dT/dt=0 процесс изотермиялық деп аталады.
Термодинамиканың екінші заңы әрбір термодинамикалық жүйе үшін жүйенің күйі функция – энтропия S болатынын дәлелдейді, жүйеде өтетін процесстің кез –келген аз интервалы үшін келесі қатынас орындалады.
dS= S ,
S ,
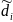 S≥0 (1.47)
S≥0 (1.47)
Мұндағы
dS – энтропия
дифференциялы
;
S - дифференциялды
емес,
келесі
мағынадағы
шексіз
аз
шамалар;
 - сырттағы
энтропия,
S - егер
процесс
қайтымсыз
болғанда
өтетін
жуйедегі
энтропия
өндірісі;
қайтымды
процесстер
үшін
S=0
- сырттағы
энтропия,
S - егер
процесс
қайтымсыз
болғанда
өтетін
жуйедегі
энтропия
өндірісі;
қайтымды
процесстер
үшін
S=0
Егер процессте сол күйінің қайтымды жаққа өткізуге болатые болса, процесс қайтымды деп аталады, яғни тура және кері процесстерде жүйенің барлық бөлшектері үшін бүкіл форма сыртындағы энергия ағысы тек белгісімен ерекшеленеді.Қайтымды процесстер уақыт белгісінің салыстырмалы өзгеруіне инвариантты теңдеуімен сипатталады.Сыртта энтропия ағысы егер жүйе қоршаған ортамен , энергия мен немесе массамен алмасқан жағдайда жүруі мүмкін.
Егер
қоршаған
ортамен
масса
алмасуы
болмаса,
жүйенң
барлық
бөлігіндегі
температура
бірдей
 .
.
Мұндай жүйелерде қайтымды процесс үшін термодинамиканың екінші заңы келесідей
dS= (1.48)
(1.48)
Тұтас
ортада
әрбәр
нүктенің
т
әдетте
әр
түрлі
, ал
жеке
көлемге
V жылу
оның
қабырғалары
∑ арқылы
кіруі
мүмкін.Бұдан
беттің
d
әрбір
элементіне
жылу
(-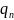 dtd
dtd түседі
немесе
көлем
нүктесіне
тікелей,
көлемге
dV элементіне
түседі
pdqмасс
dV.
түседі
немесе
көлем
нүктесіне
тікелей,
көлемге
dV элементіне
түседі
pdqмасс
dV.
Жылу ағысы есебінен барлық көлемге V сыртқы энтропия ағысы келесідей көрсетуге болады
 dtd
+
dtd
+ dV. (1.49)
dV. (1.49)
Қоршаған ортамен масса алмасу болмаған жағдайда ( дифференциалдық есебінен) тұтас ортының жеке көлемі V үшін термодинамиканың екінші заңын келесідей жазамыз
 dV
,
dV
,

мұндағы S– энтропияның тығыздығы ( бірлік масса энтропиясы) ; dis/dt– жүйедегі энтропия тығыздығы өндірістің жылдамдығы.
(1.49) формуладан үздіксіз қозғалыс үшін энтропия тығыздығының өндірісін сипаттайтын дифференциалдық теңдеу алынады, егер dis/dt :
 , ,
(1.50)
, ,
(1.50)
Термодинаимканың екінші заңының теңдеуін (1.47) келесідей жазуға болады
Tds=
dq+ ,
(1.51)
,
(1.51)
мұндағы
dq=dqмасс
-
 dt;
dt;
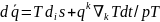 ;
шамасы
компенсирленбеген
жылу
болып
табылады.
;
шамасы
компенсирленбеген
жылу
болып
табылады.
Егер
жылу
өткізгіштік
заңы
басқа
мүмкін
болатын
қайтымсыз
процесстерден
тәуелсіз
болатын
болса,
онда
 шамасы
жылу
өткізгіштен
басқа
барлық
қайтымсыз
процесстер
әсерінен
энтропия
өндірісінің
тығыздығына
тең
және
термодинамиканың
екінші
заңы
бойынша
теріс
емес
болып
табылады.Қайтымды
процесстер
үшін
=0.
шамасы
жылу
өткізгіштен
басқа
барлық
қайтымсыз
процесстер
әсерінен
энтропия
өндірісінің
тығыздығына
тең
және
термодинамиканың
екінші
заңы
бойынша
теріс
емес
болып
табылады.Қайтымды
процесстер
үшін
=0.
Механикалақ процесстер қайтымды болып есептелетін орта үлгілері үшін, мысалы идеалды ( тұтқыр емес) сұйықтар және газдар, серпімді денелер үшін термодинамиканың екінші заңының теңдеуін келесідей жазамыз.
Tds=dq, (1.52)
егер жылуөткізгіштен басқа мүмкін болатын қайтымсыз процесстер ( қайтымсыз химиялық реакция, электрлік тоғының өтуі және т.б. ) болмаса.
