
- •1.Қатты дене
- •2. Сұйық дене
- •3.Газ тәрізді дене
- •1.2. Механикалық кернеуден болатын деформация
- •1.3. Деформациялану жылдамдығы, ротор.
- •1.4. Механиканың бірыңғай ортасы үшін жалпы заңдылықтар мен теңдеулер
- •1.5 Тұтас орта термодинамикасының заңдары.
- •1.6 Гипстің тепе- теңдігі және диссипоция теңсіздігі
- •1.7 Онзагер принципі
- •1.8. Еркін (бос) энергия, энтальпия, Гиббстің термодинамикалық потенциалы
- •1.9. Тұтас ортаның кейбір математикалық моделі (үлгісі)
- •1.11. Ашық жүйелердің термодинамикасы
- •2.1. Адамның қарқынды қозғалмалы жүйесінің құрылымы
- •2. 5 Сурет. Бас сүйек жазықтығының сагиттальды иінтірегі [5]
- •2. 6 Сурет. Табан мен оған әсер ететін күштер бейнеленген.
- •2. 6 Сурет. Аяқтың ұшымен тұру [5]
- •2. 7 Сурет. Білек пен оған әсер ететін күштер бейнеленген.
- •2. 7 Сурет. Білек сүйектері, тіректі ұстап тұруы
- •2.2. Жердің ауырлық даласында екі аяқпен жүру кезінде дене массасының қозғалыс орталығы
- •2.8 Сурет. Масса орталығының бір қадамға өзгергендегі жүрген жолы
- •2. 3. Дөңгелек жүріс кезінде аяқтардың динамикасын теңестіру, қозғалыстың кезеңдері бойынша талдау
- •2.9 Сурет. Екі аяқты жүйенің моделі
- •2.4 Тұрақты әрекетсіз циркуль жүрісіне сипаттама
- •2.5 Бір периодтық жүріс кезіндегі төзімділік параметірлерін анықтау
- •2.14. Негізгі жалпы теория негізіндегі жүйенің биомеханикалық қозғалысы тепе-теңдікті қалыптастыру
- •2.15. Қозғалыс теңдеуін құратын көпзвеналық динамикалық жүйенің Лагранж формализмін қолдана отырып, деформацияланған элементтер құрылымы
- •2.16. Биомеханикалық бұрандама қозғалыс жүйесі бар, деформацияланған элемент құрылысының теңдеуі мен моделі
- •2.27 Сурет. Жазық қозғалысының бұрандама механикалық жүйесі мен бір тірек фазадағы өзгертілетін геометриялық буын моделі
- •2.17. Механикалық жүйелер элементтердің серпімді модулін анықтау
1.2. Механикалық кернеуден болатын деформация
 .
і= 1,2,3 деп есептеп – жүйе координаталар
базисін,
.
і= 1,2,3 деп есептеп – жүйе координаталар
базисін,
 қозғалыс заңы,
қозғалыс заңы,
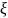 – бөліктердің Лагранждық координаталары,
бастапқы кезедгі қалпында тұрған
координата кеңістігі.
– бөліктердің Лагранждық координаталары,
бастапқы кезедгі қалпында тұрған
координата кеңістігі.
Деформация әдісі ретінде Грин механикалық кернеу болатын деформациясын қолданады [2]:
 (1.10)
(1.10)
Сонымен қатар Альманс деморциясын қолданамыз:
 (1.11)
(1.11)
Мұндағы
 )
– t
)
– t
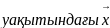
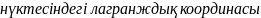 .
.
 (1.12)
(1.12)
Қарапайым көлемнің сәйкес өзгерістері
 (1.13)
(1.13)
Бұнда
 –
тензордың сәйкес нұсқамасы;
–
тензордың сәйкес нұсқамасы;
![]() қайталанатын
индекстер қосылып суммаланып отырады.
қайталанатын
индекстер қосылып суммаланып отырады.
Лагранж сипаттамасы бойынша вектордың орын алмастыруын көрсетейік:
 (1.14)
(1.14)
Сонымен қоса Эйлер сипаттамасы бойынша
 (1.15)
(1.15)
Мұнда

Онда Тензор деформациясы келесідей формуламен есептеледі:
 (1.16)
(1.16)
 (1.17)
(1.17)
Ал кіші деформацияға байланысты келесідей формуламен есептеледі:
 (1.18)
(1.18)
 (1.19)
(1.19)
Диогоналді
элементі
 немесе
немесе
 осьтік
координат аймағында ұзартуды, қысуды
анықтайды,
осьтік
координат аймағында ұзартуды, қысуды
анықтайды,
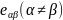 немесе
немесе
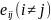 қазіргі кезең уақытындағы материалды
элементтердің арасындағы бұрыштардың
жартысының өзгеруімен байланысты.
қазіргі кезең уақытындағы материалды
элементтердің арасындағы бұрыштардың
жартысының өзгеруімен байланысты.
1.3. Деформациялану жылдамдығы, ротор.
Ортаның
математикалық деформациялануы екінші
рангтің тензорымен анықталады
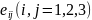 . Көп орталар оның жылдамдыққа әсер
еткен сияты деформацияға әсер етпейді.
Мысалы, бұлшық еттер мен қан. Деформациялаудың
жылдамдығын анықтау үшін деформацияның
тензор жылдамдығы қажет, ол v жылдамдығы
бойынша формуланы көрсетеді.
. Көп орталар оның жылдамдыққа әсер
еткен сияты деформацияға әсер етпейді.
Мысалы, бұлшық еттер мен қан. Деформациялаудың
жылдамдығын анықтау үшін деформацияның
тензор жылдамдығы қажет, ол v жылдамдығы
бойынша формуланы көрсетеді.
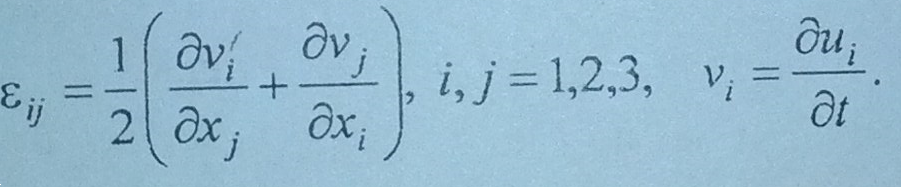 (1.20)
(1.20)
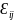 компонентің
механикалық мағынасы келесі де анықталады:
компонентің
механикалық мағынасы келесі де анықталады:
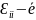 векторы
бойынша бағытталған материалдық
элементтің салыстырмалы ұзару жылдамғы
векторы
бойынша бағытталған материалдық
элементтің салыстырмалы ұзару жылдамғы
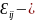 қазрігі
момент уақыты бойынша бағытталған
материалдық элементтердің арасындағы
бұрыштың өзгеру жылдамғының жартысы.
Деформация жылдамдығының тензор
компоненті арқылы таза ортаның көлем
элементін өзгертудің салыстырмалы
жылдамдығында көрсетуге болады
қазрігі
момент уақыты бойынша бағытталған
материалдық элементтердің арасындағы
бұрыштың өзгеру жылдамғының жартысы.
Деформация жылдамдығының тензор
компоненті арқылы таза ортаның көлем
элементін өзгертудің салыстырмалы
жылдамдығында көрсетуге болады
 (1.21)
(1.21)
Ротор векторы (Вихря ) келесі формуламен анықталады.
 (1.22)
(1.22)
Және ол қатты дене сияқты қарастырып отырған көлемнің бұрыштық жылдамдығының айналуын көрсетеді.
1.4. Механиканың бірыңғай ортасы үшін жалпы заңдылықтар мен теңдеулер
Бірыңғай дефоормацияланатын (қатты дене, сұйық және газ ) орта үшін жалпы физикалық заңдылықтар қолданылады, сақтау және бірыңғай ортаның жылдамдығын қалыпын сипаттайтын теңдеулер орындайды.
Ньютон механикасында бірыңғай орта үшін орындар бар:
Массасы сақтау заңдылығы;
Қозғалыс санын сақтау заңдылығы;
Қозғалыс саны моментінің сақталу заңдылығы;
Энергияны сақтау(Термодинамиканың бірінші заңы);
Энтропияны сақтау (Термодинамиканың екінші заңы).
Бұл заңдылықтар бірыңғай ортаның көлемі үшін жазылған интегралды формула постулат сияқты.
Массаның сақталу заңы және үзісместік теңдеуі
Массаны сақтау заңдылығы: жеке индивидуалды көлем үшін масса тұрақты:
 (1.23)
(1.23)
Мұнда, p- тығыздық, m-масса, V- көлем.
Осы формуладан қарап әрбір жеке нүкте үшін узілместік орны бар екенін аңғарамыз.
Эйлер сипаттамасы бойынша қозғалыс келесідей түрге ие болады:
 (1.24)
(1.24)
немесе
 (1.25)
(1.25)
Ал лагранждық күйде
 (1.26)
(1.26)
немесе

Мұнда, div v лагранждық координаталары арқылы анықталады,
 -
уақыт моментіндегі тығыздық.
-
уақыт моментіндегі тығыздық.
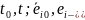 қисықсызықты
ортолардың сәйкес жүйе координаталары.
қисықсызықты
ортолардың сәйкес жүйе координаталары.
Қығылмайтын
орта үшін div
 массаны
сақтау заңдылығы келесідей болады:
массаны
сақтау заңдылығы келесідей болады:
 (1.27)
(1.27)
Қозғалыс санының сақталу заңдылығы: индивидуалды көлемнің өзгергендегі жылдамдығы оған әсер ететін күштер қосындысына тең.
 (1.28)
(1.28)
Мұнда,
ρν –
қозғалыс
саны; F
-
күш;
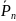 -шекте
берілген күш.
-шекте
берілген күш.
Қозғалысты сақтау заңдылығынан қорыта отырып, кернеу болу керек екенін ескертеді.

1.2- сурет. бірыңғай ортадағы кернеуді анықтау
Тензор кернеуі. Жоғарғы бөлікке әсер ететін күшті сипаттауда, жоғарғы күш тығыздығы вектор кернеуі енгізледі. Ол нормальды аумаққа әсер етеді, оның аумағы ∆S, онда S нөлге ұмтылады.
 (1.29)
(1.29)
Коштың
тензорлық кернеуі p
компоненті
бар
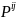 кернеу
векторы бар
тағы да компоненті бар
кернеу
векторы бар
тағы да компоненті бар
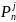 нормалды теңсіздігі бар тензор Р келесі
формуламен анықталады:
нормалды теңсіздігі бар тензор Р келесі
формуламен анықталады:
 (1.30)
(1.30)
Қозғалу санын сақтау заңы бойынша қозғалудың диференциалдық теңдеуі шығады, бұл жерде таза орта келесі фукнция бойынша аныталады:
 (1.31)
(1.31)
Эйлерлік жүйе координаты немесе Лагранждық қосылу жүйесі пайдалану арқылы келесі теңдеуге қол жеткіземіз.
 (1.32)
(1.32)
Бұл
жерде
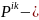 Коши
кернеуінің тензор компоненті;
Коши
кернеуінің тензор компоненті;
 –
жылдамдық векторының компаненті.
–
жылдамдық векторының компаненті.
Қозғалыс санының сақтау ережесі: қозғалыс санының кезеңінің жылдамдығын өзгерту қозғалып тұрған кезеңдердің оған сырттай әсер еткен күш және будың қосындысына тең.
 (1.33)
(1.33)
Бұл
жерде, r – орта нүктесінің радуис векторы;
ρ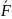 -
ауырлық күштің көлемдік тығыздығы; ρ
-
ауырлық күштің көлемдік тығыздығы; ρ –
қозғалыстың ішкі кезеңгің көлемдік
тығыздығы;
–
қозғалыстың ішкі кезеңгің көлемдік
тығыздығы;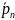 – жоғарғы күштің жоғарғы тығыздығы;
ρ
– жоғарғы күштің жоғарғы тығыздығы;
ρ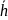 –
массалық бу кезеңінің көлемдік тығыздығы;
–
массалық бу кезеңінің көлемдік тығыздығы;
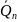 –
массалық бу кезеңінің жоғары тығыздығы.
–
массалық бу кезеңінің жоғары тығыздығы.
n индексі , мәнінде аймақтың орналасуына байланысты формулаға тәуелді екенін көрсетеді. 1.33-шi формуладан кезеңге арналған теңдеу пайда болады.
 (1.34)
(1.34)
Ішкі кезең және ішкі әрекетсіз қозғалыс кезеңнің сақталу заңы Кош тығыздығын пайда болдырады:
 (1.35)
(1.35)
Кезең
кернеуінің тензорын енгіземіз
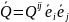 .
Бұл кез келген аймақта қалыпты
.
Бұл кез келген аймақта қалыпты
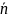 нормалы
келесідей болады
нормалы
келесідей болады
 .
.
Қозғалыс санының ішкі кезеңі болуы ρ ол микроскоптық таза ортаның бөліктерден құралғанына байланысты болады, микроскоптық нөлге теі болса да, олар белгілі кезеңі бар болуы мүмкін.

1.3-сурет 1.4- сурет
Қозғалыс санының ішкі кезеңдері суспензиялар, сұйық кристалдар, магниттік кристалдар, қан болу мүмкін. Таза ортаның басқарма жүйесінде қозғалыс санының ішкі кезеңі бар болса, Қозғалыс моментінің ішкі моментін анықтаушы арнайы теңдеу қосу қажет. Таза ортаның тензор кернеуі қозғалыс санының ішкі кезеңі бар кезде және буының таралаган жағдайда симметриялық болуы мүмкін.
Энегерия сақталу заңы (термодинамиканың I заңы): жеке меншік көлемінің толық энергиясының өзегеру жылдамдығы уақыт бірліігіне келген энергияға тең.
 (1.36)
(1.36)
Бұл
жерде
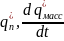 уақытқа
тәеулді пайда болған энергияның жоғары
және салмақтық тығызыдығы .
уақытқа
тәеулді пайда болған энергияның жоғары
және салмақтық тығызыдығы .
Энтропии сақталу заңы ( термодинамиканың екінші заңы ): жазық ортаның жеке көлемінің энтропиясының S өзгеру жылдамдығы көлем ішіндегі энтропия өндірісі және сыртындағы энтропия ағысының бірлік уақыттағы қосындысыны тең.
Көлем ішіндегі энтропия өндірісі теріс емес:
 =
=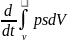 =
=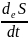 +
+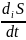 ,
≥0
,
≥0
Мұндағы S – энтропия, бірлік уақыттағы сыртқы көлемге V энтропия ағысы ; - бірлік уақыттағы көлем ішіндегі энтропия өндірісі.
Соңғы көрсетілген екі заң 1.5 тарауында толығырақ қарастырылған.
