
- •1.Қатты дене
- •2. Сұйық дене
- •3.Газ тәрізді дене
- •1.2. Механикалық кернеуден болатын деформация
- •1.3. Деформациялану жылдамдығы, ротор.
- •1.4. Механиканың бірыңғай ортасы үшін жалпы заңдылықтар мен теңдеулер
- •1.5 Тұтас орта термодинамикасының заңдары.
- •1.6 Гипстің тепе- теңдігі және диссипоция теңсіздігі
- •1.7 Онзагер принципі
- •1.8. Еркін (бос) энергия, энтальпия, Гиббстің термодинамикалық потенциалы
- •1.9. Тұтас ортаның кейбір математикалық моделі (үлгісі)
- •1.11. Ашық жүйелердің термодинамикасы
- •2.1. Адамның қарқынды қозғалмалы жүйесінің құрылымы
- •2. 5 Сурет. Бас сүйек жазықтығының сагиттальды иінтірегі [5]
- •2. 6 Сурет. Табан мен оған әсер ететін күштер бейнеленген.
- •2. 6 Сурет. Аяқтың ұшымен тұру [5]
- •2. 7 Сурет. Білек пен оған әсер ететін күштер бейнеленген.
- •2. 7 Сурет. Білек сүйектері, тіректі ұстап тұруы
- •2.2. Жердің ауырлық даласында екі аяқпен жүру кезінде дене массасының қозғалыс орталығы
- •2.8 Сурет. Масса орталығының бір қадамға өзгергендегі жүрген жолы
- •2. 3. Дөңгелек жүріс кезінде аяқтардың динамикасын теңестіру, қозғалыстың кезеңдері бойынша талдау
- •2.9 Сурет. Екі аяқты жүйенің моделі
- •2.4 Тұрақты әрекетсіз циркуль жүрісіне сипаттама
- •2.5 Бір периодтық жүріс кезіндегі төзімділік параметірлерін анықтау
- •2.14. Негізгі жалпы теория негізіндегі жүйенің биомеханикалық қозғалысы тепе-теңдікті қалыптастыру
- •2.15. Қозғалыс теңдеуін құратын көпзвеналық динамикалық жүйенің Лагранж формализмін қолдана отырып, деформацияланған элементтер құрылымы
- •2.16. Биомеханикалық бұрандама қозғалыс жүйесі бар, деформацияланған элемент құрылысының теңдеуі мен моделі
- •2.27 Сурет. Жазық қозғалысының бұрандама механикалық жүйесі мен бір тірек фазадағы өзгертілетін геометриялық буын моделі
- •2.17. Механикалық жүйелер элементтердің серпімді модулін анықтау
2.16. Биомеханикалық бұрандама қозғалыс жүйесі бар, деформацияланған элемент құрылысының теңдеуі мен моделі
Адам қозғалысына максималды жақындатылған он бір буынды адам пішінді модельді қарастырайық. Масса центрінің қозғалысы болып жатқан, біртекті фазаға xyz координатасының бастапқы О нүктесі және xy жазықтығы бар қимылсыз оң және сол жақ декартов жүйесін, биомеханикалық жүйесінің жазық қозғалысын зерттеу үшін енгіземіз.
Жүйеде
2 үшбуынды салмақты аяқтар, 2 екібуынды
с алмақты қолдар мен салмақты корпус
бар. Құрылымның барлық элементтері
серпімді болып келеді, ал бұрандаманың
ұзындығы- уақыт функциясы:
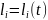 (i=1,
…, 11). 2.27 суретте бұл механизм көрсетілген
және сәйкес белгілер енгізілген.
(i=1,
…, 11). 2.27 суретте бұл механизм көрсетілген
және сәйкес белгілер енгізілген.
2.27 Сурет. Жазық қозғалысының бұрандама механикалық жүйесі мен бір тірек фазадағы өзгертілетін геометриялық буын моделі
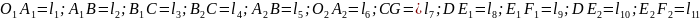 – адамды
модельдейтін биомеханикалық жүйенің
буын ұзындығы болсын. Біртекті фаза
жағдайы бір мәнді
бұрышымен және бұрандама ұзындығы
анықталады. Сондықтан қарастырылған
жүйе 22 дәрежелі еркіндігі бар.
i-нші
шарнирда (i=1,
…, 11) дамитын моментін
– адамды
модельдейтін биомеханикалық жүйенің
буын ұзындығы болсын. Біртекті фаза
жағдайы бір мәнді
бұрышымен және бұрандама ұзындығы
анықталады. Сондықтан қарастырылған
жүйе 22 дәрежелі еркіндігі бар.
i-нші
шарнирда (i=1,
…, 11) дамитын моментін
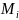 деп белгілейміз.
деп белгілейміз.
Масса
центрі келесі нүктелерде болады:
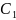 - тірек аяқтың табаны,
- тірек аяқтың табаны,
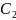 - тірек аяқтың сирағы,
- тірек аяқтың сирағы,
 - тірек аяқтың бөксені,
- тірек аяқтың бөксені,
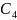 - ауыспалы аяқтың бөксені,
- ауыспалы аяқтың бөксені,
 - ауыспалы аяқтың сирағы,
- ауыспалы аяқтың сирағы,
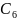 - ауыспалы аяқтың табаны,
- ауыспалы аяқтың табаны,
 -
корпусы,
-
корпусы,
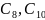 - иықтары,
- иықтары,
 -
иық алды. Олардың жағдайын бастапқысына
сәйкес келетін
-
иық алды. Олардың жағдайын бастапқысына
сәйкес келетін
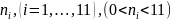 буынды көбейткіштер түрде береміз (егер
барлық буындар сәйкес бұрыштарды индекс
нөмерлері бойынша нөмерленсе).Осындай
тапсырмалар масса центрінің жағдайы,
адамды модельдеудің осы жағдайда
қолданылуы тиімді.
буынды көбейткіштер түрде береміз (егер
барлық буындар сәйкес бұрыштарды индекс
нөмерлері бойынша нөмерленсе).Осындай
тапсырмалар масса центрінің жағдайы,
адамды модельдеудің осы жағдайда
қолданылуы тиімді.
Массалары: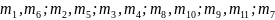 -табандары,
бөкселер, сирағы, иық алды, иықтары және
де корпус. Инерция моменттері:
-табандары,
бөкселер, сирағы, иық алды, иықтары және
де корпус. Инерция моменттері:
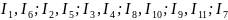 -
табандары, бөкселер, сирағы, иық алды,
иықтары және де корпус. Оң және сол жақ
механизм соңын әр түрлі деп есептейміз.
-
табандары, бөкселер, сирағы, иық алды,
иықтары және де корпус. Оң және сол жақ
механизм соңын әр түрлі деп есептейміз.
Билмеханикалық жүйе қозалысты есептеу әне модельдеу кезінде, барлық келтірілген мінездемелер, сәйкесінше сынап тұрған адамның мінездемесіне тең.
Масса центрінің қозғалыс теңдеуін жазайық:
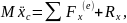
 (2.62)
(2.62)
Мұндағы М- барлық динамикалық жүйенің массасы; - еркін құлау үдеуі; - динамикалық жүйеге бекіту нүктеге тіркелген қосымшаларының, тік және көлденең құрайтын сыртқы күш реакциясы; - динамикаық жүйенің масса центрінің координаталары, оның құрылымымен анықтайтын, олар деформация және буын қозғалыс кезінде өз жағдайын өзгертеді.
Белсенді сыртқы күш жоқ, сондықтан қозғалыс ішкі күштің және сыртқы күштің реакцияның әсері арқылы болады.
(2.51) теңдеулері үшін бастапқы шарттар:
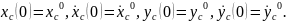 (2.63)
(2.63)
(2.55), (2.58) формулаларды (2.53) орнына қойып, буындардың бұрыштық координатасын (2.64)-(2.75) және бұрандама ұзындық тербелісінің (2.76)-(2.87) өзгерісін суретейтін, адам пішінді он бір буынды механизмді қозғалыстар теңдеулер жүйесін аламыз.
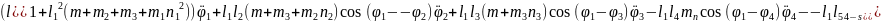
 (2.64)
(2.64)
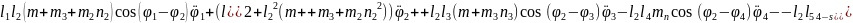
 (2.65)
(2.65)
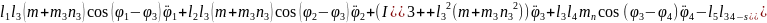
 (2.66)
(2.66)
 (2.67)
(2.67)
 (2.68)
(2.68)
 (2.69)
(2.69)
 (2.70)
(2.70)
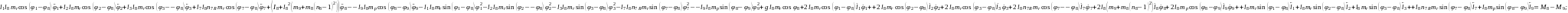 (2.71)
(2.71)
 (2.72)
(2.72)
 +g
+g (2.73)
(2.73)
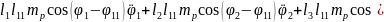
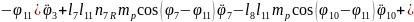
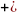
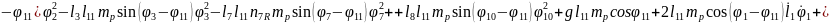
 (2.74)
(2.74)
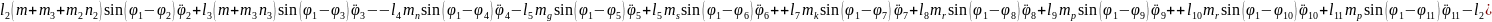
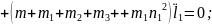 (2.75)
(2.75)
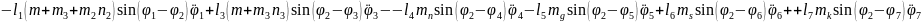

 (2.76)
(2.76)
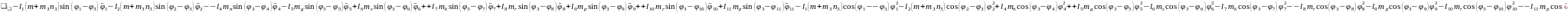 (2.77)
(2.77)

 (2.78)
(3
(2.78)
(3

 (2.79)
(2.79)
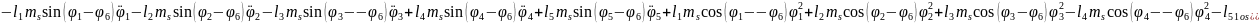
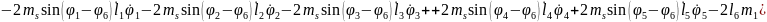 (2.80)
(2.80)

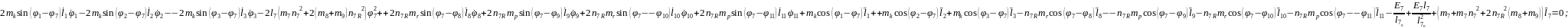 (2.81)
(2.81)
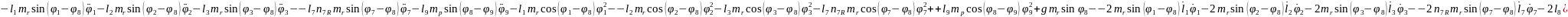 (2.82)
(2.82)
 (2.83)
(2.83)
 (2.84)
(2.84)
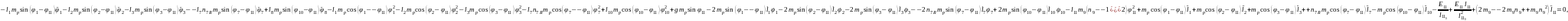 (2.85)
(2.85)
Мұндағы
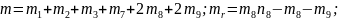
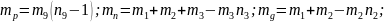
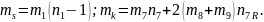
Осылайша, адамның қозғалысын модельдейтін, деформацияланатын құрылым элементтері бар, 11 буынды стерженді биомеханикалық жүйенің стержень тербелісі мен бұрыштық айнымалы өзгерісін сипаттайтын, теңдеулер құрастырылған. Біртіреуішті фазадағы механизм өозғалысының теңдеуі, 22 бейсызықты дифференциалды теңдеулер жүйесін көрсетеді.
Жалпыланған күштерді жазайық:

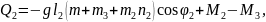
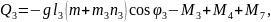

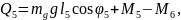



 (2.86)
(2.86)
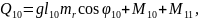
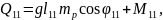

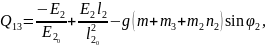
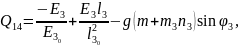


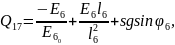
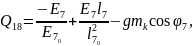

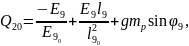


Қозғалыс теңдеулер жүйесінің ортақ шешімі 44 еркін тұрақтыларға тәуелді, сондықтан қозғалысты бірмәнді анықтау үшін, оның бастапқы шартын беру қажет. Бұрыштық координаттар үшін –(2.87), буын ұзындықтар тербелісі үшін –(2.88):
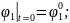
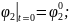
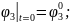
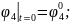

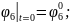
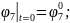

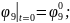
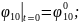
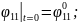 (2.87)
(2.87)
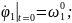

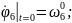
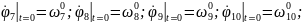
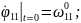

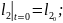
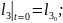
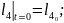

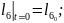


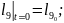
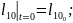
 (2.88)
(2.88)

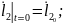
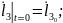
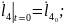


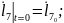
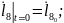


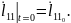
Бастапқы шарттардың жүріске әсері тез жоғалады. Тұрақталған қозғалыс құрастырылады.
Уақыт
кезінде қозғалысты тік құрайтын
реакцияда, шамаларды дұрыстықта болған
үзіліссіз қозғалыстар шарттарды маңызды
тексеру керек. Егер
 болса, қозғалыстың тірексіз фазасы
болады. Онда нөлдік тірек реакциялар
кезіндегі қозғалыстың ортақ массасы
бар теңдеуді осы формулалармен бірге
зерттеу қажет.
болса, қозғалыстың тірексіз фазасы
болады. Онда нөлдік тірек реакциялар
кезіндегі қозғалыстың ортақ массасы
бар теңдеуді осы формулалармен бірге
зерттеу қажет.
Жүріс кезінде кезектес шарттар орындалады:
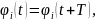 (i=1, …,
11),
(2.89)
(i=1, …,
11),
(2.89)
ал сjнымен бірге қайталану шарттары:
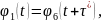


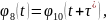
 (2.90)
(2.90)
(екінші
аяқ пен екінші қол алғашқы тура
қозғалыстарды
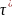 уақытпен кешігіп қайталайды).
уақытпен кешігіп қайталайды).
Биомеханикалық қозғалыс жүйесін сипаттау үшін, адам қозғалыстырына үлгі жасайтын, аяқтардың аусымдары теңдеулері тұйықталған теңдеулер жүйесі қажет. Аяқты тірекке қойған кезде, жылдамдық және үдеу секіріспен өзгереді. Аяқтарды ауыстыру уақыты кезінде, кезекті аяқ жермен жанасуы және тірек аяқтан жерден үзуі болады. Осылайша кезекті аяқ тіректі және керісінше болады.
Кинетикалық момент жұйесінің сақтау шарттарынан аяқтардың аусымды процессін суреттейтін, алгебралық теңдеу жүйесін аламыз:
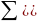 (2.91)
(2.91)
Мұндағы
- сәйкес келетін элементтің массасы;
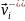 - аяқ ауысқанға дейін момент кезіндегі,
сәйкес келетін элементінің масса
центірінің жылдамдығы;
- аяқ ауысқанға дейін момент кезіндегі,
сәйкес келетін элементінің масса
центірінің жылдамдығы;
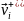 - аяқ ауысқаннан кейін момент кезіндегі,
сәйкес келетін элементінің масса
центірінің жылдамдығы;
- аяқ ауысқаннан кейін момент кезіндегі,
сәйкес келетін элементінің масса
центірінің жылдамдығы;
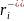 - аяқ ауысқанға дейінгі сәйкес келетін
буындар жағдайын суреттейтін вектор;
- аяқ ауысқанға дейінгі сәйкес келетін
буындар жағдайын суреттейтін вектор;
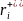 - аяқ ауысқаннан кейінгі сәйкес келетін
буындар жағдайын суреттейтін вектор.
- аяқ ауысқаннан кейінгі сәйкес келетін
буындар жағдайын суреттейтін вектор.
Биомеханикалық жүйесі (буындар саны мен буындардың өзі) нақты түрден шығып, жүйеге кіретін өлшемдер түрі теңдеулер саны арқылы анықталады.
(2.91) формулалар- бұл лездік қойылатын және алынатын теңдеулер жүйесі.
Тербеліс бұрандамалары үшін (2.75)-(2.86) теңдеулерін шешіп, (2.63)-(2.74) жүйесіне қойып, формулалар санын қысқартуға болады.
Берілген есепте деформацияланған қатты денелер сыртқы күштер арқылы емес, ішкі күштер арқылы беріледі. Қатты денелер ішкі күштер әсерінен орнын ауыстыра алмайтыны белгілі, ал деформацияланған жүйелер Жердің қатысуымен және нүктелер бекітуімен орнын ауыстыра алады.
Бұл кезеңде динамиканың тура есептелуі жинақталған - алған теңдеулер негізінде жүріске үлгі жасап, бағалап, қанша шынайы жүрісті көрсететінін, яғни берілген оң жақ бөлігі алынған жүйе теңдеуін шешіп, анықтау керек. Бұл жерде тірі материя және өлі маерияның айырмашылығы пайда болады. Қатты денеде белгілі болып есептеленетін, сыртқы күштер беріледі. Тірі материяда – белгісіз, ішкі күштер. Осы күштер туралы тек жорамал жасауға болады немесе эксперементті түрде анықтауға болады.
Күштер анықтау методикасы 2 бөлімінде жазылған. Моменттерін анықтап, осы шешімдерін теңдеулерде қолданамыз және орындалған процесс жүрісін қарастырамыз. Жүріс критериі- есептелген қозғалыс пен бастапқы жүріс арасындағы айырмашылығы минималды болу керек.
Нақтылы эксперементальді оң бөлікпен дифференциалды теңдеулер жүйе шешімін нәтижелері бойынша, қозғалысты теория жағынан аламыз және адамның бастапқы жүріспен салыстырамыз. Зерттеу нәтижесінде механикалық модельді адам пішінді үлгіге максималды жақындату қажет.
Сонымен қатар динамиканың тура есебі қойылған және оның математикалық тұжырымы берілге, яғни жалпы алғанда түрдегі құрылымнан 11 деформацияланатын элементтермен, динамикалық жүйелер қозғалыстары дифференциалды теңдеулердің тұйықталған жүйені қосып, буындардың бұрыштық орнын ауыстыруын, масса центірінің қозғалысын, буындардың деформациялануын және аяқтардың ауысуын суреттеп, осы теңдеулерден тұрады. Ол үшін теориялық механиканың классикалық талдау және математикалық талдау әдістері қолданылған. Қойылған есептер үшін бұл тұйықталған математикалық тұжырым.
