2.14. Негізгі жалпы теория негізіндегі жүйенің биомеханикалық қозғалысы тепе-теңдікті қалыптастыру

Екі аяқпен жүру – табиғатта сирек кездесетін парадокс. Бұнда ашылмаған сырлар өте көп. Зерттеулер нәтижесі бойынша, жүріс кезінде астынғы бөлікте жылдамдату проццесі болып жатады және оны миға жібереді.

Бірақ та шынайы шарттарға сүйенсек үстінгі бөліктен ондай жылдамдату байқайлмайды. Осыдан қорыта келгенде, қатты моделдер шынайы құбылысқа барабар емес. Тірі табиғатта ең басты орынды демормацияланған жүйе орын алады. Сондықтан биологиялық жүйелерді моделдеу кезінде механиканың демормацияланған денелерін қолдану керек.

Механикадағы деформация ұшан қилы. Демормацияларды есепке алу және деформацияланған жүйелерді есептеу өте қиын, оларды қолдану аясында неше түрлі эффектілерді қолдану мүмкіндігі бар. Мысалы, «энергия соғысы қайда кетеді?» деген сұрақ туындайды. Адам жүріс адам тәрізді роботқа қарағанда үнемдірек. Энергияны рекуперациялау механизмі бар, яғни аяқ ороын ауыстырған кезде соғылудан қорғайды. Итерген кезде немесе орын ауыстырғанда аяқ қаңқа көп энергия жұмсайды. Бұл жағдайды, протез немесе адам тәрізді робот жаағанда есепке алу керек.

Егер тұтқырлықты есепке алсақ, онда кез келген қозғалыс тоқтауға алып келеді. Тұтқырлық аса үлкен жылдамдықта және тездеткенде маңызды орын алады. Ал жай жүріс кезінде үлкен жылдамдық қажет емес, сондықтан тұтқырлық аса маңызды емес, тек қана қатты деформацияны есепке аламыз.

Қатты деформация кезінде тоқтауға алып келетін емес, периодты тербеліске акеледі. Осындай биомеханикалық жүйені сипаттау кезінде қатты демормациялауды есепке ала отырып, жүріс кезінде Лагранж формализмін қолдануға болады.

Деформациян есепке ала отырып, адам қозғалысын моделдейтін биомеханикалық жүйені туындатуға үшін, деформацияланған элементтері бар механикалық жүйені қарастырайық, онда адам қозғалысын зерттейді.

Енді механикады көпзвенолық жүйені қарастырайық, ол он бір звендерден тұрады. Барлық звеньдар инерциялық массадан тұрады, Зеньдер соңғы жағында шариктер арқылы байланысып тұрады. Әрбір байланыста айналy уақыты бар.

Звенаның деформмациялану массасына байланысты өз орнын ауыстыра алады. Орталық массанң орнының өзгеруі звенаның ұзындығының өзгеруңне байланысты. Орталық масса координаталары жүйенің анықталған есептерімен белгілі геометриялық амалдармен қарастырылады.

Қозғалысты басқаруды ұйымдастыра отырып, сонымен қатар реакция күшін анықтау және адам тәрізді механизмдердің жерден аяқты көтеру жүзеге асыруды басқару. Келесі суретте биомеханикалық жүйенінің қарастырған.2.26-сурет.

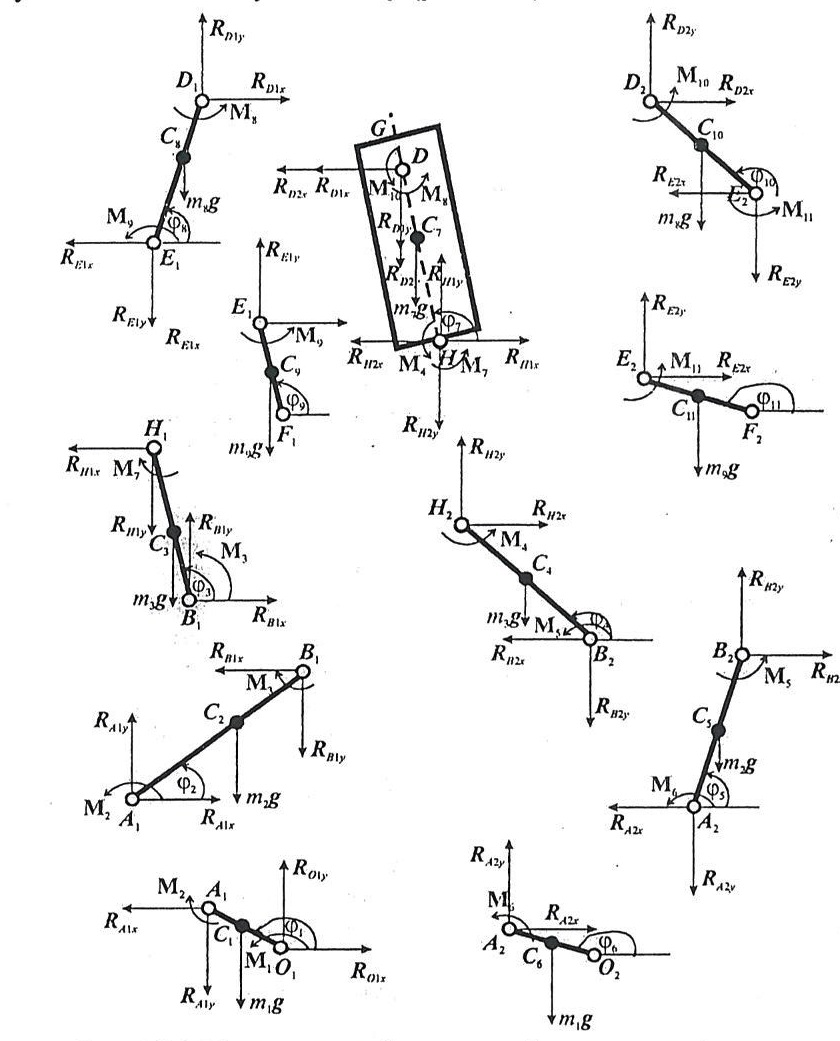
2.26 сур. Бөлінген түрдегі жазық өзекшелі (стержнь) механикалық жүйенің үлгісі

Механизм орталық масса координаталары белгілі геометриялық қатынастармен анықталады, олар туралы айтылмайды. Мәндерді енгізейік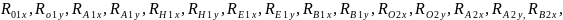

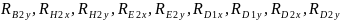, тік және көлденең орналасқан реакция нүктелері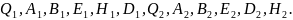

Тіреуші аяқтың табаны үшін орталық масса қозғалысы теориясын және орталық массасына байланысты сәттегі кинетикалық өзгеріс туралы теореманы қарастырамыз:

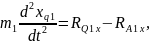
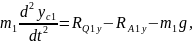
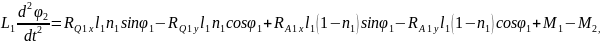
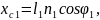
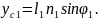2.42

Тіреуші аяқтың жіліншікгі үшін орталық масса қозғалысы теориясын және орталық массасына байланысты сәттегі кинетикалық өзгеріс туралы теореманы қарастырамыз:

,

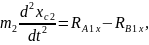
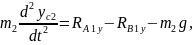
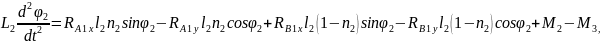
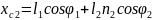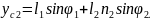2.43

Тіреуші аяқтың жамбасы үшін орталық масса қозғалысы теориясын және орталық массасына байланысты сәттегі кинетикалық өзгеріс туралы теореманы қарастырамыз:

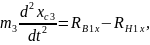
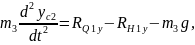
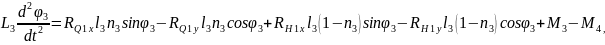
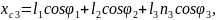
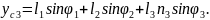2.44

Оң жақ білек үшін орталық масса қозғалысы теориясын және орталық массасына байланысты сәттегі кинетикалық өзгеріс туралы теореманы қарастырамыз:

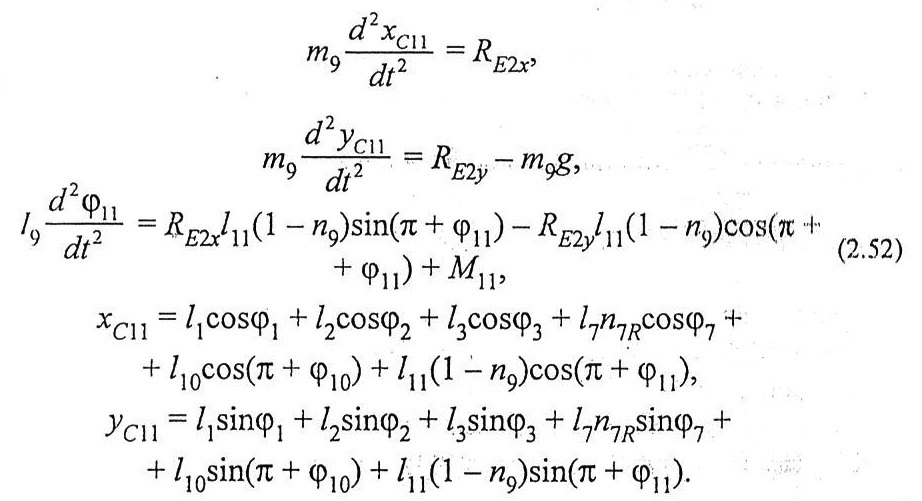
Инерция сәтінің өзгеруіне байланысты білінбейтін күшті сақтаймыз.Орталық масса қозғалысы теоремасы бойынша бірсызықты жүйенің шешімі бойынша шешеміз, олар 22 реакция теңдеулерінен тұрады. Бұл теңдеулерді жазбаймыз, себебі өте үлкен. Табылған реакциялар орталық массаға қатысты кинетикалық өзегрістер теоремасына қойылады. Оларды жеңілдете отырып, өозғалыс теңдеуін аламыз. Оларды жазбаймыз. Лагранж форализминен кейін қорытындылай келе айтамыз.