2.4 Тұрақты әрекетсіз циркуль жүрісіне сипаттама

Есеп барысында, әрекетсіз циркуль жүрісі кезінде екі аяқты жүйе төменгі қиғаш тегістікте тұрақты жылжи алатынын көрсетті.

2.10 сур. Циркульдік екі аяқты жүрісінің фазалық суреті

Жүйенің фащалық кескіні көмегімен пассивті жүрістің орнықтылық үрдісін қарастырайық. Бұл жүйенің фазалық кескіні төртеселік болып табылады. Төртеселік графикалық кеңістікті емес, екіеселік фазалық кескінге шектелеміз. Бұл қысқартылған нұсқа координата мен бір аяқтының жылдамдығын көрсетеді.

2.10 суретте Тұйықталған траеториямен сипатталатың,алғашқы қозулар өшкен тұрақты жүріс кезіндегі жүйенің жағдайы көрсетілген. Бұл жерде симетриялық жүріс қарастырылған, сондықтан өзге аяқпен байланысқан фазалық сурет сондай болу керек. Басқа типті жүрістердің фазалық суретті басқа болады, мысалы 8-периодтық немесе хаостық өзгеше болады.

Суретті зерттеуді , артта орналасқан аяқ жерден жаңадан жерден ажырағанда яғни, переносимой аяққа айналғанда, t=0⁺ моменттік уақытына сай келетің І нүктесінен бастаймыз. Сызуда алдыңғы аяқттын соңғы жағында қара нүктемен жермен байланыс орыны көрсетілген.

Фазалық траектория бойынша қозғалыс сағат тіліне бағыттас жүреді. Вертикальді оспен қиылысу уақытында жүйенін кординатасы вертикальді жағдайда орналасады.ІІ жағдайы t=Т^- сағаттық моментіне сәйкес, бұл уақытты ауыстырылатын жермен тиуі. Ауыстырылатын аяқпен жердің жанасуы t=Т уақыттық моментінде болады. Бұл жанасу кезінде соғылу болады, сол үшін біз ІІ және ІІІ нүктелер аралығында жылдамдық секірісін аламыз.Графиканың үстінгі жағы (І-ІІ) ауыстыру аяғының қозғалысын сипаттайды, оны аяқтары байланыстырушы шарикке ілінген маятниктін қозғалысы сияқты суреттеуге болады.ІІІ кезінде ауыстыру аяқғы тірек аяққа айналады және жермен аяқтың жанасу нүктесімен байланысқан, аяқты кері маятник ретінде сипаттайтың, фазалық траекторияның төменгі бөлігі орындалады. III-V моменттеріндегі жылдамдық секірісі өзге аяқтын жермен жанасуымен байланысты.

2.5 Бір периодтық жүріс кезіндегі төзімділік параметірлерін анықтау

Бірпериодтық немесе симметриялық жүріс мүмкін болатын екі аяқты жүрісті үлгілеу (моделирование) үшін төрт параметр алуымыз керек. Бұл Т жүрісінің периоды,α аяқтар арсындағы максималдық бұрыштың жартысы,сонымен қатар _ns , _s жылдамдықтарының бастапқы белгісі. Басқа параметірлерді осы төртеуінің арқасында есептеп алуға болады. Жүйе қозғалысының сызықтандырылған теңдеуінің шешімі алынды. Тасмалдау(перенос) деңгейлері үшін:

(2.26)

Осы теңдеулерден бұрыштық жылдамдық үшін қөрінісін аламыз:

Сонымен қатар аяқтың ауысуының екі теңдеуін де есепке алған жөн:

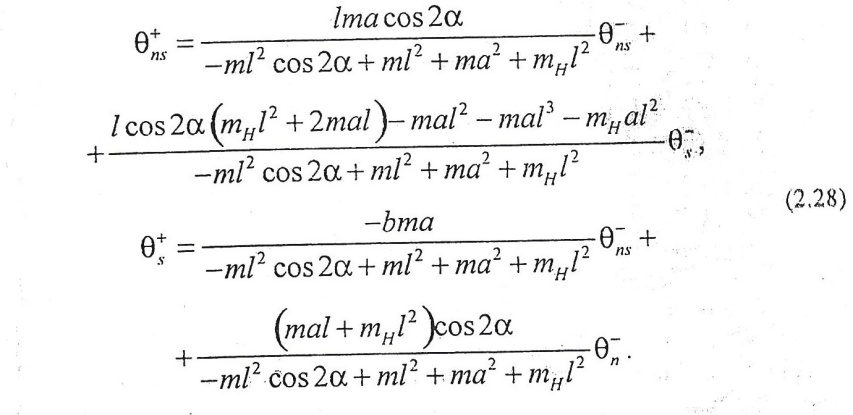
Ө⁺_ns= Ө_ns (0), Ө⁺_s= Ө_n (0) симметриялық жүріс үшін.Симметриялық жүріс соңғы қадамда балық параметрлер бастапқы қалпына келетінің көрсетеді. t=Т деп қабылдап және бастапқы бұрыштарды α және Φ орынына Ө_s, Ө_ns , біз сәйкесінше -α-φ және α-φ коя аламыз. Ө_s, Ө_ns орынына ^-_s, ^-_ns аламыз.Осыдан кейін алынған теңдікті аяқты ауыстыру үшін арналған жылдамдық теңдеуіне қоямыз,бұрыштық(углов) формуламен қоса төрт белгісіздікпен төрт теңдік аламыз. Оларды жүйенің белгілі инерциондық және геометриялық параметрлерде, сонымен катар жазықтықтын бұрыштық еңкейуімен шешіп, екі аяқты жүрісті үлгілеу (моделирование) үшін ізделіп отырған параметрлерді аламыз.

Осы бейсызықты алгебралық теңдеулердің аса қолайсыз үлкендігін айта кеткен жөң. Соған байланысты бастапқы қадам параметрлеріне аналитикалық көрінісін алу қиын.

Өте жоғары қиындықтарға байланысты толық теңдеудің шешімін табу сандық әдіспен жүзеге асады. Толық теңдіктін жақындатылған шешімін алу үшін, сызықты теңдеулерді қолдануға болады.

Екі аяқты жүйе нық, бірпериодтық жүріспен қозғалады, егер Пуанкарда

(2.29)

көрсетілсе, мұнда і- қадам номері.

Ақырында.f (θ^*) = θ^* - қозғалмайтын нүкте бар.

Нықтылықты тексеру үшін келесі функцияны еңгіземіз g (θⁱ)=f (θⁱ) - θ ⁱ.Қозғалмайтын нүктелерге g (θⁱ)=0. Нольдік нүктелерді табу үшін оны Ө^* аумағындасызықтандыруға болады:

(2.30)

мұнда Ө₀ - қозғалмайтың нүктеге бастапқы жақындау; 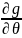- g функциясының якобианының келесі жолмен табамыз:

1. Алдымен Ө₀ (оны g₀ деп аламыз) нүктесінде g есептейміз.

2. Бірінші параметрді Ө және ξ бағанасына қоямыз, g-ды қайтадан есептейміз. Қортындысында келесі формуланы қоолдану арқылы

(2.31)

- бірінші бағананы аламыз.

3. Басқа бағаналарды 2-де көрсетілген жолмен алуға болады.

Якобианды алғаннан кейін Ө₀ жетілдідіру теңдігі келесі көрініс алады

(2.32)

Ө келесі белгісі:

(2.33)

Нық қадамды зерттеуде туатын негізгі мәселелерді қарастырайық:

1. f (θ) функциясының ең киын сипаттамасы. Оны есепту үшін Mathematica 4.0 пакеті қолданылған және ол үшін қадамды басынан соңына дейін үлгілейтін (моделирующая) программа құралған. Соған байланысты Ө_s, Ө_ns нүктелері уақыттық дискретті фуекция болып табылатындықтан, f (θ) есептеу бірнеше кезеңдерден тұрады және жоғарғы дәлдікті қажет етеді. Ол есептің жылдамдығына әсер етеді.

2. Ө₀ бастапқы жақындауы Ө^* әжептеуір жақын болуы тиіс. Көп жағдайда оған жету қиын,тсондықтан іріктеу тәсілін пайдалану кажет.

2.6. Қозғалыс жүйесін орнықтылыққа зерттеу

Екі аяқты жүйесін орнықтылыққа зерттеу кезінде ең біріншіден ескере кететін жағдай оның статистикалық тұрғыдан орнықты емес емес екенін анықтайды, яғни қозғалыс жоқ болса құлауын айтып отыр. Бұл жағдайда тек қана динамикалық орнықтылық мүмкін. Сосын барлық процесстердің қозғалыспен байланысты болуын болатын режім қарастырылады. Орнықтылықты зерттеудің ең басты мәселелерінің біріне енжар моделдердің дискреттілігінде болып табылады, яғни олардың цикл қадамдары бірнеше деңгейлерден тұрады және олар әрқайсысы өзінше сипаталады.

Орнықтылыққа зерттеудің қарапайым әдістерінің біріне келесідей көрсетілген жүйеден тұрады.

Жақын арадағы қозғалмайтын нүкте ө нақты бейнеде f(Ɵ) де сызықтандыруға болады:

Мұндағы J- f(ө) дегі нақты бейненің якобианы; ө- қозғалмайтын нүктеден келетін кейбір ауытқулар;

Қозғалмайтын нүкте анықтамасы бойынша F(Ө*)=Ө*, сондықтан Өвекторы келесі қадамда Ө өзгереді. Осыдан қорыта келе, егер якобиан мәні белгілі бір аумаықта болса, қозғалмайтын нүкте әрбір қадамда нөлге ұмтылады және қадамдап жатқан жүріс жүйесі орнықты бола түседі.

f(ө) функциясы мен g(ө) функциялары әртүрлі, олардың сипаттамасы 2.5 параграфта айтылған болатын және олардың өзара байласыны келесідей,

Бірқалыпты жүрістің бастапқы мағынасында анықталғандай тәртіп бойынша әрбір массалық-геометриялық параметрлер жүйесі үшін бірнеше бастапқы өадам параметрлері бар, сонын әсерінен бірқалыпты жүріс кезінде қозғалыс жүйесі симметриялы қозғалады. Бірақ та олардың екеуі ғана табиғи жүріске әкеледі, яғни жүріс кезіндегі орын ауыстырып жатқан аяқ жүзеге асырады. Осылардың біреуі ғана орнықты жүріске алып келеді. Зерттеу кезінде жүйе параметрлері жүріс сипаттамасына бірқалыпты орнықты жүріс арқылы мүмікін болатын өзгерістер арқылы әсер ете алады.

φ үшін – 1°-ден 4.3°

β үшін – 0,1°-ден 2°

µүшін – 0,1°-ден 25°

Зерттеу кезінде анықталғандай моделдеу әдісі бойынша парамертлердің төменгі мәнге ие болған сайын жүріс процессі нашарлай түседі. Егер процесс шегіне жеткен болса, жұмыс жасауын тоқтады.

Жүріс кезіндегі жүйенің ерекшеліктеріне жинақтылық аумағынын көлемі әсер етеді. Қозғалмайтын нүктесі 5-10% ауытқитын болса, орнықтылығын жоғалта бастайды. Мұнда α қадам параметрлері ішінде өте сезімтал ,ал θs және θns қозғалыс жүйесінің параметрлеріне аса қатты әсер етепейді.

Екі аяқты жүйені орнықтылыққа зетреттеуде осы әдіс қолданылды. Якобиан 4x4 көлемінде болды және әрбір бастапқы қадамға қосылды. Якобиан мәні белгілі бір аумақты алып жатыр. Соған негіздей отырып мынадай қорытындыға келуге болады, жүріс бұл асимптотикалық түрде орнықты болып табылады.

2.7. Параметрлер жүйессінің жүріске әсері

Екі аяқпен қозғалу жүйесін сипаттайтын тепе теңдік жүйесі орын ауыстыру деңгейін сипаттайтын және аяқ алмасуындағы(2.22) екі алгебралық мәнімен сипатталатын екі екінші дәрежелі бірсызықты емес дифференциалдық тепе теңдіктен тұрады(2.20).

Әзірге зерттеулер бойынша аналитикалық әдістері жоқ. 2.7-2.10 параграфтарда осы тепе теңдіктерге талдау жасалған. Ары қарай жүріс сипатамасына жүйе парамертлерінің әсер етуі қарастырылады. φ жазықтығының қисаю бұрышының өзгеру әсері, сонымен бірге жүріс сипаттамасына әсер ететін масса µ қатынасы және β ұзындығына қатынасы, Т қадам периоды, α – аяқ арасындағы максималды бұрыштың жартысы. Үлкен мағыналы мәндер үшін аталған үш параметрдің екі еселенуі симметриялық жүрістен хаотикалық жүріске әкеледі. Бұл ұғымды арнай жеке бөлімде қарастыруды қажет етеді және келесі бөлімде қарастырылады.

2.6. Қозғалыс жүйесін орнықтылыққа зерттеу

Екі аяқты жүйесін орнықтылыққа зерттеу кезінде ең біріншіден ескере кететін жағдай оның статистикалық тұрғыдан орнықты емес емес екенін анықтайды, яғни қозғалыс жоқ болса құлауын айтып отыр. Бұл жағдайда тек қана динамикалық орнықтылық мүмкін. Сосын барлық процесстердің қозғалыспен байланысты болуын болатын режім қарастырылады. Орнықтылықты зерттеудің ең басты мәселелерінің біріне енжар моделдердің дискреттілігінде болып табылады, яғни олардың цикл қадамдары бірнеше деңгейлерден тұрады және олар әрқайсысы өзінше сипаталады.

Орнықтылыққа зерттеудің қарапайым әдістерінің біріне келесідей көрсетілген жүйеден тұрады.

Жақын арадағы қозғалмайтын нүкте ө нақты бейнеде f(Ɵ) де сызықтандыруға болады:

Мұндағы J- f(ө) дегі нақты бейненің якобианы; ө- қозғалмайтын нүктеден келетін кейбір ауытқулар;

Қозғалмайтын нүкте анықтамасы бойынша F(Ө*)=Ө*, сондықтан Өвекторы келесі қадамда Ө өзгереді. Осыдан қорыта келе, егер якобиан мәні белгілі бір аумаықта болса, қозғалмайтын нүкте әрбір қадамда нөлге ұмтылады және қадамдап жатқан жүріс жүйесі орнықты бола түседі.

f(ө) функциясы мен g(ө) функциялары әртүрлі, олардың сипаттамасы 2.5 параграфта айтылған болатын және олардың өзара байласыны келесідей,

Бірқалыпты жүрістің бастапқы мағынасында анықталғандай тәртіп бойынша әрбір массалық-геометриялық параметрлер жүйесі үшін бірнеше бастапқы өадам параметрлері бар, сонын әсерінен бірқалыпты жүріс кезінде қозғалыс жүйесі симметриялы қозғалады. Бірақ та олардың екеуі ғана табиғи жүріске әкеледі, яғни жүріс кезіндегі орын ауыстырып жатқан аяқ жүзеге асырады. Осылардың біреуі ғана орнықты жүріске алып келеді. Зерттеу кезінде жүйе параметрлері жүріс сипаттамасына бірқалыпты орнықты жүріс арқылы мүмікін болатын өзгерістер арқылы әсер ете алады.

φ үшін– 1°-ден 4.3°

β үшін –0,1°-ден 2°

µүшін –0,1°-ден 25°

Зерттеу кезінде анықталғандай моделдеу әдісі бойынша парамертлердің төменгі мәнге ие болған сайын жүріс процессі нашарлай түседі. Егер процесс шегіне жеткен болса, жұмыс жасауын тоқтады.

Жүріс кезіндегі жүйенің ерекшеліктеріне жинақтылық аумағынын көлемі әсер етеді. Қозғалмайтын нүктесі 5-10% ауытқитын болса, орнықтылығын жоғалта бастайды. Мұнда α қадам параметрлері ішінде өте сезімтал ,ал θsжәне θns қозғалыс жүйесінің параметрлеріне аса қатты әсер етепейді.

Екі аяқты жүйені орнықтылыққа зетреттеуде осы әдіс қолданылды. Якобиан 4x4 көлемінде болды және әрбір бастапқы қадамға қосылды. Якобиан мәні белгілі бір аумақты алып жатыр. Соған негіздей отырып мынадай қорытындыға келуге болады, жүріс бұл асимптотикалық түрде орнықты болып табылады.

2.7. Параметрлер жүйессінің жүріске әсері

Екі аяқпен қозғалу жүйесін сипаттайтын тепе теңдік жүйесі орын ауыстыру деңгейін сипаттайтын және аяқ алмасуындағы(2.22) екі алгебралық мәнімен сипатталатын екі екінші дәрежелі бірсызықты емес дифференциалдық тепе теңдіктен тұрады(2.20).

Әзірге зерттеулер бойынша аналитикалық әдістері жоқ. 2.7-2.10 параграфтарда осы тепе теңдіктерге талдау жасалған. Ары қарай жүріс сипатамасына жүйе парамертлерінің әсер етуі қарастырылады. φ жазықтығының қисаю бұрышының өзгеру әсері, сонымен бірге жүріс сипаттамасына әсер ететін масса µ қатынасы және β ұзындығына қатынасы, Т қадам периоды, α –аяқ арасындағы максималды бұрыштың жартысы. Үлкен мағыналы мәндер үшін аталған үш параметрдің екі еселенуі симметриялық жүрістен хаотикалық жүріске әкеледі. Бұл ұғымды арнай жеке бөлімде қарастыруды қажет етеді және келесі бөлімде қарастырылады.

2.8. Жазықтықтағы қисаю бұрышының жүріс параметріне әсер етуі

Жазықтықтағы қисаю бұрышының жүріс параметріне әсер етуін зерттеуде µ=2 және β=1, φ бұрышы 0.25-тен 5°С әрбір қадамда 0.25°С өзгеріп отырады. Жүріс параметрлерінің өзгеруі 2.11 және 2.12 суреттерде көрсетілген. Жүріс сипаттамасы бұнда функциялар ретінде көрсетілген.

2.11 суретте φ жазықтығының қисаю бұрышының аяқ арасындағы максималды бүрыштардың жартысы α. Графиктан көріп тұрғандай жазықтық бұрышы үлкейген сайын α үлкейе түседі. Барлық қалған жүріс сипаттамалары параметрлеріде өсіп отырады.

2.12 суретте µ=1 және β=2, φ=1.5° тең болатын екі аяқпен жүру портреті көрсетілген. Графиканың І-ІІ және ІІІ-ІV бөлімдеріне ерекше назар аударыңыз. Мұнда аяқ ауыстыру кезіндегі жылдамдықтың өзгеру көрсетілген. Бұл құбылыс аса үлкен назар аудааруды қажет етеді, себебі түсетін салмақ мәні теріс болса жүйе орнықтылығына әсер етеді.

Толығымен айтқанда, бұл жүйе жазықтықтағы қисаю бұрышының үлкеюі қадамдарды жиілетеді және улкейтеді.

2.9. Масса ұатынасының әсері

Бұл жағдайда β=1 және φ=1°,2°,3° тең болатын жағдай қарастырылады. Масса қатынасы µ 0,1-ден 1-ге дейін әрбір қадамнан кейін 0,1-ден және1- ден 10-ға дейін.

2.3-суретте α- ның µ-ға тәуелділігі көрсетіледі. Үзік сызықтармен φ=1° болған жағдайда, ал φ=2°пунктирлі сызықпен жағдайда, φ=3°тура сызықпен көрсетілген.

2.4 суретте Т- ның µ-ға тәуелділігі көрсетіледі. Үзік сызықтармен φ=1° болған жағдайда, ал φ=2°пунктирлі сызықпен жағдайда, φ=3°тура сызықпен көрсетілген.

2.5 суретте µ мәнінің әртүрлі мағынадағы сызбысы көрсетілген. Бірінші нөмерлі графикте µ=0.4 тең жағдайы, екінші нөмерлі µ=1 болған жағдайдағы сызба көрсетілген.

Қадам Т периоды және аяқ арасындағы бұрыштың мәні µ өсуіне байланысты.

µ=2 тең болғанда және үш әртүрлі қисаю бұрыштары φ=1°,2°,3° тең болатын жағдай қарастырылады. Ұзындық қатынасы β 0,1-ден 10-ға дейінәр қадам 0,1 тең.

2.10. Ұзындық қатынысының әсері

2.16-суретте α- ның β -ға тәуелділігі көрсетіледі. Үзік сызықтармен φ=1° болған жағдайда, ал φ=2°пунктирлі сызықпен жағдайда, φ=3°тура сызықпен көрсетілген.

2.17- суретте Т- ның µ -ға тәуелділігі көрсетіледі. Үзік сызықтармен φ=1° болған жағдайда, ал φ=2°пунктирлі сызықпен жағдайда, φ=3°тура сызықпен көрсетілген.

2.18-суретте β–ның әртүрлі мағынадағы екі аяқпен жүрудің фазалық сызбасы көрсетілген. Бірінші нөмерлі график β=0.6 тең болған жағдай көрсетілген, ал β =1 болғандағы мәні көрсетілген. Т,α мәндері β–ның мәнің өсуіне байланысты өзегереді.

2.11. Бифурация(бір нәрсенің екі бағытқа бөлінуі немесе екі бағытқа кетуі) және жүріс периодын көшірмелеу

Қадамдап келе жатқан жүйенің айтылған параметрлерінің (φ, β, µ) мәнінің үлкеюі бифурация немесе жүріс периодын көшірмелеу болып табылады. Бірқалыпты жүрістен екіқалыпты жүріске өзгеруі, яғни қадам параметрлері бастапқы мағынасына оралады, ол жүрістің соңында емес, арбір қадамнан кейін. Алдағы уақытта параметрлер мағнасы өскен сайын екіпериодты жүріс төртпериодты жүріске, ал төртпериодты жүріс сегізпериод жүріске айналып отырады солай ары қарай жалғасады. 2.19-2.21- суреттерде көрсетілгендей әрбір көшірмелеу үшін аз өзгерістер жеткілікті.

2.22- 2.23 суреттерде екі және төртпериодты жүрістер сәйкесінше көрсетілген. Әрбір аяқ өзіне тән траектроиясы бар және ол басқа аяқ траектороиясынан ерекшеленеді. Бір аяқтың траекториясы сызбада үзік сызтармен көрсетілген, ал екіншісі штрихты сызықтармен көрсетілген. Барлық көппериодты жүрістерде келесідей заңдылық байқалады: бір аяқ басқа аяққа қарағанда үлкен қадамдар жасап отырады. Көппериодты жүріс симметриялы болып табылмайды. Сонымен бірге, төрт немесе одан да көп периодты тракетрориялы аяқтар бір біріне жақын үлкен қадамдар жасайды. (2.23 суретте көрсетілген).

2.19 сурет. Буфиркация жазықтық қисығы бұрышының жоғарылауы

2.7-2.10 параграфта берілген, модельдеуден басқа көппериодты жүрісті зерттей келе барлық әдісті қолдануға болады.

Өте жоғары дәлдікпен байланысқан қиындықтар қатары туады.(кейбір қадамдар бір-бірімен баяу ажыратылады). Бұл жаңа математикалық пакеттің қолданудағы уақыты маңфызды шығынға алып келеді.

2.20-сурет. Β мәнінің бифуркациясының жоғарылауы

2.21-сурет. µ мәнінің бифуркациясының жоғарылауы

2.22-сурет. Фазалы екіпериодты жүрістің суреті.

2.23-сурет. Фазалы төртпериодты жүрістің суреті.

Ережені сияқты, бақылау 8-16 мерзімді қозғалыстан кейін параметрде үлкеюде мерзімділік жаттығу мүмкін емес, және жүріс осылай называесую хаосты екі бірдей қадамға өте күрделі табу айналдырып жатыр. Қараңғылық кем болмайды кейбір заңдылыққа ; осылай, артында қысқа ұзын адыммен міндетті түрде шығып жатыр.

2.12. Аяқтың иілгіштігі мен массаның таралуын негізге ала отырып, жүру процесін модельдеу

Масса, қарастырып отырған модельдегідей, әр нүктеде емес аяқтың барлық ұзындығы бойынша таралған.

Модель неғұрлым шындыққа сай болған сайын, ол соғұрлым матема-тикалық қиын болады. Себебі, мысалы, призматикалық шарнирлы модель аяқтың тіреу жазықтығымен жанасуын болдырмайды. Бірақ, бұл жағдайда динамикалық теңдеулер жүйесі анағұрлым қиындайды. Тіреуіш аяқ жанасқан нүктеде тіреу жазықтығы орналасқан деген шешім қабылдауымызға бола-ды.Өткен тақырыпта айтылғандай, лагранждар формализмін қолданып, тек сандық түрде шешілетін, екінші қатарлы сызықты емес дифференцилдық теңдеулер жүйесін алуымызға болады.

Кинетикалық моменттің сақталу заңына сүйеніп, аяқтардың алмасу процесін суреттейтінекі алгебралық теңдеулер жүйесін аламыз. Цилиндрдың гидравликалық күші, көлемі цилиндрдың бекітілу шартына байланысты тізе тәріздес буын моментімен байланысты.

Қадамына мерзіміне м олардың ықпалынан массалардан тұрғыдан, қатынастан көлбеуден бұрыштан параметрлерден тәуелділікте алған теңдеулердің шешімдердің зерттеуі көрсетіп жатыр, не мәніне үлкеюде симметриялық жүріс көппериодты айналдырып жатыр, ал содан соң хаосты. Жүріс жүйеде едәуір үлкен жаппай-геометриялық параметрлерде орнықтылық жоғалтып жатыр. Массада жағдайда үздіксіз бөлулерде бифуркацияда µ параметрде анағұрлым кіші мәндерде көрініп қалып жатыр.

Аяқтарда қозғалыста пішіндеуде буындардың тығыздықтары есепке алуы маңызды болып табылады. Жалпы алғанда жағдайға сызықты емес дифференциалды теңдеулердің күрделі жүйе пайда болады. Байланыста ойын тасыларда және буындарда бұзылулар жинақтау процесстер сипаттама үшін қолданған сызықты жуықтаумен шектелу бұл дәл келеді.

Алған теңдеулердің коэффициенттері бұзылулардың жинақтаулары есепке алуы алып келіп жатыр - айнымалы функциялар және жағдайда периодты тәуелділіктер периодты жүрісті суреттеп жатыр, процесы циклдік шаршауда ағатын. Ұқсас үлгі қолданыла алады, мысалы, шеміршек кездемеде сүйек ұлпасының селдіде, азып-тозуда сипаттамада т.б.

Бұзылулардың жинақтауы тәжірибелі бақылауларға негізде анықталған кейбір кинетикалық теңдеулермен суреттеледі. Дәрежеден тәуелділікте үлгілер тиімді серпімді параметрлері өзгеріп жатыр, не жүріске мерзімділікке бұзушылыққа алып келеді.

2.13. Екі аяқта протезбен адамдың жүрістері пішіндеуі

Протездер жобалау үшін биоинженерияда қолдануға болатын тұрғыда қозғалыста адамның үлгісі қарап шығамыз.

2.24 сурет. Адамның жетібуынды схемасының үлгісі.

1-басы-дене. 2-екі-үшбуынды аяғы- (бөксе,сирақ,стоп)

Массалардың орталықтың орын ауыстыруы х_с(t), у_с (t) теңдеулермен суреттеледі.

mẍ_с(t)=F_x

my_с(t)=F_y

F= (F_x,F_y)

Аяқтардың және корпустың жағдайы қорытған лагранжевы координаталардың артына қабылдайтын бұрыштық айнымалы анықталып жатыр. Үлгіден тәуелділікте добаваит 2-6 координаталардың қолдың динамикалары есепке алуы.

Кинетикалық энергия үшін өрнектер маңызды жазып алу керек Лагранж формализм теңдеулер алу үшін Т(q_i,q_i.t) . Ол координаталарға және қорытған координаталарға кениговой жүйеде жазып алған буындардан кинетикалық энергиялардан сомалардан тұрады.

Мейлі үлгілер қозғалысы буындарға қосымша тіркелген сәттердің есептің y=0артына іске асып жатыр, ал бетпен байланысу тіректер реакциялары R вектормен суреттеліп жатыр.

Екінші тектерге Лагранжға теңдеулерге формада жазып алған жүйелер рассаматриваемой үлгілері қозғалыстар теңдеулері жалпы алғанда түрге, түр алынады.

(2.37)

Мұнда, A B C D E-матрица;

Кибернетикалық жүйеді сияқты үлгі қарап, қозғалыстар тап қалған тәртіп қамтамасыз ететін жүйеде басқаруды сияқты вектор бағалайды.

Былай делік, не бір аяқ өзі протез ұсынып жатыр, және ары қарай 1-индекске сау аяққа жату болады, ал 1 индекс протез жасаған. Комфортты максималға жақын жүрген адам жүрісті қамтамасыз ету үшін, протезбен басқару осылай іске асуға тиісті. Жамбас буындарда сәттер бағдарлаушылар- u₁,u₂ деп белгілейміз, балтыр- p₁,p₂. Бойынша тіректер көлденең реакция белгілейміз, тік- .

Маңызды жасау протезде басқаруда заңдарда құрастыруда ырғақты жүрісте оның биомеханикалық функционалдық қамтамасыз ететін басқарулар жүйеді және тәртіпте ауысымда бейімделуді.

Критерийдін ықтимал варианты(19)

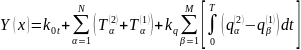
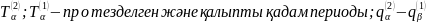- протез жасаған және нормалы қадам бойынша қорытылған координаталар. N-қадам саны; М- бақыланған координаттар саны; Т₀-бақылау уақыты; k_t, k_q –келтірілген коэффициенттер.

Уақыт және координаталар бойынша келіспеулер шаршының минимум нормалы талап ететін белгі 3 және протез жасаған қадамды, кері байланыста басқаруларға жүйеде бар болу себепші болып жатыр. Басқарудан адапттивті жүйемен протезде жасауда пайда болып жатыр сонымен бірге массалар мәселе : протезді, қозғаушыны, еріксіз келтірулерді, процессорларды. Энергия көп үнемді жұмсау үшін энергиялар рекуператорлармен жарақтанған протездер өндеп жатыр. Екі аяқта жүрісте әдетте масса тасымалданатын аяқтар кинетикалық энергияы дене, есеп диссипирует артында қаққы және үйкеліс,, ол біржолата жоғалып жатыр. Қағидада бұл энергия қысылған потенциалдық энергияға ішінара өте алады газа немесе серіппені, ал жолдан жамылғыдан итеруде содан соңы қолдану керек.

Протездерде жобалауда және жасауда қолдануға болатын энергиялар рекуператорлардың үлгілері қарап шығамыз(19).

Өзі гидравликалық серіппені рекуперационды пневмоцилиндр ұсынып жатыр, қаттылық піскекте және цилиндр болған екі қайта жіберетін клапандарымен қайсы реттелді. Клапандардың қималары өзгерістері, протездің пневмоцилиндрді тізе буынына берілетін күш реттейміз. Цилиндр өсі бойынша, цилиндрмен қатты сабақтас координаталарда жүйеде өс бағыттаймыз.

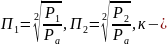адибатты газдың көрсеткіші; Р₁, Р₂- пневмоцилиндрдің сызықты қысымы, Р_а-ауа қысымы, 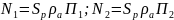(S_p-поршень аумағы, .

Пневмоцилиндра динамикаларға суреттейтін теңдеуді, ал екі камералы тәртіпті, түр алып жатыр:

m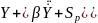 - 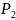)=F

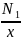+ (lnP₁) Y=Q₃+Q₄, (lnР_і)=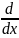 (lnP_i), і=1, 2, (2.39)

N_{2 -} L_p-Y)=Q₃

Мұндағы, L_p-цилиндр ұзындығы; Y-поршень жүрісі; 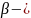байлағыш үйкелістер коэффициенті; F- поршень штогіне жұмыс істейтін күш; Q₃; Q₄-клапан арқылы өтетін шығын.

Дифференциалды теңдеулердің бұл күрделі сызықты емес жүйе Y, P₁, P₂ туралы. Шығыстар формула бойынша СенВенана және турбулент дроссел арқылы жаппай шығыс Ванцеля үшін Q₃, Q₄ есептеп жатыр .

Қолданған мүмкін болу сирақ қозғалыс басқару үшін кірістірілген серіппемен және қайта жіберетін клапанмен су цилиндр.

Координаталарға жүйеде цилиндр динамикалары үлгісі қатты (өстен цилиндрме( цилиндр өс бойынша Y₁ бағыттаған), түр алып жатыр:

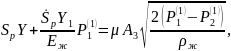
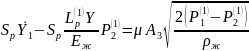
C-пружинаның қатаңдығы;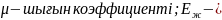 сұйықтаркөлемдітығыздықтарымодулі; 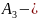көлденең қималар дросселдер ауданы.

Дифференциалды теңдеулердің жүйесі (2.40) , сонымен бірге сызықты емес.

Сонымен, протездің моделінің құрамына басқарылуы тиіс пневмогид-роцилиндр (ПЦ, ГЦ) және серіппелі механизмдер кіреді. Қарастырылып отырған серіппелі механизм типінде өзгеретін көлем болып, арнайы арбаша-ны жылжыту арқылы өзгеретін, серіппенің қаттылығы саналады. Осының ар-қасында протезге берілетін тізе тәріздес буынның моментін басқаруға бола-ды. Атқарушы болып көрсетілетін момент Мор интегралы арқылы есептеле-ді [19].

ДТХ

ПБ

ЭМСС

Протездің берілісінің мүмкін сандық жүйесімен басқарылатын схема-сын қарастырайық [19].

ПМ

ПДУ

2.25-сурет. Протезді басқару схемасы

Басқару жүйесі процессорлық блок (ПБ) және электромеханикалық ба-қылау жүйесінен (ЭМСС) тұрады (2.25-сурет).

Процессордың есте сақтау құрылғысында (ЗУ), жүрісті үйрету кезінде пайда болатын бекітілген жүріс екпіні баптаулары орналасқан.Жүріс екпіні-нің датчигі (ДТХ) процессорлық блокқа жібереді. Ол сигнал серіппе меха-низмін (ПМ) басқаруға жіберілген сигналды қабылдап, реттеп, жіберетін сиг-нал. Арбашаның орналасуы, функциялануы дифференциялық теңдеулер жү-йесімен суреттелетін, электромеханикалық бақылау жүйесімен бекітіледі [19]:

τ₁ẋ₁=F[(u-K_rэ)K_y]K_{db ,}

τ₂ẋ₂ - x₂=x₁ , (2.41)

i_p ẋ₃=x₂ ,

мұндағы τ_1, τ₂-жүйені синтездеу кезінде анықталатын уақыт тұрақтылары;

K_rэ , K_db , K_y-rэ, күшейткіш және қозғалтқыштың тұрақтылары;

и- якорь кернеуі; i_p- редуктордың беріліс саны; х₁, х₂, х₃- күйдің ауыспалылары; Ғ[x]- қаныққан кернеуді эмулирлейтін функционал.

Осы себепті, аяқ қасиеттерін қабылдай алатын протез үлгіленіп, жасалуы мүмкін.