
- •1.Қатты дене
- •2. Сұйық дене
- •3.Газ тәрізді дене
- •1.2. Механикалық кернеуден болатын деформация
- •1.3. Деформациялану жылдамдығы, ротор.
- •1.4. Механиканың бірыңғай ортасы үшін жалпы заңдылықтар мен теңдеулер
- •1.5 Тұтас орта термодинамикасының заңдары.
- •1.6 Гипстің тепе- теңдігі және диссипоция теңсіздігі
- •1.7 Онзагер принципі
- •1.8. Еркін (бос) энергия, энтальпия, Гиббстің термодинамикалық потенциалы
- •1.9. Тұтас ортаның кейбір математикалық моделі (үлгісі)
- •1.11. Ашық жүйелердің термодинамикасы
- •2.1. Адамның қарқынды қозғалмалы жүйесінің құрылымы
- •2. 5 Сурет. Бас сүйек жазықтығының сагиттальды иінтірегі [5]
- •2. 6 Сурет. Табан мен оған әсер ететін күштер бейнеленген.
- •2. 6 Сурет. Аяқтың ұшымен тұру [5]
- •2. 7 Сурет. Білек пен оған әсер ететін күштер бейнеленген.
- •2. 7 Сурет. Білек сүйектері, тіректі ұстап тұруы
- •2.2. Жердің ауырлық даласында екі аяқпен жүру кезінде дене массасының қозғалыс орталығы
- •2.8 Сурет. Масса орталығының бір қадамға өзгергендегі жүрген жолы
- •2. 3. Дөңгелек жүріс кезінде аяқтардың динамикасын теңестіру, қозғалыстың кезеңдері бойынша талдау
- •2.9 Сурет. Екі аяқты жүйенің моделі
- •2.4 Тұрақты әрекетсіз циркуль жүрісіне сипаттама
- •2.5 Бір периодтық жүріс кезіндегі төзімділік параметірлерін анықтау
- •2.14. Негізгі жалпы теория негізіндегі жүйенің биомеханикалық қозғалысы тепе-теңдікті қалыптастыру
- •2.15. Қозғалыс теңдеуін құратын көпзвеналық динамикалық жүйенің Лагранж формализмін қолдана отырып, деформацияланған элементтер құрылымы
- •2.16. Биомеханикалық бұрандама қозғалыс жүйесі бар, деформацияланған элемент құрылысының теңдеуі мен моделі
- •2.27 Сурет. Жазық қозғалысының бұрандама механикалық жүйесі мен бір тірек фазадағы өзгертілетін геометриялық буын моделі
- •2.17. Механикалық жүйелер элементтердің серпімді модулін анықтау
МАЗМҰНЫ
КІРІСПЕ .................................................................................................................. 6
Механикадағы модельдеу ..................................................................................... 8
Қатты дене .................................................................................................... 8
Сұйық дене ................................................................................................... 9
Газ тәрізді дене ............................................................................................ 9
Тұтас және дискретті орталар механикасы ............................................. 10
1 ТАРАУ. ТҰТАС ОРТАЛАР МЕХАНИКАСЫНЫҢ НЕГІЗГІ ТҮСІНІКТЕРІ МЕН ЗАҢДАРЫ .................................................................................................. 12
Лагранж және эйлер координаттары ............................................. 12
Деформация тензорлары ................................................................. 15
Деформация жылдамдығы, ротор .................................................. 17
Тұтас орта механикасының жалпы заңдары мен теңдеулері ...... 18
Тұтас орта термодинамикасының заңдары ................................... 22
Диссипация теңсіздігі және Гиббс тепе-теңдігі ........................... 26
Онзагер қағидасы ............................................................................ 28
Бос энергия, энтальпия, Гиббстің термодинамикалық потенциалы ............................................................................................. 29
Тұтас орталардың кейбір математикалық модельдері ................. 29
Ақпарат теориясы және термодинамиканың екінші заңы. Құрылымдық тәртіп және тәртіпсіздік .............................................. 31
Ашық жүйелер термодинамикасы ................................................. 34
Биологиялық жүйелердегі зат алмасу үрдісін модельдеу ............ 38
Бақылау сұрақтары .................................................................................... 46
2 ТАРАУ. ЕКІ АЯҚПЕН ЖҮРІС ҮШІН ТІРЕУІШ-ҚИМЫЛ ЖҮЙЕСІНІҢ МЕХАНИКАСЫ (А.Ф.Смалюкпен бірлесіп) ................................................... 47
Адамның тіреуіш-қимыл жүйесінің құрылымы ........................... 47
Жердің ауырлық өрісінде екі аяқпен жүріс кезінде дене салмағының орталығының қозғалысы ............................................. 53
Шеңберлі жүріс кезінде аяқ динамикасының теңдеулері, қозғалыстың кезеңдері бойынша талдау ............................................ 56
Орнықты пассивті шеңберлі жүріс үрдісінің сипаттамасы ......... 61
Орнықты бір периодты жүрістің параметрлерін анықтау ........... 62
Жүйе қозғалысын орнықтылыққа зерттеу .................................... 65
Жүйе параметрлерінің оның жүрісіне әсері ................................. 66
Көлбеу бұрышының жүйе жүрісінің параметрлеріне әсері ........ 67
Салмақ қатысуының әсері .............................................................. 68
Ұзындық қатысуының әсері ........................................................... 70
Бифуркациялар және жүріс периодының қайталануы ................. 71
Аяқ серпінділігі және салмақ бөлінуі ескерілген жүріс үрдісін модельдеу .............................................................................................. 74
Екі аяғына протез салынған адамның жүрісін модельдеу .......... 75
Жалпы теориялар негізінде көп буынды биомеханикалық жүйе қозғалысының теңдеулерін құрастыру ............................................... 79
Лагранж формализмін қолдану арқылы деформацияланатын құрылым элементтері бар туынды көп буынды динамикалық жүйе қозғалысының теңдеулерін құрастыру .............................................. 85
Деформацияланатын құрылым элементтері бар өзекшелі биомеханикалық жүйе қозғалысының моделі және теңдеулері ...... 87
Механикалық жүйе элементтерінің серпінді модульдерін анықтау .................................................................................................. 101
Бақылау сұрақтары .................................................................................. 103
3 ТАРАУ. БҰЛШЫҚЕТ ТІНДЕРІНІҢ МЕХАНИКАСЫ ................................ 104
Бұлшықет тіндерінің феноменологиялық модельдері ............... 104
Хилл моделі. Жеке жиырылудың қуаты ...................................... 109
Бұлшықеттің жұмыс істеуін құрылымдық жағынан модельдеу .. 111
Бұлшықеттің жұмыс істеуін құрылымды-феноменологиялық жағынан модельдеу ............................................................................ 117
Адамның тіреуіш-қимыл жүйесінің құрылымды-феноменологиялық моделі................................................................. 121
Бұлшықеттің жұмыс істеуі кезінде дірілдің және температураның рөлі ....................................................................................................... 123
Биомеханиканың модельдерінің спортта қолданылуы .............. 133
Бақылау сұрақтары .................................................................................. 135
4 ТАРАУ. ЖҮРЕК ҚАНТАМЫР ЖҮЙЕСІНІҢ МЕХАНИКАСЫ ................. 136
Қан айналым жүйесінің функционалдық сұлбасы ..................... 136
Жүрек динамикасын модельдеу ................................................... 141
Бұлшықетті қанмен қамтамасыз ету сұлбасы ............................. 158
Қанның және тамырлардың механикалық қасиеті. Құрылымы бар орталардың тиімді модельдері туралы түсінік ................................ 161
Кейбір модельдер және гемодинамика заңдары ......................... 166
Серпінді тамырлардағы қан айналымның кинетикасы. Пульстік толқын. Франк моделі ....................................................................... 170
Физико-механикалық қасиеті ескерілген қанның артерияда ағуы және қысымы ...................................................................................... 177
Тамыр геометриясының ағынға әсері ......................................... 184
Қанның микроциркуляциясы ....................................................... 191
Соғып тұрған (пульсирующий) қан ағысының микроконтинуалды моделі .................................................................................................. 193
Бақылау сұрақтары .................................................................................. 194
5 ТАРАУ. КАПИЛЛЯР ЖӘНЕ ЖЕРГІЛІКТІ ТАРЫЛҒАН ТАМЫРЛАРДАҒЫ ГЕМОДИНАМИКА .......................................................................................... 196
Қанның капиллярда сүзілуі және реабсорбциясы ...................... 196
Тамырлардың жергілікті тарылуы кезіндегі қан ағысының ерекшеліктері. Резистивті модель ..................................................... 204
Бақылау сұрақтары ................................................................................. 212
6 ТАРАУ. ТАМЫР ІШІ ХИРУРГИЯСЫ ҮШІН СТЕНТТЕРДІ ҚОЛДАНУ .. 213
Стенттер инженериясы (В.Т.Минченмен бірлесіп) .................... 215
Түтікше құрылымды артерия стенттерінің орнықтылығы және радиалды қаттылығы (В.Т.Минченмен бірлесіп) ............................ 223
Тиімді серіппенің жақындауы кезінде стент орнықтылығының теңдеуі ................................................................................................. 236
Бақылау сұрақтары .................................................................................. 239
7 ТАРАУ. ЕСТУ БИОМЕХАНИКАСЫ ............................................................ 240
Есту жүйесінің жалпы анатомиясы және оның жұмыс істеуі ... 240
Қалыпты жағдайдағы ортаңғы құлақтың қарапайым динамикалық моделі .................................................................................................. 244
Дабыл жарғағындағы бастапқы кернеуді бағалау туралы міндеттердің қойылуы ....................................................................... 250
Бақылау сұрақтары .................................................................................. 255
8 ТАРАУ. ҚАЙТА ҚҰРЫЛҒАН ОРТАҢҒЫ ҚҰЛАҚТЫ МОДЕЛЬДЕУ ...... 256
Қайта құру операцияларының классификациясы ...................... 256
Қайта құрылған ортаңғы құлақтың кернеулі-деформацияланған жағдайы ............................................................................................... 258
Қайта құрылған ортаңғы құлақтың еркін тербелісін модельдеу ............................................................................................ 268
Қайта құрылған ТМ-нің өзіндік тербеліс пішініне диссипативті күштердің және иілгіш қаттылықтың әсері ..................................... 273
Тимпанопластика және стапедопластика жағдайындағы протез қозғалысының айналмалы пішіні ..................................................... 275
Бақылау сұрақтары .................................................................................. 280
ӘДЕБИЕТТЕР .................................................................................................... 281
Кіріспе
Инженерлік биомеханика табиғат жобалап және жаратқан құрылым механикасының бөлімі ретінде көптеген ғылыми-техника қызметкерлеріне қажет.
Биоқұрылымдарды модельдеу үшін математикалық база ретінде тұтас және дискретті орталар теориялық механикасы, лагранж және гамильтон формализмдері, сақталу заңдары жиі қолданылады. Организмдегі жылулық, химиялық, физткалық процесстер биологиялық құрылым үшін маңызды. Биомеханика модельдерін жасау кезінде термодинамика заңдарын және соған сәйкес әдістерді қолдану қажет. Классикалық механика әдістерімен жасалынған модельдер диссипация ескерілмеген жағдайда уақыт бойынша қайтымды. Тепе-теңдік термодинамика әдістерімен жасалынған модельдерде нақты нысандарға сәйкес келмейді.
Биологиялық жүйелер ашық болып табылады (қоршаған ортамен энергия, зат, ақпарат алмасу орны бар), олар термодинамикалық тепе-теңдік жағдайынан алшақ. Осыған байланысты жалпы жағдайда тепе-теңсіздік термодинамикасының заңдары мен әдістерін қолдану керек. Тепе-теңсіздік жағдайынан тепе-теңдік жағдайына өту процесі энтропияның көбеюі және диссипация арқылы жүреді. Сондықтан осындай процесстер уақыт бойынша қайтымсыз.
Классикалық және статикалық механиканың жалпы принциптерін салыстырсақ, олардың тек айырмашылықтарын ғана емес, сонымен қатар олар бір-біріне қарама-қарсы екенін көруге болады. Механика (классикалық және кванттық) аз әсер кезінде жасалуы мүмкін. Консервативтік жүйелер үшін лагранж және гамильтон формализмдерінің базасы негізінде уақыт бойынша қайтымды (диссипациясыз) математикалық модельдер жасалады. Биологиялық құрылымдар жүйеге келіп түсетін энергияны жасайтын еркіндік деңгейлеріне ие.
Нақты жүйелерде диссипация бар, алайда оларда эволюция процесі кезінде оның өсуіне кедергі келтіретін еркіндік пайда болды. Еркіндік деңгейлерінің иерархиясы нәтижесінде уақыттың әр сәтінде жүйеде еркіндіктің басым деңгейлері бар, оларда жүйеге келіп түсетін энергия шоғырланады. Соның арқасында термодинамикалық тепе-теңдік жағдайында жүйенің релаксациясы термодинамика заңдарының болжамына қарағанда анағұрлым баяу болады. Бұл еркіндіктің басым деңгейлерімен байланыспаған немесе әлсіз байланысқан еркіндік деңгейлерінің термодинамикалық тепе-теңдікке жақын орналасуынан болады. Жалпы биологиялық құрылымдарды классикалық механика әдістерімен сипаттауға болмайды. Алайда кейбір еркіндік деңгейлерінің жүріс тәртібі механикалыққа жақын болуы мүмкін.
Биологиялық жүйелердегі процесстердің ерекшелігіне олардың мерзімділігі жатады. Бұл жүйеде энергияның рекуперация процесінің өтіп жатқанын білдіреді. Осы маңызды болатын еркіндік деңгейлерін механикалық модель негізінде сипаттауға болады. Себебі мерзімділік толық энергия (кинетикалық және потенциалдық) үшін сақталу заңының орындалғанын айқындайды. Энергия рекуперациясы энергия диссипациясын алып тастау немесе елеулі азайтуға мүмкіндік береді.
Биологиялық құрылымдардың ерекшелігіне олардың қоршаған ортамен ақпарат алмасуы жатады және сол ақпаратты жүйеде өтетін процесстерді басқару үшін қолданады. Жүйенің ортамен ақпарат алмасуының әсерінен биологиялық құрылымдарда энтропия (тәртіпсіздік) өлі табиғат құрылымына қарағанда қиын түрде өтуде.
Осылайша биомеханика ғылым ретінде ақпарат теориясы, термодинамика және механика заңдарына негізделуі қажет. Әр жағдайда белгілі еркіндік деңгейлеріне механика немесе термодинамика заңдарын қолдануға болады. Уақыт келе биологиялық жүйелер үшін жалпы принциптер жасалуы мүмкін. Соның негізінде модельдерді жасау формальді процесске айналуы мумкін.
Осылайша биомеханикада модельдерді жасаудың негізі ретінде ақпарат теориясы, термодинамика және механиканың басты заңдарын қабылдауға болады. Біріші тарауда ақпарат теориясы, термодинамика және механиканың негізгі анықтамалары мен принциптері тұжырымдалған.
С




ФИЗИКА
Механика
Биофизика
Биомеханика
БИОЛОГИЯ
Биохимия
Химия




 уретте
биомеханиканың тұжырымдамалары мен
негізгі дисциплиналарының арасындағы
байланысы көрсетілген.
уретте
биомеханиканың тұжырымдамалары мен
негізгі дисциплиналарының арасындағы
байланысы көрсетілген.
Биомеханиканың тұжырымдамалары мен негізгі ғылыми-табиғи дисциплиналарының арасындағы байланысы
Механикадағы модельдеу
Механика денелердің өозғалысын және өзара қатынасын зерттейді. Дене ұғымы түсінігінде кеңістік көлемі дегенді білдіреді, яғни денелерді құрайтын материалдар бөлігі. Механика қатты, сұйық және газ тәрізді денелерді зерттейді.
1.Қатты дене
Қатты дене оның формасының және көлемінің өзгеруіне кедергі болады. Абсолютті қатты дене өзіне түскен қандай күш болса да,өз формасын да, көлемінде өзгертпейді, яғни бөліктер арасындағы ара қашықтық өзгермейді. Абсолютті қатты дененің статистика, кинематика, динамика курстары классикалық теория механикасында зерттеледі.
Деформацияланатын қатты дене басқа күштер асерінен өз формасын және көлемін өзгерте алады, яғни денені құрайтын бөліктері арасындағы арақашықтықтың өзгеруі арқасында. Деформацияланатын қатты дененің статистика, кинематика, динамика курстары деформацияланатын қатты дененің теориясы механикасында зерттеледі, олар келесідей бөлімдерден құралған: иілгіштік теориясы, тұтқыриілгіштік теориясы, серпімділік теориясы, жойылу теориясы.
Иілгіштік теориясы демормацияланған қатты денелердің қалыпына келу кезеңі процесін зерттейді, яғни денеге түскен салмақ жоқ болғанда, бастапқы қалпына келеді, сол деформацияланған қатты денелердің қайта қалпына келуін иіглгіштік процесін зерттейді.
Серпімділік теориясы демормацияланған қатты денелерге денеге түскен салмақ жоқ болған жағдайда да бастапқы қалыпына келмейтін процесін зерттейді, яғни соңғы қалыпта қалады өзгерген күйінде, сол деформацияланған қатты денелердің қайта қалпына келмеуін серпімділікпроцесін зерттейді.
Жойылу теориясы жарықтардың пайда болуын және таралуын зерттейтін процесс, яғни ол дененің бөліктерге бөлінуіне алып келеді.
Суретте
мүмкін болатын диаграмма қөрсетілген,
мұнда айтылған кезеңдер көрсетілген
 күш
түсіру және қатты дене үшін деформация
е;
1 – иілгіштік, 2 – серпімділік, 3 – жойылу.
күш
түсіру және қатты дене үшін деформация
е;
1 – иілгіштік, 2 – серпімділік, 3 – жойылу.
2. Сұйық дене
Сұйық дене өзі тұрған форманың көлімін қабылдайды, яғни көлемін өзгертеді. Бұл дегеніміз бөліктердің бір сұйық қабатынан басқа қабатқа орын ауыстыру кезінде болады.
Сұйықтардың әртүрлі бірнеше моделдері өңделген: мінсіз (ішкі үйкеліссіз), тұтқыр (ньютондық, үйкеліс күші қозғалыс жылдамдығына пропорционалды), көпафазалылық және т.б.
Қатты дененің сұйық денеден негізгі айырмашылығы денені құрайтын cұйықтық қабатындағы ішкі үйкелістің болмауы, сайып келгенде ол деформация жылдамдығына негізделген. Қатты дене де мысалы, серпімділік деңгейінде тыныштық күйінде үйкеліс күші орын алуы мүмкін, себебі онда жылдамдығына емес, деформация қозғалысына байланысты негізделген.
Үйкеліс күші мен қозғалыс жылдамдығы арасындағы байланысты реология жалпы заңдылықтары айналысады.
3.Газ тәрізді дене
Газдар мен сұйықтар жалпы ортақ ерекшеліктерге ие: үзіліссіз болуында және қозғалмалы болуында. Сүйықтардың қарағанда газ молекула арақашықтығы алшағырақ, сондықтан олар қысылу ерекшелігіне ие (қысым түскенде көлемнің өзгеруі). Сұйықтар газға қарағанда практика жүзінде қысым түскен жағдай да өз көлемін өзгертпейді.
Сұйықтарда молекулаларының арақашықғының алшақ болуы молекулалық үйкеліс күшіне қатты әсерін тигізеді, ол сыртқы жағына интенсивті әсер ететін сұйықтарды басқа сқйықтардан немесе газдардан бөледі. Осындай күш түскен кезде сұйықтық қатты қысылуына әкеледі. Шектеріне капиллярлық ерекшеліктері бар, мысалы, сұйық денелерде газдарды көпіршіктер арқылы болады.
Гaзда молекулалар хаотикалық түрде қозғалып отырады, яғни макроскопиялық температуда пайда болады. Сұйықтар да жылуық қозғалысында молекула қозғалысы хаотикалық түрде болады. Классикалық механикада сұйықтар мен газдарды сұйықтар деп атайды, айырмашылығын былай түсіндіреді газ болғанда сығылатын және сұйық болғанда сығылмайтын деп айырады. Кей кезде механика сығылмайтын сұйықты гидромеханика деп , ал сығылатын сұйықты аэромеханика деп атайды.
Сұйықтардың қарапайым моделі – мінсіз сұйық, яғни үшкі үйкелістің болмауы және орын ауыстырудың жоқ болуы. Осы модель арқылы дененің каналдар ағып кетуі анықталады.
4. Бірыңғай және дискретті ортаның механикасы
Аталған дене моделдеріне ортақ ерекшеліктер бар, бастысы олар үшін бірыңғайлық, сондықтан барлық денелер үщін жалпы ортақ ерекшеліктерін механиканың бірыңғай ортасы механикасы зерттейді.
Бірыңғай ортаның механикасы келесәдей бөлімдерге бөлінеді: кинематика, статитика, динамика. Кинематикада орын ауыстыру, деформация және олардың жылдамдығы қарастырылады. Статитика бөлімінде күш түсіру, тепе-теңдік теңдігі және кинематикалық күш арқыл байланысатын қатынасытары ұғымдары түсіндіріледі. Диманика бөлімінде тепе-теңдік теңдігі қосымша мүшелермен, яғни бірыңғай ортаны тудыратын материаилдық нүктелердің инерциясын есепке ала отырып, толықтырып отырады. Матиматекалық моделдеу кезінде, бірыңғай орта механикасы теңдігімен басқаратын шектік жіне бастапқы мәндерін жасап алу керек.
Бірыңғай орта механикасысында температура ең басты рөлді ойнайды. Бұл жерде ең бастысы айта кететін жайт, температуны төмендеткен жағдайда сұйық денеге немесе қатты денеге айналдыра алу мүмкіндігі бар. Және керісінше болуы да мүмкін, яғни қатты дене болып температураны көтерген жағдайда, сұйық айналады. Одан газ күіне айналады. Бірыңғай ортаның моделі осы жағдайды кейбір механиканың тапсырмаларын орындау кезінде қолданады. Бірақ та көптеген мақсат қойылған тапсырмалард орындауын кезінде дене материалдық нүкте санының соңғы шегіне сияқты қарастырлады. Мысалы, қатты денені аппроксимилеуге болады, яғни массасына негізделген нүктелер арқылы. Аппроусимилеу кезінде абсолютты қатты дене үшін материалдық нүкте жүйесінде нүктелер арақашықтығы өзгермейді, ал деформацияланатын дене үшін арақашықтық өзгереді.
Материалдық нүкте – бұл мехнаканың негізіг обьектісі , ол арқылы басқа моделдер құралады. Материалдық нүкте матиматека тәрізді , көлімі де жоқ, ондай болған жағдайда формасы да жоқ. Бірақ та, матиматекалық нүктеден айырмашылығы массасының болуында, бұл дегеніміз біріншіден, иннерттілігін білдіреді және оның ең басты ерекшелігі болып келеді.
Механиканың келесі қарастыратын обьектісі материалдық нүкте жүйесі болып келеді. Олардың тәртібі бір нүктеге қарағанда қиындау.
Көптеген материалдық нүктелердің белгілі бір көлемде болуын материалдық континуум немесе бірыңғай орта деп атайды.
Бірыңғай ортадағы негізгі түсініктер мен заңдылықтар
Лагранждық және эйерлік координаталар
Бірыңғай
ортаның қозғалысын анықтау дегеніміз
–бұл дегеніміз нүктелердің қозғалыс
заңдылығын табу дегенді білдіреді.
Жүйеде таңдалған жеке нүктелерге олардың
бастапқы мағынасын берге болады. Егер
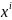 (і
= 1,2,3) і-ші координата нүктесінің t
уақыиындағы
(і
= 1,2,3) і-ші координата нүктесінің t
уақыиындағы
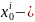 бастапқы
уақыт
бастапқы
уақыт
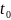 ,
онда континуума өозғалысы заңын келесідей
жазуға болады.
,
онда континуума өозғалысы заңын келесідей
жазуға болады.
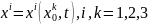 (1.1)
(1.1)
Егер
(1.1) формуласында
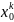 – бекітілген, ал t – айнымалы, белгілі
бір бекілген нүктенің қозғалысы заңын
аламыз. Егер
=
– бекітілген, ал t – айнымалы, белгілі
бір бекілген нүктенің қозғалысы заңын
аламыз. Егер
=
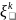 болса және
айнымалы
деп есептеп, ал t – бекітілген болса,
континумма нүктелері t уақыт бойынша
орындалады. Егер t және
-айнымалы
болса, онда бұл теңдеу бірыңғай орта
қозғалысы заңымен анықталады.
болса және
айнымалы
деп есептеп, ал t – бекітілген болса,
континумма нүктелері t уақыт бойынша
орындалады. Егер t және
-айнымалы
болса, онда бұл теңдеу бірыңғай орта
қозғалысы заңымен анықталады.
координатасы және t Лагранжа айнымалылары деп аталады.
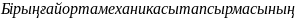 негізі
(1.1) формауласымен анықталады.
негізі
(1.1) формауласымен анықталады.
Механикада Ньютонның инерциалды жүйесі координаттары маңызды орын алады, олар бір-біріне тепе-тең және бірдей қозғалады. Ньютонның барлық заңдылықтары инерциалды жүйеде қалыптасады және оның таңдауынан тәуелсіз болып келеді.
Бірыңғай ортаның қозғалысын қарастырғанда, жүйеге сәйкес келетін координата жүйелері қарастырылады. (1.1)[2,3].
Егер бастапқы уақытта бірыңғай ортада сызықтық координаталарын таңдап, олар континуума нүктелерінен тұратын және уақыт өзгереді.
Жүйе қозғалады, созылады, айналады. Сәйкес келетін жүйенің координаталары жалпылама түсінік береді, шынайы жүйенің координаталары қатты дене теориялық механикада деформациялық ортаның бірыңғайлығы түсіндіреді.
Тәуелсіз айнымалы ретінде қолданылуы, бірыңғай ортаның қозғалысын зерттеу үшін лагранжен әдісін қолданады. Ол бірыңғай ортаның әрбір нүктесінің қозғалысының тарихы сипатына сүйенеді. Осындай анықтамалар механика заңдылығында нақты тапсырмаларда тым анық және қиын болып көрінеді.
Радиус вектор нүктесі арқылы жалпы бағыты және уақыты тәуелді болып келеді. Декоративтік жүйеде х координтасы әрқашан мүмкін болады. Онда жеке бірыңғай оратсы нүктесі үшін яғни бекітілген ξ үшін r –дың t-ға қатынасын көрсетеді:
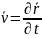 (1.2)
(1.2)
Жылдамдық жүйенің санағына байланысты есептеледі. Сәйкес бірыңғай жүйе координаталарына орнату сәйкесінше нөлге тең болады.
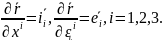 (1.3)
(1.3)
Мұндағы i, e – жүйені санайтын вектро базисі және ілесу жүйесі болып табылады.
Анықтама бойынша, υ келесі формула бойынша есептеледі
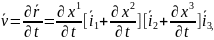 (1.4)
(1.4)
Ал жылдамдату келесі формула бойынша
 1.5)
1.5)
Қосымшада негізінде қозғалысты сипаттау үшін эйлер әдісін қолданады.Xжәне t айнымалылары Эйлер айнымалаылары деп аталды. Қайталанатын индекстер бойынша суммаларды қосып есептеу жүргізіледі.
Өріс шамалары r,v,a және x,t функция сияқты берілген, олар бекітілген х және t айнымалылары кеңістіктегі нүкте үшін әр түрлі бөлектер үшін өзгеруін анықтайды. Бекітілген және айнымалары кеелсіндей функциялары беретін белгілі t уақыттағы қозғалыс сипаттамасын береді. Х және t айнымалылары үшін әр уақыттағы кеңістіктегі қозғалыстарды анықтайды.
Сайып келгенде, лагранж әдісінде бірыңғай ортадағы жеке нүкте үшін өріс шамаларының өзгеру заңдылығын зерттейді, ал эйлер әдісінде нақты бір нүктедегі өріс шамаларының өзгеру заңдылығын анықтайды. Эйлер әдісінде кеңістіктің белгілі бір аумағы айқындалады және сол арқылы жеке бөліктердің өту қозғалысы зерртеледі. Матиматекалық тұрғыдан лагранж әдісінен айырмашылығы, біріншіден, х және t айнымалылары кеңістіктегі нүктенің координаталары болып табылады, ал екінші ξ параметрі.
Жалпы айтқанда бірыңғай орта қозғалысы заңдылығ келесідей түрге ие
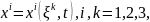 (1.6)
(1.6)
Мұнда ξ, t – Лагранж айнымалылары; х – Эйлер айнымалысы.
Сайып
келгенде, егер қозғалыс Лагранж айгымалысы
мен Эйлер айнымалысына өту үшін қозғалыс
заңын шешу керек, яғни (1.6)
 қатысты, оны (1.7) түрінде жазу керек.
қатысты, оны (1.7) түрінде жазу керек.
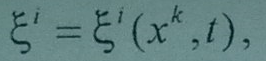 (1.7)
(1.7)
Лагранж арқылы Эйлер қозғалысына өту тек күңгірт функциялары арқылы өтеді.
Енді Эйлер айнымалыларының Лагранж айнымалысына өтуін қарастырайық. Тек Эйлер айнымалыларында жылдамдықтары берілген болсын
U = u(x ,y, z, t), v = v(x, y, z, t), w = w(x, y, z, t), (1.8)
U
=
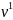 ,
v =
,
v =
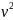 ,
x =
,
x =
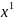 ,
y =
,
y =
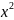 ,
z =
,
z =
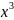 .
.
Анықтама бойынша,
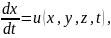
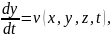 (1.9)
(1.9)
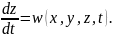
Х,
y,
z
қатысы дифференциалды теңдеуді шеше
отырып,
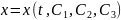 ,
,
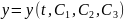 ,
,
 .
Мұнда,
.
Мұнда,
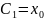 ,
,
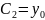 ,
,
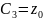 Лагранж
айнымалылары болып табылады. Қорытындылай
келе, дифференциалды теңдеуді шеше
отырып, қозғалыс заңын Эйлер айнымалысынан
Лагранж айнымалысына өту арқылы анықтай
аламыз. Байқағанымыздай, Эйлер
айнымалысынан Лагарнж айнымалысына
өту кезінде дифференциалдық теңдеудің
қарапайым интегралды жүйесі жылдамдығына
байланысты.
Лагранж
айнымалылары болып табылады. Қорытындылай
келе, дифференциалды теңдеуді шеше
отырып, қозғалыс заңын Эйлер айнымалысынан
Лагранж айнымалысына өту арқылы анықтай
аламыз. Байқағанымыздай, Эйлер
айнымалысынан Лагарнж айнымалысына
өту кезінде дифференциалдық теңдеудің
қарапайым интегралды жүйесі жылдамдығына
байланысты.
Бірыңғай ортадағы қозғалыс тапсырмасы көзқарасымен Лагранж және Эйлер механикалық қатынаста бір-біріне экивалентті.
