Лекция 1 элементы и параметры электрических цепей

1.1 Электрическая цепь. Элементы электрической цепи

Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Электромагнитные процессы в электрической цепи можно описать с помощью понятий «ток», «напряжение», «ЭДС», «сопротивление» («проводимость»), «индуктивность», «емкость».

Элемент электрической цепи — отдельное устройство, входящее в состав электрической цепи, выполняющее в ней определенную функцию. Элементы электрической цепи разделяют на источники электромагнитной энергии и приемники этой энергии. К элементам электрической цепи относятся также устройства для передачи и преобразования электромагнитной энергии.

Источниками электрической энергии являются химические источники тока, термоэлементы, генераторы и другие устройства, в которых происходит процесс преобразования химической, тепловой, механической или другого вида энергии в электрическую. В качестве источников электрической энергии могут быть источник ЭДС или источник тока. Часто встречаются сложные электрические цепи, в которых имеются как источники ЭДС, так и источники тока.

Приемниками электрической энергии (нагрузкой) называют устройства, в которых электрическая энергия преобразуется в другой вид энергии: световую, тепловую, механическую. Это электрические лампы, электронагревательные приборы, электрические двигатели и другие устройства. Все приемники электрической энергии можно представить в виде таких элементов электрической цепи, как резистор, катушка индуктивности, конденсатор.

Передающими электрическую энергию элементами цепи являются провода, линии электропередачи, коммутирующие аппараты, аппараты защиты.

Преобразование электромагнитной энергии осуществляется с помощью трансформаторов, изменяющих напряжение и ток, преобразователей частоты, усилителей, а также инверторов, преобразующих постоянный ток в переменный, выпрямителей, преобразующих переменный ток в постоянный, и т.п.

Резистор — элемент электрической цепи, предназначенный для использования его электрического сопротивления. Параметром резистора является его электрическое сопротивление. Электрическое сопротивление резистивного элемента (R) определяется по формуле:

,

где ρ — удельное электрическое сопротивление материала резистора;

l и S — соответственно длина и площадь сечения резистора.

В резисторе (реостате, нагревательном элементе и т.п.) происходит преобразование электрической энергии в тепловую. Падение напряжения на резисторе u можно выразить через величину его сопротивления и ток, протекающий по резистору i: u = iR — а ток —

i = .

Индуктивная катушка — элемент электрической цепи, предназначенный для использования его индуктивности. В этом электротехническом устройстве накапливается энергия магнитного поля. Параметром индуктивной катушки является индуктивность. Индуктивность катушки (L) определяют по формуле:

,

где μ_а — абсолютная магнитная проницаемость материала сердечника катушки;

W — число витков катушки;

l_cp, S — соответственно длина средней линии и площадь

сечения сердечника.

При протекании тока по проводнику вокруг него возникает магнитное поле. Если это индуктивная катушка, то за счет наличия витков имеет место потокосцепление. Потокосцепление Из курса физики известно, что, согласно закону электромагнитной индукции, ЭДС индукции

.

Проинтегрировав выражение:

,

— получим зависимость изменения тока на индуктивной катушке во времени:

В последнем выражении i(0) есть начальное значение тока при t = 0. Если в начальный момент времени при t = 0 i(0) = 0, то изменение тока на катушке можно записать в следующем виде:

.

Конденсатор — элемент электрической цепи, предназначенный для использования его емкости. В емкостном элементе накапливается энергия электрического поля. Параметром конденсатора является его электрическая емкость. Емкость плоского конденсатора (С) определяют по формуле:

C = ε_a ,

где ε_a — диэлектрическая проницаемость изоляционного материала

между электродами конденсатора;

S, d — соответственно площадь электрода и расстояние между

электродами.

Известно, что величина заряда (q), который накапливает конденсатор, прямо пропорциональна приложенному к нему напряжению и его емкости: q = Cu_C. Так как dq = idt, то ток, протекающий через конденсатор при его зарядке,

i = C .

Выразив из полученной формулы изменение напряжения на конденсаторе и проинтегрировав его, получим:

,

где u_C(0) — значение напряжения на конденсаторе в момент

времени t = 0.

Если u_C(0) = 0, то напряжение на конденсаторе

.

Итак, соотношения между мгновенными значениями напряжений и токов на участках цепи с элементами R, L, C следующие:

; ; ;

; ; .

Классификация электрических цепей. Электрические цепи классифицируют по следующим основным признакам:

- количеству источников энергии (простые и сложные);

- конструкции (неразветвленные, разветвленные);

- роду тока (постоянного, переменного);

- числу фаз (одно-, трех-, многофазные);

- виду вольт-амперной характеристики элементов цепи (линейные, нелинейные);

- форме кривой напряжения, ЭДС или тока (синусоидальные, несинусоидальные);

- по распределению параметров элементов электрической цепи вдоль ее длины (цепи с сосредоточенными параметрами и цепи с распределенными параметрами) и т. п.

Электрические цепи с одним источником энергии независимо от количества потребителей называются простыми, а цепи с двумя и более источниками энергии — сложными.

Электрические цепи, в которых получение электрической энергии в источниках, ее передача и преобразование в приемниках происходят при неизменных во времени напряжениях и токах, называют цепями постоянного тока. В цепях постоянного тока не возникают ЭДС индукции и отсутствуют токи смещения в диэлектриках, окружающих проводники.

На практике обычно приемник или элемент цепи представляют вольт-амперной характеристикой U(I) — зависимостью напряжения, например, на резисторе от величины протекающего через него тока. Вольт-амперные характеристики, сокращенно ВАХ, могут быть нелинейными (рисунок 1.2) и линейными (рисунок 1.3). Соответственно, электрические цепи, содержащие элементы с нелинейными характеристиками, называют нелинейными, а цепи, содержащие только элементы с линейными характеристиками, называют линейными.

Для нелинейных резистивных элементов характерно, что сопротивление зависит от тока. Так, судя по ВАХ (рисунок 1.2), сопротивление элемента 1 падает с ростом тока, а сопротивление элемента 2 — растет. Режимы работы большого числа реальных электрических цепей можно отнести к линейным (рисунок 1.3), поэтому изучение свойств и методов расчета линейных электрических цепей представляет значительный практический интерес.

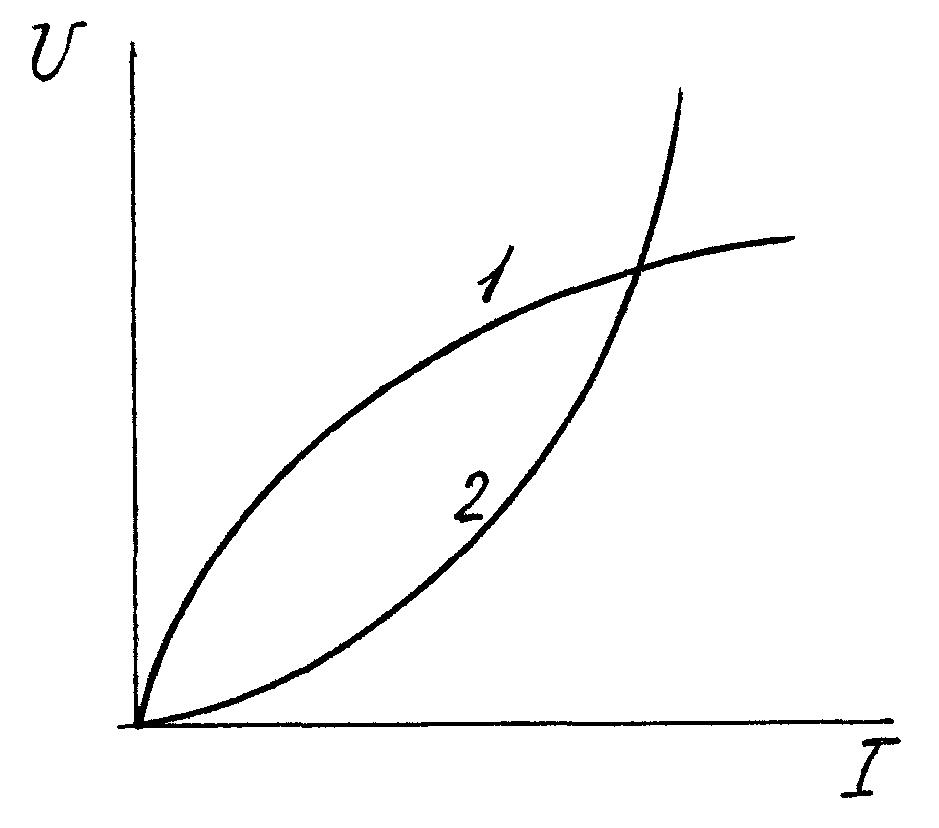
Рисунок 1.2 — ВАХ нелинейных элементов электрической цепи

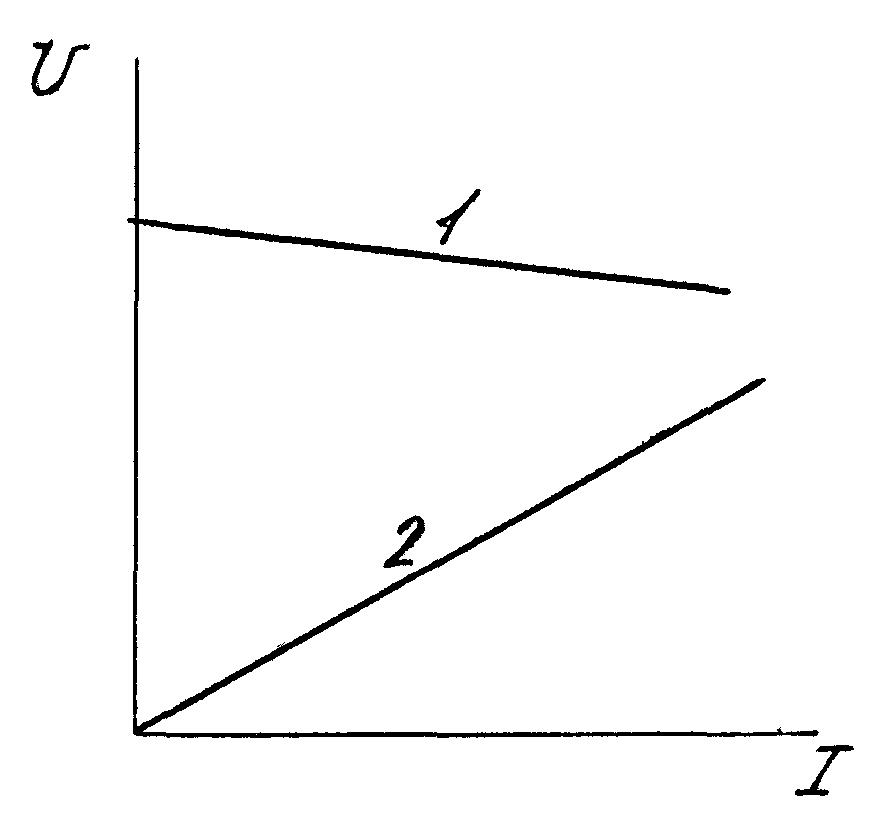
Рисунок 1.3 — ВАХ линейных элементов электрической цепи

Электрическую цепь, в которой электрические сопротивления, индуктивности и электрические емкости считаются сосредоточенными на отдельных участках этой цепи, называют электрической цепью с сосредоточенными параметрами. А электрическая цепь, в которой электрические сопротивления, проводимости, индуктивности и электрические емкости распределены вдоль цепи, называется электрической цепью с распределенными параметрами. Примером цепи с распределенными параметрами могут служить протяженные линии электропередачи, линии связи, катушки индуктивности с большим числом витков и т.д. Как правило, если не указывается, что электрическая цепь с распределенными параметрами, то она считается цепью с сосредоточенными параметрами и это не подчеркивается.

Примеры классификации электрических цепей по другим признакам студенты могут привести самостоятельно.

Элементы электрической цепи могут быть соединены последовательно, параллельно, смешанно, по схемам «звезда», «треугольник».

Последовательным соединением участков электрической цепи называют такое соединение, при котором через все участки цепи проходит один и тот же ток.

При последовательном соединении резистивных элементов R₁, R₂, R₃, …, R_n эквивалентное сопротивление R_э равно сумме сопротивлений:

.

Параллельным соединением участков цепи называют такое соединение, при котором все участки присоединены к одной паре узлов, эти участки находятся под действием одного и того же напряжения.

Параллельно соединенные резистивные элементы R₁, R₂, R₃, …, R_n можно заменить одним эквивалентным с проводимостью:

g_э  =  g₁ + g₂ + g₃ + …+g_n,

где g_э = ; g₁ = ; g₂ = ; g₃ = _; g_n = .

Для двух параллельно соединенных резисторов

R_э =  .

При смешанном соединении участков электрической цепи имеются участки с последовательным и параллельным соединением (рисунок 1.4).

Рисунок 1.4 — Электрическая цепь со смешанным соединением элементов

Расчет токов в схеме со смешанным соединением участков цепи с резистивными элементами проводят путем последовательных преобразований цепи и сведения всех резистивных элементов к одному с эквивалентным сопротивлением. При этом должны быть заданы величины сопротивлений и напряжение или ЭДС на входе цепи. Например, для схемы рисунка 1.4 преобразование проводят следующим образом.

Параллельно соединенные участки заменяют одним эквивалентным, имеющим проводимость

откуда

После такого преобразования схема будет состоять из двух последовательно соединенных участков с сопротивлениями R₁ и R₂₃₄ (рисунок 1.5). Эквивалентное сопротивление цепи R_э = R₁ + R₂₃₄.

U

Рисунок 1.5 — Электрическая цепь после преобразования

Свойства электрических цепей

Знание отдельных свойств электрических цепей позволяет в некоторых случаях упростить как расчет электрической цепи, так и ее экспериментальное исследование. Эти свойства часто именуются теоремами или принципами. К ним относятся принцип наложения, принцип взаимности, принцип компенсации, принцип эквивалентного генератора и др. Справедливость этих принципов вытекает из анализа уравнений, составленных по законам Кирхгофа.

Принцип наложения. Ток в любой ветви сложной электрической цепи равен алгебраической сумме токов, вызываемых каждой ЭДС в отдельности. Принцип наложения используется в методе расчета, получившем название метода наложения. При расчете цепей по методу наложения поступают следующим образом: поочередно рассчитывают токи от каждой ЭДС, считая все остальные ЭДС источников равными нулю, но сохраняя в схеме их внутренние сопротивления. Ток в любой ветви определяется путем алгебраического суммирования частичных токов.

Принцип взаимности. Если ЭДС Е, действуя в ветви ab сколь угодно сложной цепи, при отсутствии в цепи прочих ЭДС, вызывает в другой ветви cd этой цепи ток I, то эта же ЭДС E, действуя в ветви cd, при отсутствии прочих ЭДС, вызовет в ветви ab такой же ток I.

Принцип взаимности в сочетании с принципом наложения дает возможность существенно снизить трудоемкость расчета сложной цепи, в которой действуют одновременно несколько ЭДС, особенно в случае, когда требуется определить ток в одной ветви этой цепи.

Принцип эквивалентного генератора. Ток в некоторой ветви ab с сопротивлением Z_ab не изменится, если всю остальную цепь, содержащую источники ЭДС, заменить эквивалентным генератором с ЭДС, равной напряжению на зажимах ab при разомкнутой ветви (при холостом ходе), и внутренним сопротивлением, равным входному сопротивлению Z₁ цепи относительно зажимов ab при разомкнутой ветви ab и замкнутых накоротко источниках ЭДС. Ток I в ветви ab в схеме цепи с эквивалентным генератором находится из выражения:

.

Напряжение Е_Г и входное сопротивление Z₁ определяются экспериментальным или расчетным путем.