3.20 Экспериментальное определение коэффициентов четырехполюсника

Комплексные коэффициенты четырехполюсника A, B, C, D могут быть определены расчетным путем согласно формулам (3.89). Для этого должны быть известны сопротивления или проводимости ветвей внутренней цепи четырехполюсника.

Для экспериментального определения коэффициентов четырехполюсника необходимо выполнить три опыта. В каждом из этих опытов подключают четырехполюсник к источнику синусоидального напряжения и измеряют ток, напряжение и мощность.

1. Опыт холостого хода при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' разомкнуты.

По показаниям приборов определим входное сопротивление:

.

Сопротивление, напряжение и ток в этом опыте записываются с дополнительным индексом «10». Уравнения четырехполюсника в условиях данного опыта имеют вид:

; .

Следовательно, . (3.96)

2. Опыт короткого замыкания при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' замкнуты накоротко.

По показаниям приборов определяем входное сопротивление (дополнительный индекс «1K»):

.

Уравнения четырехполюсника имеют вид:

; .

. (3.97)

3. Опыт короткого замыкания при питании со стороны зажимов 2 и 2', . Зажимы 1 и 1' замкнуты накоротко.

По показаниям приборов определяем входное сопротивление (индекс «2K»):

.

Уравнения четырехполюсника для данного опыта (питание со стороны выхода) имеют вид:

; .

. (3.98)

Из уравнений (3.96), (3.97), (3.98) имеем:

; ; . (3.99)

Подставив значения B, C, D в уравнение , получим

,

откуда

. (3.100)

Определив по (3.100) значение A через Z₁₀, Z_1K, Z_1K, затем находят B, C, D. Согласно формулам (3.99), (3.100) коэффициенты A и D безразмерны, коэффициент B имеет размерность ом (Ом), коэффициент C — сименс (См).

В качестве третьего опыта вместо опыта короткого замыкания может быть сделан опыт холостого хода. Для экспериментального определения коэффициентов симметричного четырехполюсника достаточно двух опытов.

3.21 Эквивалентные схемы четырехполюсника

Пассивный четырехполюсник характеризуется четырьмя коэффициентами: A, B, C, D. Из них независимыми являются три, поскольку четвертый может быть определен из уравнения: . Поэтому простейшая эквивалентная схема четырехполюсника содержит три элемента. На рисунке 3.40 изображена так называемая Т-образная эквивалентная схема четырехполюсника, на рисунке 3.41 — П-образная схема четырехполюсника.

Рисунок 3.40 — Т-образная эквивалентная схема

Рисунок 3.41 — П-образная эквивалентная схема

Используя законы Кирхгофа, выразим напряжение и ток на входе Т-образной эквивалентной схемы через напряжение и ток на выходе (рисунок 3.40):

; .

; (3.101)

. (3.102)

Сопоставляя уравнения (3.101) и (3.102) с уравнениями четырехполюсника (3.82) и (3.83), получим:

; ; ; . (3.103)

Из последних выражений определяем сопротивления Т-образной эквивалентной схемы:

; ; .

Выразим напряжение и ток на входе через напряжение и ток на выходе П-образной эквивалентной схемы (рисунок 3.41):

; .

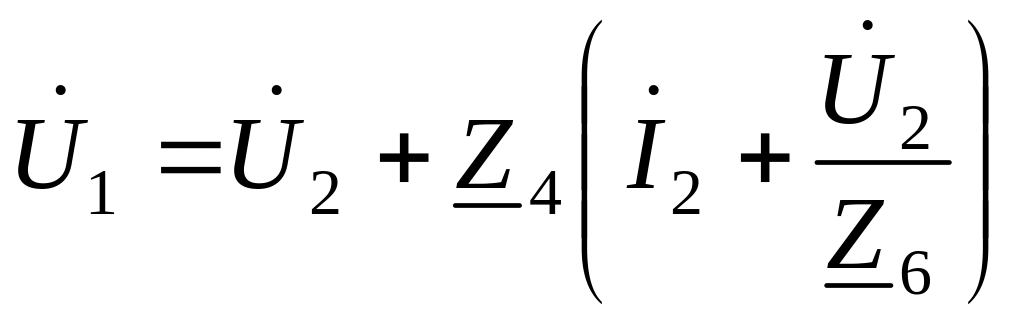; (3.104)

. (3.105)

Сопоставляя уравнения (3.104) и (3.105) с уравнениями четырехполюсника (3.82) и (3.83), получим:

; ; ; . (3.106)

Из последних выражений определяем сопротивления П-образной эквивалентной схемы:

; ; .

Если четырехполюсник симметричный, то и в Т-образной эквивалентной схеме , а в П-образной эквивалентной схеме .