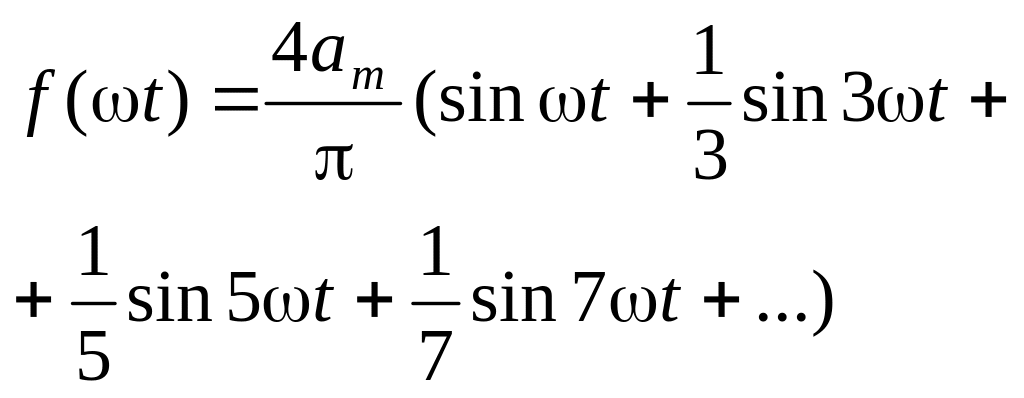- •Часть 1
- •Содержание
- •Модуль 0 введение в курс теоретических основ электротехники, цели и задачи дисциплины
- •Учебно-информационная модель изучения дисциплины
- •Учебно-информационная модель изучения дисциплины (Окончание)
- •Научно-теоретический материал
- •Модуль 1 основные понятия и законы электрических цепей вводный комментарий к модулю
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Продолжение)
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь основных понятий
- •Основы научно-теоретических знаний по модулю
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 элементы и параметры электрических цепей
- •1.1 Электрическая цепь. Элементы электрической цепи
- •1.2 Электрическая схема и схемы замещения источников энергии
- •1.3 Ток, напряжение, эдс, мощность, энергия
- •Лекция 2 законы электрических цепей и их применение
- •1.4 Закон Ома для участка цепи, содержащего эдс
- •1.5 Законы Кирхгофа
- •1.6 Энергетический баланс в электрической цепи
- •Лекция 3 основные понятия о цепях синусоидального тока
- •1.7 Общие сведения о цепях переменного тока
- •1.8 Величины, характеризующие синусоидальный ток. Генерирование синусоидальной эдс
- •1.9 Среднее и действующее значения синусоидального тока, напряжения, эдс
- •1.10 Изображение синусоидально изменяющихся величин векторами и комплексными числами. Векторные диаграммы
- •1.11 Синусоидальный ток в активном, индуктивном и емкостном элементах
- •Лекция 4 закон ома, законы кирхгофа для цепи синусоидального тока
- •1.12 Синусоидальный ток в цепи с последовательным соединением активного, индуктивного и емкостного элементов
- •1.13 Закон Ома, законы Кирхгофа для цепей синусоидального тока
- •Лекция 5 энергетические процессы в цепях синусоидального тока
- •1.14 Мгновенная мощность и колебания энергии в цепи синусоидального тока
- •1.15 Активная, реактивная и полная мощности. Баланс мощностей
- •1.16 Условие передачи максимальной активной мощности от источника к приемнику
- •Контрольные вопросы и задачи для самостоятельного изучения цепей постоянного тока
- •Контрольные вопросы и задачи для самостоятельного изучения цепей синусоидального тока
- •Материалы к практическим занятиям
- •Практическое занятие 1 Применение закона Ома для расчета токов и напряжений
- •Практическое занятие 2 Применение законов Кирхгофа для расчета цепей постоянного тока
- •Практическое занятие 3 Применение закона Ома, законов Кирхгофа для расчета цепей синусоидального тока
- •Практическое занятие 4 Электрические цепи переменного тока со смешанным соединением элементов
- •Практическое занятие 5 Мощности в цепях переменного напряжения
- •Материалы к лабораторным занятиям
- •Лабораторное занятие 1 Экспериментальная проверка законов Кирхгофа в цепях постоянного тока
- •Лабораторное занятие 2 Исследование цепи переменного напряжения с последовательным соединением приемников
- •Лабораторное занятие 3 Исследование электрической цепи с параллельным и смешанным соединением элементов
- •Лабораторное занятие № 4 Измерение мощности и определение параметров приемника в цепи переменного тока
- •Материалы к управляемой самостоятельной работе по разделу «Методы расчета простых цепей постоянного тока»
- •Материалы к управляемой самостоятельной работе по разделу «Расчет электрической цепи синусоидального тока со смешанным соединением приемников»
- •Образец контрольных заданий по модулю 1
- •Образец контрольных заданий по модулю 1 (Окончание)
- •Модуль 2 методы расчета электрических цепей вводный комментарий к модулю
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь понятий для повторения
- •Основы научно-теоретических знаний
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 методы расчета простых электрических цепей и использование при расчете их свойств и преобразований
- •2.1 Расчет простых цепей при последовательном, параллельном и смешанном соединениях приемников
- •2.1.1 Расчет цепи при последовательном
- •2.1.2 Расчет цепи при параллельном соединении приемников
- •2.1.3 Расчет цепи при смешанном соединении приемников
- •2.2 Преобразование соединения «треугольником» в эквивалентное соединение «звездой» и обратно
- •2.3 Использование при расчете свойств электрических цепей
- •Лекция 2 методы расчета сложных электрических цепей
- •2.4 Метод уравнений Кирхгофа
- •2.5 Метод контурных токов
- •2.6 Метод узловых потенциалов
- •2.7 Метод двух узлов
- •2.8 Метод эквивалентного генератора
- •2.9 Матричный метод расчета линейных электрических цепей (для самостоятельной работы)
- •2.9.1 Геометрия электрических цепей
- •2.9.2 Топологические матрицы схем
- •2.9.3 Законы Кирхгофа в матричной форме
- •2.9.4 Закон Ома в матричной форме
- •2.9.5 Матричные уравнения контурных токов
- •2.9.6 Матричные уравнения узловых потенциалов
- •3.9.7 Порядок расчета электрических цепей матричным методом
- •Контрольные вопросы и задачи для самостоятельного решения
- •Материалы к практическим занятиям
- •Практическое занятие 1 Методы расчета сложных электрических цепей (уравнения Кирхгофа, контурных токов, узловых потенциалов)
- •Практическое занятие 2 Методы расчета сложных электрических цепей — 2-х узлов, эквивалентного генератора
- •Практическое занятие 3 Дополнение к методам расчета сложных цепей
- •Материалы к лабораторным занятиям Лабораторное занятие 1 Исследование свойств электрических цепей
- •Материалы к управляемой самостоятельной работе студентов
- •Образец контрольных заданий по модулю 2
- •Образец контрольных заданий по модулю 2 (Окончание)
- •Учебно-информационная модель изучения модуля
- •Учебно-информационная модель изучения модуля (Окончание)
- •Словарь основных понятий
- •Основы научно-теоретических знаний
- •Материалы, используемые в процессе обучения Материалы к лекциям
- •Лекция 1 резонансные явления в электрических цепях
- •3.1 Основные понятия о резонансе в электрических цепях
- •3.2 Резонанс напряжений
- •3.3 Частотные характеристики последовательного колебательного контура
- •3.4 Резонанс токов
- •3.5 Частотные характеристики параллельного контура
- •3.6 Компенсация сдвига фаз
- •3.7 Понятие о резонансе в разветвленных электрических цепях
- •Контрольные вопросы и задачи для самостоятельной работы
- •Вопросы для самоконтроля
- •Лекция 2 цепи со взаимной индуктивностью
- •3.8 Индуктивно-связанные элементы цепи
- •3.9 Электродвижущая сила взаимной индукции
- •3.10 Расчет электрических цепей при наличии индуктивно-связанных элементов
- •3.10.1 Последовательное соединение двух индуктивно-связанных катушек
- •3.10.2 Параллельное соединение двух индуктивно-связанных катушек
- •3.11 Опытное определение взаимной индуктивности
- •3.12 Воздушный трансформатор
- •Контрольные вопросы и задачи для самостоятельного решения
- •Лекция 3 несинусоидальные периодические эдс, напряжения и токи Общие сведения
- •3.12 Разложение периодической несинусоидальной кривой в тригонометрический ряд
- •3.13 Расчет мгновенных значений напряжений и токов в электрических цепях при действии периодических несинусоидальных эдс
- •3.14 Действующие значения периодических несинусоидальных токов, напряжений и эдс
- •3.15 Мощность в цепи несинусоидального тока
- •3.16 Замена несинусоидальных токов и напряжений эквивалентными синусоидальными
- •3.17 Зависимость формы кривой тока от характера цепи при несинусоидальном напряжении
- •Лекция 4 четырехполюсники
- •3.19 Четырехполюсники и их уравнения
- •3.20 Экспериментальное определение коэффициентов четырехполюсника
- •1. Опыт холостого хода при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' разомкнуты.
- •2. Опыт короткого замыкания при питании со стороны зажимов 1 и 1', . Зажимы 2 и 2' замкнуты накоротко.
- •3. Опыт короткого замыкания при питании со стороны зажимов 2 и 2', . Зажимы 1 и 1' замкнуты накоротко.
- •3.21 Эквивалентные схемы четырехполюсника
- •3.22 Характеристическое сопротивление и коэффициент передачи четырехполюсника
- •3.23 Электрические фильтры
- •Материалы к практическим занятиям
- •Практическое занятие 1 Резонанс в электрических цепях
- •Задачи для самостоятельного решения
- •Индивидуальные задания
- •Практическое занятие 2 Индуктивно-связанные цепи
- •Практическое занятие 3 Цепи с несинусоидальными токами
- •Практическое занятие 4 Мощность в цепи несинусоидального тока
- •Практическое занятие 5 Четырехполюсники
- •Материалы к лабораторным занятиям Лабораторная работа 1 Резонанс токов и компенсация сдвига фаз
- •Лабораторная работа № 2 Исследование режимов работы четырехполюсника
- •Материалы к управляемой самостоятельной работе студентов
- •Образец контрольных заданий по модулю 3
- •Образец контрольных заданий по модулю 3 (Окончание)
- •Задание для усрс
- •Литература Основная
- •Дополнительная
- •Теоретические основы электротехники
- •Часть 1
- •220023, Г. Минск, пр. Независимости, 99, к. 2.
3.12 Разложение периодической несинусоидальной кривой в тригонометрический ряд
Как известно, всякая периодическая функция f(ωt), удовлетворяющая условиям Дирихле, т.е. имеющая на каждом конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд Фурье. Периодические несинусоидальные ЭДС, напряжения и токи в реальных электрических цепях удовлетворяют условиям Дирихле. Поэтому, например, для периодической несинусоидальной ЭДС можно написать:
e(t) = E0 + E1msin(ωt + ψ1) + E2msin(2ωt + ψ2) + E3msin(3ωt + ψ3) + … +
+
Ekmsin(kωt
+ ψk)
+ … = E0
+
![]() .
(3.60)
.
(3.60)
Первый член ряда E0 называется постоянной составляющей ЭДС, или нулевой гармоникой, второй член E1msin(ωt + ψ1) — основной синусоидой, или первой гармоникой, а все остальные члены ряда вида Ekmsin(kωt + ψk) при k > 1 носят название высших гармоник.
В последнем
выражении k
— номер гармоники. Он показывает, во
сколько раз частота k-гармоники
больше основной частоты. Основная
угловая частота
![]() ,
где T
— период несинусоидальной периодической
ЭДС.
,
где T
— период несинусоидальной периодической
ЭДС.
В общем случае ряд Фурье содержит бесконечное число членов, но, как правило, можно ограничиться некоторым конечным числом членов ряда.
Для вычисления коэффициентов ряда Фурье целесообразно его члены представить через синусоиды и косинусоиды без начальных фаз. Имеем
Ekmsin(kωt + ψk) = Ekmcosψksinkωt + Ekmsinψkcoskωt =
= Bkmsinkωt + Ckmcoskωt.
Таким образом,
e(t)
= E0
+
![]() .
(3.61)
.
(3.61)
Постоянная составляющая E0 и коэффициенты Bkm и Ckm, как известно из курса математики, определяются с помощью формул:
![]() ;
;
Bkm
=
![]() ;
(3.62)
;
(3.62)
Ckm
=
![]() .
.
Имея Bkm и Ckm, нетрудно вычислить амплитуду и начальную фазу k-гармоники:
![]() ;
ψk
= arctg
;
ψk
= arctg![]() .
(3.63)
.
(3.63)
Аналогично можно разложить в ряд Фурье несинусоидальные токи и напряжения.
Разложение в ряд Фурье встречающихся в электротехнике периодических кривых геометрически правильной формы приведено в справочных таблицах.
В таблице 3.1 даны разложения в тригонометрический ряд некоторых простейших функций.
Таблица 3.1 — Разложение периодических функций в ряд Фурье
№ |
График f(ωt) |
Разложение в ряд f(ωt) |
1 |
|
|
2 |
|
|
Окончание таблицы 3.1
№ |
График f(ωt) |
Разложение в ряд f(ωt) |
3 |
|
f(ωt)
= =
|
4 |
|
f(ωt)
=
|
Для кривых геометрически неправильной формы, заданных в виде графика, применяют графоаналитический метод определения гармоник тригонометрического ряда [1].
3.13 Расчет мгновенных значений напряжений и токов в электрических цепях при действии периодических несинусоидальных эдс
Если в линейной цепи действует один или несколько источников несинусоидальных периодических ЭДС, то расчет токов цепи распадается на три этапа.
1. Разложение ЭДС источников в тригонометрический ряд, то есть на постоянную и синусоидальные составляющие. Это означает, что источник несинусоидальной ЭДС можно рассматривать как последовательное соединение источника постоянной ЭДС и источников синусоидальных ЭДС с различными частотами. Так, если ЭДС (рисунок 3.32, а)
e = E0 + E1msin(ωt + ψ1) + E2msin(2ωt + ψ2), (3.64)
то действие источника такой ЭДС аналогично действию трех последовательно соединенных источников ЭДС (рисунок 3.32, б):
![]() ;
e1
= E1msin(ωt
+ ψ1);
e2
= E2msin(2ωt
+ ψ2).
;
e1
= E1msin(ωt
+ ψ1);
e2
= E2msin(2ωt
+ ψ2).


а) б)
Рисунок 3.32 — Замена источника несинусоидальной ЭДС последовательным соединением источников постоянной и синусоидальной ЭДС
2. Расчет мгновенных значений токов, возникающих в ветвях электрической цепи под действием каждой из составляющих несинусоидальной ЭДС в отдельности.
3. Нахождение мгновенных значений токов в ветвях в соответствии с принципом наложения в виде суммы мгновенных значений составляющих токов.
Если, например, в какой-либо ветви токи, создаваемые ЭДС E0, e1 и e2, соответственно равны I0, i1 и i2, то общий ток ветви
![]() .
.
Таким образом, расчет линейной цепи с несинусоидальными ЭДС сводится к решению n задач с синусоидальными ЭДС, где n — число синусоидальных составляющих ЭДС различных частот, и одной задачи с постоянными ЭДС.
При решении каждой из этих задач необходимо учитывать, что для различных частот индуктивные и емкостные сопротивления неодинаковы. Индуктивное сопротивление для k-гармоники в k раз больше, а емкостное, наоборот, в k раз меньше, чем для первой:
XLk = kωL = kXL1;
XCk
=
![]() .
.
Для постоянной составляющей E0 индуктивное сопротивление равно нулю, а емкостное — бесконечности. Активное сопротивление также зависит от частоты — увеличивается с ростом последней вследствие поверхностного эффекта. Если расчет ведется для гармоник невысоких частот и относительно малых сечений проводов, можно не учитывать изменения сопротивления R с частотой и считать, что при всех частотах активное сопротивление равно сопротивлению при постоянном токе.
Так как каждая составляющая тока является либо постоянной величиной, либо синусоидальной функцией времени, то для расчета каждой из них в отдельности могут быть применены все методы, рассмотренные для расчета цепей постоянного и синусоидального токов. Целесообразно для расчета каждой синусоидальной составляющей в отдельности использовать комплексный метод. Закон Ома в комплексной форме для k-гармоники имеет вид:
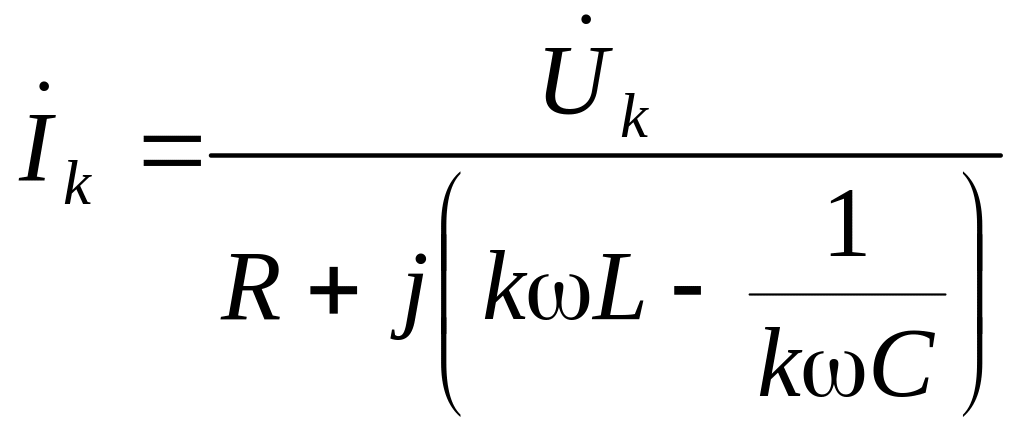 .
(3.65)
.
(3.65)
Суммировать полученные комплексы токов для отдельных гармоник нельзя, так как они имеют разные частоты. Суммировать можно лишь мгновенные значения, выраженные как функции времени.
Пользуясь этим методом, определим ток i в простейшей неразветвленной цепи с постоянными параметрами R, L, C (рисунок 3.33) при установившемся режиме в случае, когда напряжение u на зажимах цепи является периодической несинусоидальной функцией времени. Представим напряжение в виде ряда:
![]() ,
,
где U0 — постоянная составляющая;
uk = Ukmsin(kωt + ψuk) — k-гармоника.

Рисунок 3.33 — Электрическая цепь при действии периодического несинусоидального напряжения
Постоянная составляющая тока в этой цепи равна нулю, то есть I0 = 0, так как конденсатор постоянного тока не проводит.
Синусоидальные составляющие тока, возникающие в цепи под действием каждой синусоидальной составляющей напряжения разных частот, найдем, используя закон Ома в комплексной форме. Рассчитаем комплексную амплитуду тока k-гармоники:
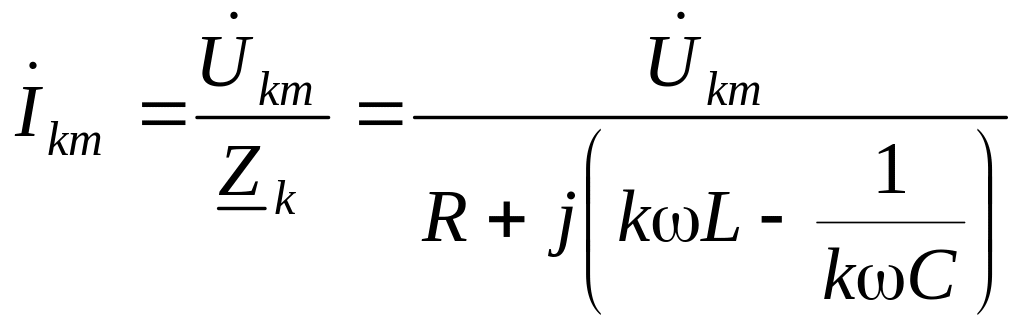 .
(3.66)
.
(3.66)
Записываем
![]() и
и
![]() ,
причем
,
причем
![]() и φk = arctg
и φk = arctg ,
получим
,
получим
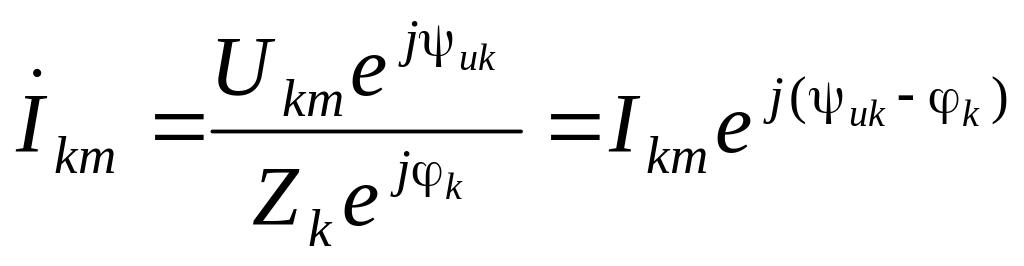 .
.
Мгновенное значение тока k-гармоники тока имеет вид:
ik = Ikmsin(kωt + ψuk – φk) = Ikmsin(kωt + ψik).
Искомый ток определяется суммой:
![]() .
.
Для наглядного представления о форме кривой несинусоидального тока необходимо рисовать графики отдельных гармоник и результирующей кривой, полученной суммированием ординат составляющих токов. При вычерчивании кривых отдельных гармоник следует всегда иметь в виду, что период гармоники обратно пропорционален ее номеру. Следовательно, если по оси абсцисс отложено ωt, то, соблюдая один и тот же масштаб, вместо углов ψk надо откладывать углы ψk/k. В качестве примера построим график несинусоидального тока, состоящего из двух гармоник (рисунок 3.34):
i = 12sin(ωt + 120°) + 4sin(2ωt + 90°) А.

Рисунок 3.34 — Построение графика несинусоидального тока
При построении графика тока второй гармоники i2 учтено, что период этой гармоники в 2 раза меньше периода тока первой гармоники i1 и начальная фаза второй гармоники (90°) разделена на номер гармоники (90°/2 = 45°).