Вопросы для самоконтроля

1 Что понимают под колебательным контуром?

2 Чему равна угловая частота собственных колебаний колебательного контура?

3 Что понимают под резонансом в электрической цепи?

4 В какой цепи, при каких условиях возникает резонанс напряжений?

5 В какой цепи, при каких условиях возникает резонанс токов?

6 Какую опасность могут представлять резонансные контуры в электрических цепях?

7 Что понимают под компенсацией сдвига фаз и как ее осуществляют?

8 Какие контуры (катушки) называют индуктивно-связанными?

9 Как опытно определить одноименные выводы катушек и их взаимоиндуктивность?

10 Каковы методы расчета индуктивно-связанных цепей?

11 Каковы условия передачи максимальной мощности от источника к приемнику?

12 Что понимают под падением и потерей напряжения?

13 На чем основан метод расчета цепей несинусоидального напряжения и как он реализуется?

14 Как определить действующее значение несинусоидального тока, напряжения, ЭДС?

15 Как определяют мощности цепей несинусоидального напряжения?

16 Что понимают под электрическими фильтрами и на чем основан их принцип действия?

17 В чем суть теории четырехполюсников?

Лекция 2 цепи со взаимной индуктивностью

3.8 Индуктивно-связанные элементы цепи

Электрические цепи, в которых изменение тока в одной из ветвей может вызвать появление ЭДС в другой ветви, называют индуктивно-связанными, или цепями со взаимной индукцией. Возникающую в этом случае ЭДС называют ЭДС взаимной индукции.

Рассмотрим две катушки, расположенные на некотором расстоянии друг от друга (рисунок 3.14).

Рисунок 3.14 — Магнитная связь между двумя катушками

Пусть по обмотке первой катушки протекает ток i₁, в результате чего возникает магнитный поток, часть которого Φ₁₁ будет связана с витками своей катушки 1, часть магнитного потока Φ₁₂ пронизывает витки второй катушки.

Потокосцепление первой катушки со второй ψ₁₂ в случае неферромагнитной среды

ψ₁₂ = W₂Φ₁₂, (3.22)

где W₂ — число витков второй катушки.

Если по обмотке второй катушки проходит ток i₂, то создается магнитный поток, часть которого Φ₂₁ будет пронизывать витки обмотки первой катушки и образует потокосцепление ψ₂₁,

ψ₂₁ = W₁Φ₂₁, (3.23)

где W₁ — число витков первой катушки.

Отношение потокосцепления второго контура (катушки) ψ₁₂ к силе тока, возбуждающего это потокосцепление i₁, называют взаимной индуктивностью контуров:

M₁₂ = = . (3.24)

Аналогично

M₂₁ = = . (3.25)

Для двух контуров всегда имеет место равенство на основании принципа взаимности, а именно: M₁₂ = M₂₁ = M, — поэтому необходимость в написании индексов отпадает. Взаимная индуктивность измеряется в генри (Гн).

Магнитный поток взаимоиндукции является частью потока одного из контуров, поэтому взаимная индуктивность, как и индуктивность, зависит от свойств материалов магнитной цепи, геометрических параметров, числа витков обмоток катушек, а также от их взаимного расположения.

Магнитная связь между двумя контурами характеризуется коэффициентом связи.

Отношение потока Φ₁₂ ко всему потоку Φ₁₁

. (3.26)

Аналогично

, (3.27)

где L₁ и L₂ — индуктивность первой и второй катушек.

Каждое из отношений (3.26), (3.27) показывает, какая часть потока, созданного током одной катушки, сцепляется с другой.

Среднее геометрическое этих отношений представляет собой коэффициент, или степень индуктивной связи k двух катушек.

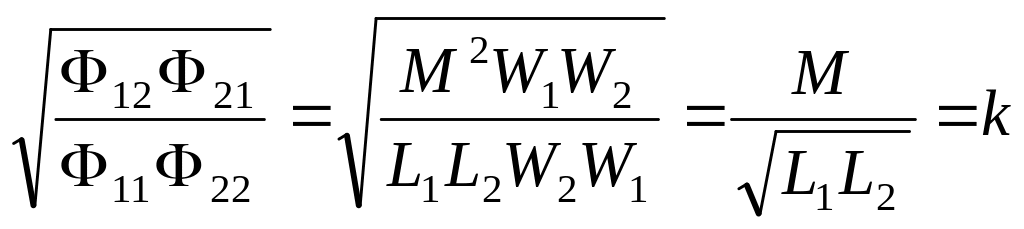. (3.28)

Так как магнитный поток Φ₁₁ больше, чем магнитный поток Φ₁₂, а Φ₂₂ больше магнитного потока Φ₂₁, то коэффициент связи всегда меньше единицы: k < 1.