3.4 Резонанс токов

Резонанс токов возможен в цепи синусоидального напряжения, состоящей из двух ветвей, обладающих индуктивностью и емкостью (рисунок 3.6).

Рисунок 3.6 — Схема параллельного колебательного контура

Такую цепь иногда называют параллельным колебательным контуром. Резонанс в такой цепи наступит, когда реактивная проводимость цепи будет равна нулю, b = b_C – b_L = 0, из чего следует, что условием резонанса будет являться равенство емкостной и индуктивной проводимости: b_C = b_L. Комплексная полная проводимость первой ветви

Y₁ = , (3.15)

где = b_L — индуктивная проводимость;

= g₁ — активная проводимость первой ветви.

Комплексная полная проводимость второй ветви

Y₂ = , (3.16)

где = b_C — индуктивная проводимость;

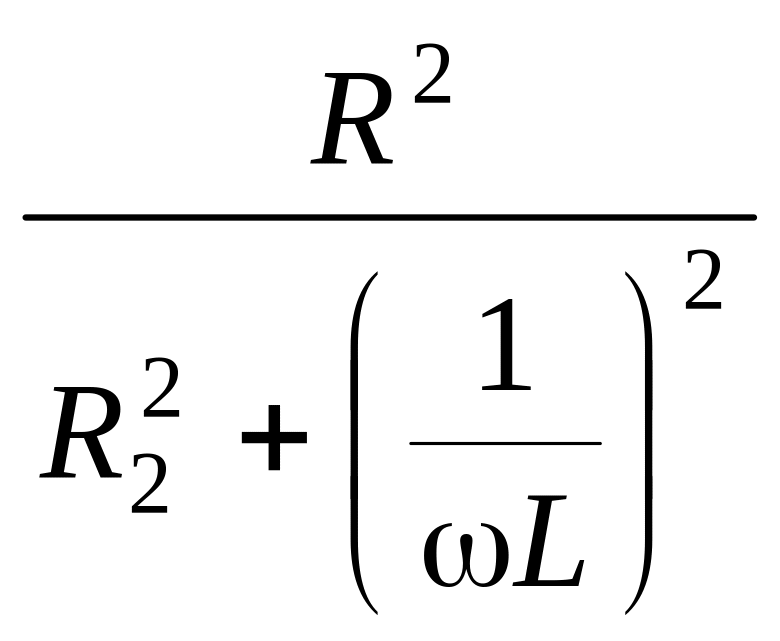= g₂ — активная проводимость второй ветви.

Таким образом, в цепи (рисунок 3.6) резонанс наступит при условии, что

= . (3.17)

Так как реактивные проводимости ветвей равны, то индуктивная составляющая тока I_L первой ветви будет равна емкостной составляющей тока I_C второй ветви, и они находятся в противофазе (рисунок 3.7), поэтому резонанс в рассматриваемой цепи носит название резонанса тока.

Рисунок 3.7 — Векторная диаграмма в режиме резонанса токов

При равенстве емкостной и индуктивной проводимости полная проводимость цепи будет равна сумме активных проводимостей ветвей:

.

Угол сдвига по фазе на входе цепи φ равен нулю. Согласно закону Ома , следовательно, в режиме резонанса токов ток на входе цепи зависит от суммарной активной проводимости ветвей , т.е. , в результате чего ток на входе цепи принимает минимальное значение. Токи в ветвях превышают ток на входе. Частоту, при которой может возникнуть резонанс токов, определим из условия резонанса (3.17):

= ;

избавимся от дроби:

;

раскрыв скобки, сгруппируем слагаемые с ω:

;

умножаем уравнение на :

.

Так как — волновое сопротивление, а — собственная частота последовательного колебательного контура, то окончательная формула для резонансной частоты параллельного контура примет вид:

ω_рез = ω₀ . (3.18)

Так как угловая частота выражается действительным числом, то из выражения (3.18) следует, что резонанс токов возможен в том случае, если R₁ > ρ и R₂ > ρ или R₁ < ρ и R₂ < ρ. Если R₁ = R₂, то резонансная частота не зависит от активного сопротивления: ω_рез = ω₀ Если же R₁ = R₂ = ρ =, то под знаком радикала имеет место неопределенность вида . Это случай так называемого безразличного резонанса. Резонанс токов наблюдается при любой частоте, так как эквивалентное сопротивление становится активным, не зависящим от частоты. В технике связи используются контуры хорошего и среднего качества, у которых R₁ и R₂ значительно меньше ρ. Для таких высокодобротных контуров, если пренебречь R₁ и R₂, резонансная частота ω_рез равна собственной частоте ω₀ последовательного колебательного контура.

Настроить параллельный колебательный контур в резонансе токов можно путем изменения параметров контура R₁, R₂, L, C или частоты напряжения источника.

При резонансе токов колебание больших энергий магнитного и электрического полей поддерживается при относительно малом токе в неразветвленной части цепи. Колебания происходят внутри колебательного контура без вовлечения (в идеальном случае) внешнего источника. Это очень важная особенность используется для компенсации угла сдвига по фазе.