2.9.5 Матричные уравнения контурных токов

Для получения контурных уравнений в матричной форме умножим слева обе части выражения закона Ома в матричной форме на матрицу контуров B:

. (2.38)

Согласно второму закону Кирхгофа в матричной форме

,

тогда

, (2.39)

или . (2.40)

Токи ветвей можно выразить через контурные токи, используя матрицу контуров и матрицу — столбец контурных токов, а именно (в матричной форме):

, (2.41)

где — транспонированная матрица контуров;

— матрица-столбец контурных токов.

Для подтверждения рассмотрим пример.

Для графа (рисунок 2.36) матрица контуров имеет вид:

.

Рисунок 2.36 — Граф электрической цепи

Матрица-столбец контурных токов:

.

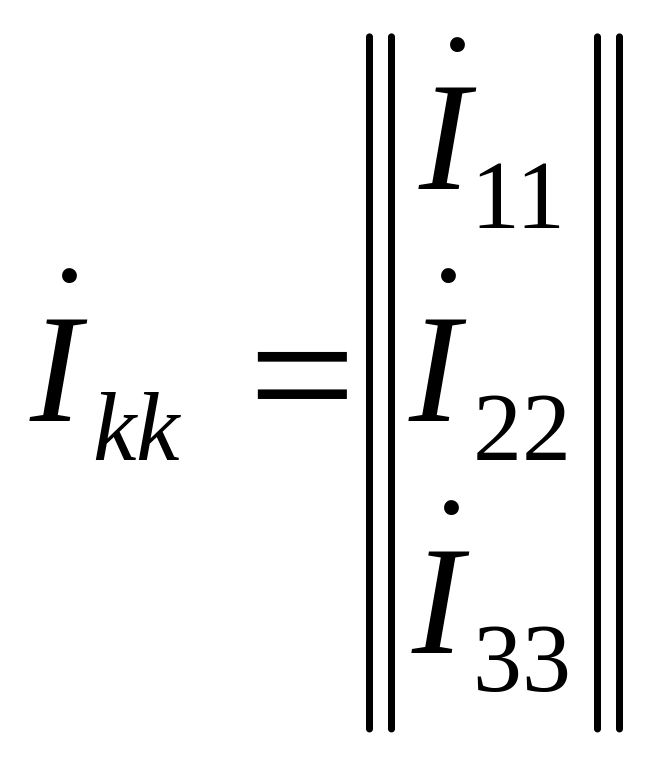Произведения двух матриц:

.

Таким образом, выражение (2.40) можно записать:

. (2.42)

Уравнение (2.42) представляет собой уравнения контурных токов в матричной форме.

2.9.6 Матричные уравнения узловых потенциалов

В тех случаях, когда число узлов меньше числа независимых контуров, целесообразно за искомые величины принять потенциалы узлов, положительный потенциал базисного узла равным нулю. За базисный можно принять любой из узлов.

Чтобы составить матричные уравнения узловых потенциалов, используем первый закон Кирхгофа в матричной форме:

.

Если умножить элементы узловой матрицы на потенциалы соответствующих узлов и затем просуммировать полученные произведения по столбцам, то можно видеть, что каждая такая сумма будет представлять собой напряжение ветви графа, равное разности потенциалов в узлах этой ветви. Эту систему уравнений можно записать в матричной форме:

, (2.43)

где — транспонированная узловая матрица;

— матрица-столбец потенциалов узлов.

Умножим слева левую и правую часть уравнения закона Ома в матричной форме: , — на узловую матрицу A и, учитывая, что и , в результате получим:

. (2.44)

Тройное матричное произведение

называют матрицей узловых проводимостей.

Здесь , , , — собственные проводимости узлов, представляющие собой сумму проводимостей всех ветвей, сходящихся к данному узлу;

— взаимная проводимость, представляющая собой проводимость ветви между узлами K и N, взятую со знаком «минус».

Если подставить в уравнение (2.44) значение первого матричного произведения Y_y и произвести умножение матриц в левой и правой частях, то можно записать полученный результат в виде системы алгебраических уравнений:

т.е. получена система уравнений, аналогичная системе, составленной по методу узловых потенциалов.

Найдя потенциалы узлов, определяют

,

а затем токи ветвей, пользуясь законом Ома.