2.5 Метод контурных токов

Сущность метода состоит в том, что за неизвестные принимают условные токи, которые как бы циркулируют в контурах схемы.

Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить по второму закону Кирхгофа, т.е. число неизвестных равно числу независимых контуров. Значит, метод контурных токов более экономичен (меньше уравнений в сравнении с методом уравнений Кирхгофа).

Для вывода основных уравнений метода рассмотрим схему цепи (рисунок 2.17).

В данной схеме два независимых контура, значит, полагаем, что в каждом независимом контуре течет свой контурный ток и . Задав их направления и направление обхода контуров (обычно по часовой стрелке), составим по второму закону Кирхгофа уравнения для независимых контуров, учитывая, что по смежной ветви (с сопротивлением ) течет сверху вниз ток и :

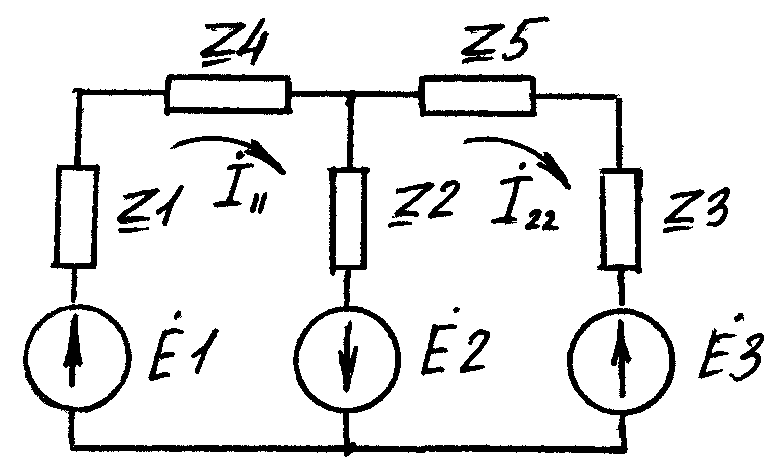
Рисунок 2.17 — Схема цепи для иллюстрации метода контурных токов

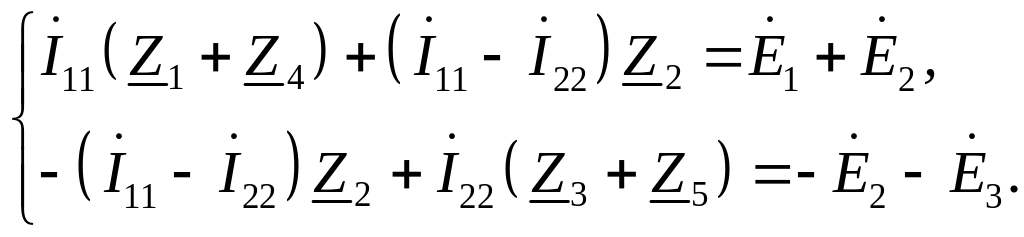(2.22)

Преобразуем систему уравнений (2.22), сгруппировав контурные токи

(2.23)

Если обозначим:

— сопротивление контура, по которому протекает контурный ток ;

— сопротивление контура, по которому протекает контурный ток ;

— сопротивление смежной ветви, взятое с отрицательным знаком;

— контурная ЭДС первого контура;

— контурная ЭДС второго контура,

то система уравнений (2.23) будет иметь вид:

. (2.24)

Если бы в схеме было больше двух контуров, например четыре, то система уравнений состояла бы из четырех уравнений:

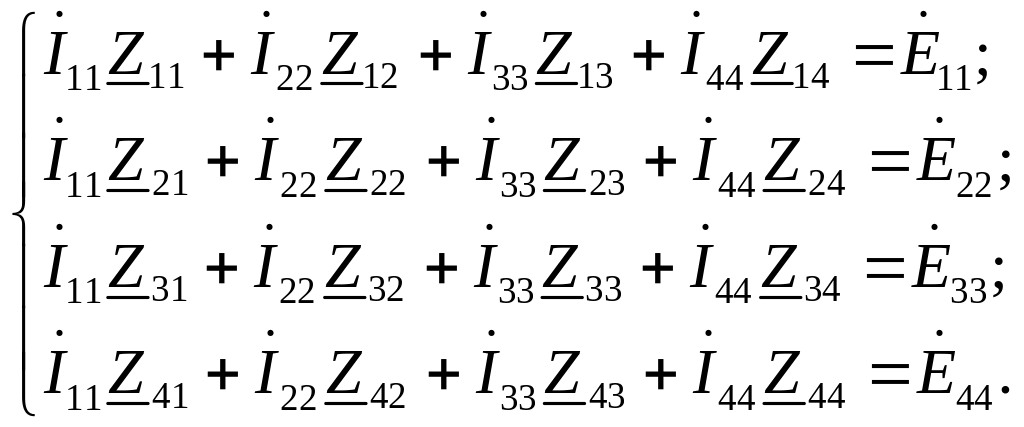(2.25)

Решение системы уравнений относительно искомых контурных токов может быть найдено с помощью определителей:

;

,

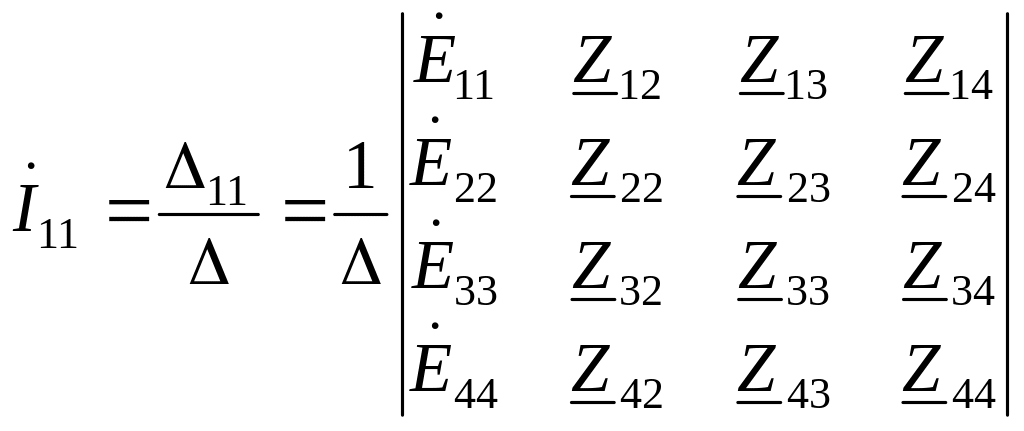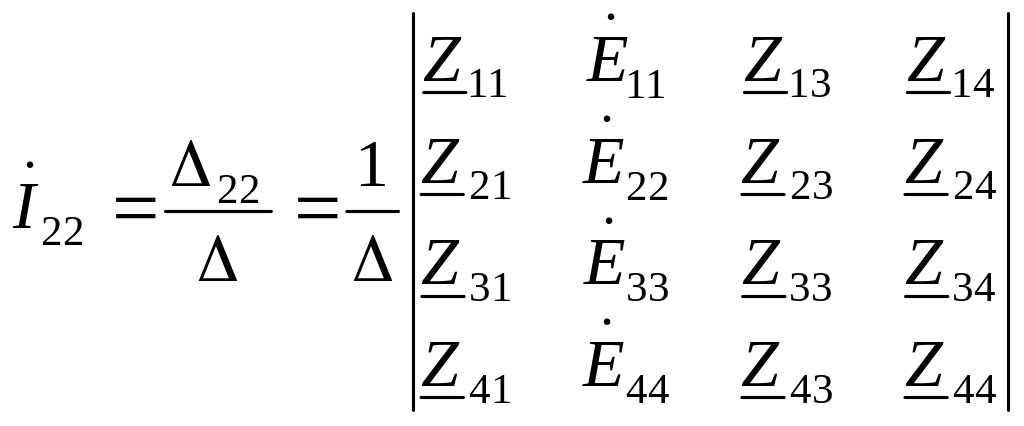и т.д., где главный определитель состоит из коэффициентов при неизвестных токах:

.

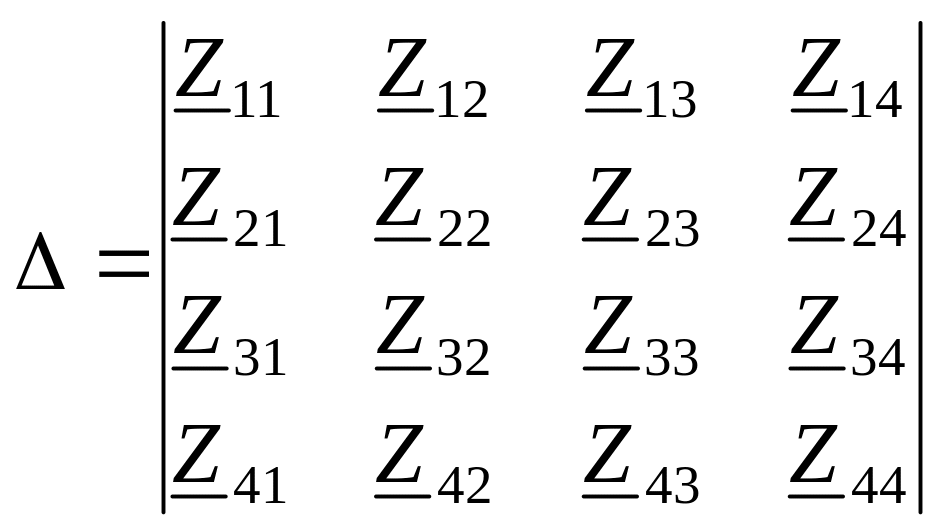Например, для системы уравнений (2.24)

; ,

где — главный определитель;

; — вспомогательные определители.

Общее решение системы и уравнений относительно тока:

, (2.26)

где — входное сопротивление k-го контура.

Расчет электрических цепей методом контурных токов ведут такой последовательности. Полагают, что в каждом независимом контуре протекает свой контурный ток. Задают их положительные направления, которые обозначают на схеме. Выбирают направления обхода контуров и по второму закону Кирхгофа составляют уравнения для независимых контуров. Решив полученную систему уравнений, находят контурные токи. Затем задают положительные направления действительных токов в ветвях и обозначают их на схеме. Значения токов в ветвях определяют алгебраической суммой соответствующих контурных токов, проходящих по данной ветви.

Если представить, что токи всех ветвей направлены к верхнему узлу (рисунок 2.10), то уравнения для их определения будут следующими:

; ; .

Пример. Используя условия задачи в п. 2.5, определить токи в ветвях методом контурных токов.

Решение. Воспользуемся методикой расчета, изложенной в п. 2.5, представим, что по ветвям двух независимых контуров циркулируют два контурных тока I₁₁, I₂₂, как показано на рисунке 2.18.

Рисунок 2.18 — Схема электрической цепи к примеру в п. 2.5

Задав направление обхода контуров по часовой стрелке, т.е. совпадающим с направлением контурных токов, составим систему уравнений по второму закону Кирхгофа в комплексной форме:

Подставив известные величины сопротивлений и ЭДС, имеем:

Решение полученной системы дает контурные токи:

А;

А.

Для нахождения действительных токов в ветвях зададим их положительные направления и обозначим их на схеме (см. рисунок 2.16). Тогда

А; А;

А; А;

А; А.

Таким образом, решение задачи двумя методами дало одинаковый результат.