Свойства дисперсии

1. Дисперсия постоянной равна 0.

Доказательство D[с]=0

D[с]=M[c²]-M²[c]=c²-c²=0

2. Постоянный множитель можно выносить за знак дисперсии, возводя ее в квадрат.

Доказательство:

D[cx]=c²D[x]

D[cx]-M[c²x²]-M²[cx]=c²M[x²]-c²M[x]=c²([M[x]²-M[x]])=c²D[x]

3. Дисперсия суммы независимых случайных величин

D[х+у]=D[х]+D[у]

D[х+у] = М[х+у]²-М²[х+у] = М[х²+2ху+у²]-(М[х]²+М[у]²)= М[х²]+М[2ху]+ М[у²]-М²[х]-М²[у] - М[2ху]= М[х²]-М²[х]+М[у²]-М²[у]=D[х]+ D[у].

Заметим, теорема обобщается на любое число взаимно независимых слагаемых. По определению следует, что дисперсия есть неотрицательное число и имеет квадратичную размерность.

Пример.

Найти дисперсию случайной величины , плотность распределения которой задана

;

;

Пример № 2.

Число очков, выбиваемых при одном выстреле из 2-х стрелков, подчиняется следующему распределению:

x1	1	2	3
Р	0,3	0,2	0,5

x2	1	2	3
Р	0,1	0,6	0,3

Найти дисперсию случайных величин x₁ и x₂.

M[x₁]=0,3+0,4+1,5=2,2;

M[x₂]=0,1+1,2+0,9=2,2;

D[x₁+x₂]=D[x₁]+D[x₂]=M[x₁²]-M²[x₁]+M[x₂²]-M²[x₁];

x12	1	11	9
Р	0,3	0,2	0,5

x22	1	4	9
Р	0,1	0,6	0,3

M[x₁²]=0,3+0,8+4,5=5,6;

M[x₂²]=0,1+2,4+2,7=5,2;

D[x₁+x₂]=5,6-4,84+5,2-4,84=10,8-9,68=1,12.

D[x₁]=0,76;

D[x₂]=0,36.

Роль математического ожидания и дисперсии на практике

Пример 1: Если нужно сравнить две марки стали по уровню ударной вязкости , что достаточно для каждой марки стали вычислить математическое ожидание ударной вязкости. Лучшей будет та марка стали, у которой математическое ожидание окажется выше

Пример 2: При одинаковом значении математического ожидания более качественным является стальной лист, имеющий минимальный разброс механических свойств. Тот лист лучше, у которого меньше значение дисперсии, т.е. меньше разброс механических свойств.

Среднее квадратическое отклонение

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относятся среднее квадратическое отклонение , определяемое по формуле:

Дисперсия квадрата совпадает с размерностью х- средним квадратическим отклонением.

Мода и медиана

Определение: Модой дискретной случайной величины называется ее наиболее вероятное значение.

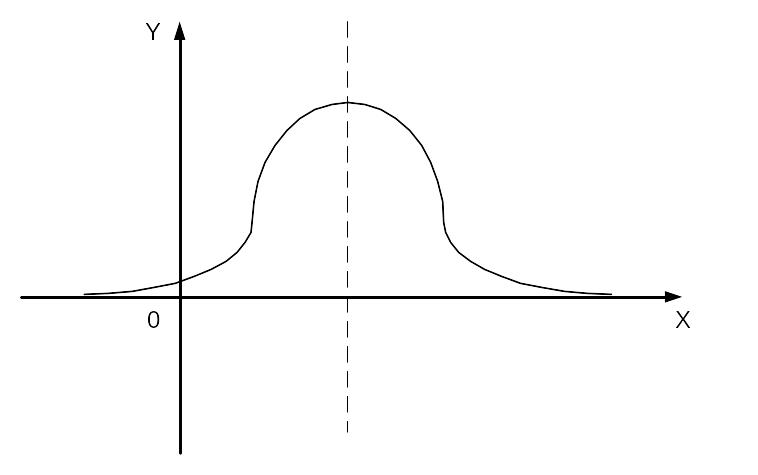
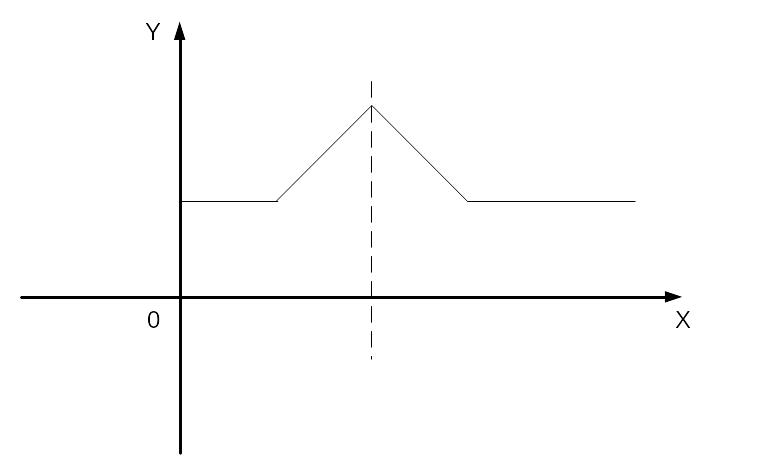
Геометрически мода является абсциссой в точке кривой распределения или полигона распределения. Ордината которой max-на. В общем случае мода и математическое ожидание не совпадают.

Модой непрерывной случайной величины называется то ее значение, при котором плотность распределения f(x) – максимальна. В частном случае, когда распределение является симметричным и имеет моду , и существует математическое ожидание; то оно совпадает с модой и с центром симметрии распределения.

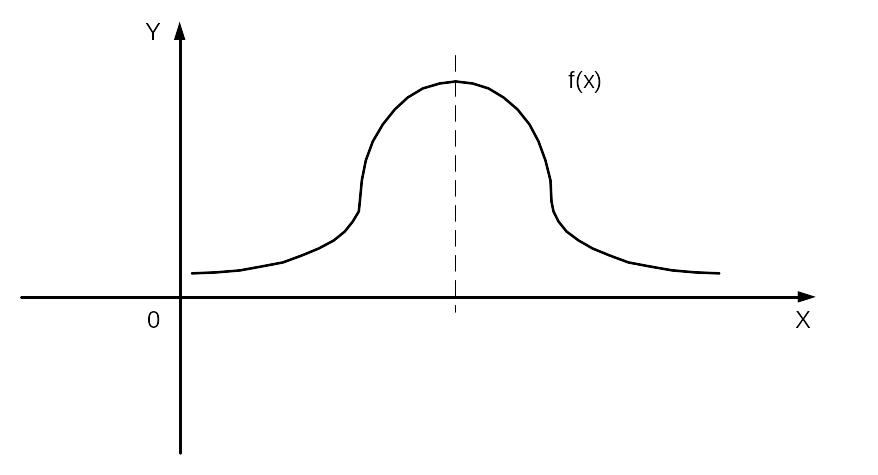
Медианой непрерывной случайной величины называется такое ее значение, для которого одинаково вероятно окажется ли случайная величина меньше либо больше медианы.

.

Геометрически медиана – абсцисса точки, в которой площадь ограниченной кривой распределения делится пополам. В случае симметричного распределения, имеющего моду, медиана совпадает с математическим ожиданием и модой.