Министерство образования Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Самарский государственный аэрокосмический университет имени академика С.П.Королева»

РАССЧЕТ И ИССЛЕДОВАНИЕ НЕРЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ

САМАРА 2004

Цель работы: ознакомление с методами расчета нерекур­сивных цифровых фильтров и способами их реализации с помощью ЭВМ; ис­следование различных методов синтеза НЦФ, их свойств и особенностей; приобретение практических навыков расчета НЦФ на ЭВМ.

1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

1.1. Особенности нерекурсивных цифровых фильтров

Нерекурсивные цифровые фильтры (НЦФ) во временной области опи­сываются разностным уравнением вида

(1)

где x(n) и y(n) - последовательность отсчетов входного и выход­ного сигналов соответственно, a a_i - константы-коэффициенты (передаточной функции) фильтра.

Как видно из уравнения (1), каждый отсчет выходного сигнала определяется взвешенной суммой отсчета входного сигнала в текущий момент времени x(n) и N-1 отсчетов входного сигнала в предшест­вующие моменты: x(n-1), x(n-2),..., x(n-N+1). Здесь и ниже, если не оговорено особо, будем принимать шаг временной дискретизации Т = 1 . Нетрудно видеть, что импульсная характеристика фильтра (отклик на единичный импульс) имеет конечную длительность и содержит N отсчетов, поэтому такие фильтры часто именуют фильтрами с конеч­ной импульсной характеристикой (КИХ- фильтры). Заметим, что НЦФ всег­да являются КИХ - фильтрами. Вместе с тем, КИХ - фильтры могут вы­полняться как по нерекурсивным, так и по рекурсивным схемам. Ясно, что значения отсчетов импульсной характеристики h(n) в моменты времени n=0,1,...,N-1 тождественно равна величинам коэффициентов уравнения (1):

(2)

Передаточная функция H(z) НЦФ определяется z преобразованием его импульсной характеристики:

(3)

Для получения комплексной частотной характеристики необходимо положить в выражение (3) z=e ^jw, тогда

H(e ^jw)= = (4)

Выражение (4) представим в показательной форме

(5)

где модуль составляет амплитудно-частотную характеристику (АЧХ) фильтра, а аргумент - фазочастотную характеристику (ФЧХ).

В нерекурсивной форме можно построить цифровые фильтры различных видов: частотно-избирательные, дифференциаторы, преобразователи Гильберта, а также обладающие специальными характеристиками, например, согласованные фильтры. В настоящей работе изучаются преимущественно частотно-избирательные фильтры.

Перечислим некоторые особенности КИХ-фильтров. К достоинствам таких фильтров можно отнести следующее:

• возможность получения строго линейной фазочастотной характе­ристики;

• абсолютная устойчивость при нерекурсивной реализации;

• возможность проще, чем в фильтрах с бесконечной импульсной характеристикой (БИХ), минимизировать шумы, возникающие в процессоре фильтра за счет выполнения арифметических операции с конечной точностью.

Вместе с тем, КИХ-фильтрам присущи и негативные качества. В частности, для получения высокой избирательности в полосно-пропускающих фильтрах требуются импульсные характеристики с большим числом отсче­тов N. При использовании в алгоритме фильтра прямой свертки (1) необходимо выполнить большой объем вычислений: N- операций умно­жения и N-1 -сложения на один отсчет выходного сигнала. Поэтому в КИХ-фильтрах для получения "хороших" амплитудных характеристик обычно требуются большие аппаратурные затраты, чем в БИХ-фильтрах. Заметим, что этот недостаток можно несколько ослабить, если использовать алго­ритм косвенной свертки на основе быстрого преобразования Фурье [1,3].

Целесообразно выделить два вида НЦФ: с линейной ФЧХ и минимально-фазовые. Характерным признаком фильтров второго вида является расположение нулей передаточной функции (3) в пределах круга единичного радиуса комплексной z -плоскости. Минимально-фазовые фильтры обладают xoрошим разрешением по времени: при равных условиях по избирательности такие фильтры имеют наиболее короткую импульсную характеристи­ку [2].

1.2. Нерекурсивные фильтры с линейной ФЧХ [I.2.3]

Для получения точно линейной ФЧХ в НЦФ с передаточной функцией (3) (частотной характеристикой (4)) на коэффициенты фильтра а_i или, что то же самое, на отсчеты импульсной характеристики h(n) накладывает­ся условие симметрии. Эта симметрия может быть четной и нечетной. При­меры симметричных импульсных характеристик приведены на рис.1. Как видно, здесь возможны 4 случая. Соответственно этому различают фильтры четырех видов:

N - нечетное, симметричные коэффициенты:

а_е = а _N-1-e , е=0,1,...,(N-3)/2 (рис.1.а);

N - четное, симметричные коэффициенты:

а_е = а _N-1-e , е=0,1,...,N/2-1 (рис.1,б);

N - нечетное, антисимметричные коэффициенты:

а_е = а _N-1-e , е=0,1,...,(N-3)/2; (рис.1.в);

a_(N-1)/2 =0

N - четное, антисимметричные коэффициенты:

а_е = - а _N-1-e , е=0,1,...,N/2-1 (pиc.1.г).

Учитывая перечисленные условия и воспользовавшись формулами Эйлера, можно преобразовать выражение (4) и получить частотные характеристики фильтров в форме:

вид1 H(e ^jw) =e^{-jLw ,} (6)

где L=(N-1)/2 ; C₀ =a_(N-1)/2; Cl =2a_(N-1)/2-l, ,l=1,...,N-1/2;

вид 2 H(e ^jw) = e ^-j(L+0,5)w , (7)

где L=N/2-1 ; C_l =2a_N/2-1-l; l =0,1,...,N/2-1;

вид 3 H(e ^jw) = e^-jLw (8)

где L=(N-1)/2 ; C₀ =2a_(N-1)/2-l; l =1,...,(N-1)/2 ;

вид 4 H(e ^jw) = e^{-j(L+0,5)w ,} ₍₉₎

где L=N/2-1 ; C_l =2a_N/2-1-l; l =0,...,N/2-1

Анализируя формулы (6) - (9), нетрудно убедиться в строгой ли­нейности фазочастотных характеристик фильтров. В самом деле, в ука­занных формулах выражения под знаком суммы являются вещественными и на фазу не влияют, выражения в показателях комплексной экспоненты, составляющие ФЧХ, являются линейными функциями частоты w.

h(n)

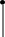
a

0 10 n

h(n)

б

0 9 n

h(n)

в

0 10 n

h(n)

г

0 9 n

Рис.1

1.3. Постановка задачи проектирования цифровых фильтров

Проектирование цифровых фильтров состоит из трех основных эта­пов:

определение требуемых характеристик фильтра;

аппроксимация этих характеристик на основе использования физи­чески реализуемых дискретных систем;

реализация фильтра при использовании арифметики с ограниченной точностью;

Требуемые (желательные) характеристики фильтра определяются из условия его использования по назначению. Применительно к частотно-из­бирательному фильтру на первом этапе определяются требования к АЧХ фильтра (значения граничных частот полосы пропускания и полосы непропускания, затухание в полосе заграждения, допустимая неравномерность АЧХ) и требования к ФЧХ (с линейной фазой или минимально-фазовый).

Для описания желательных частотных характеристик D(w) может использоваться весьма широкий набор средств. В то же время частотная характеристика физически реализуемого нерекурсивного фильтра, как следует из формул (4),(6),(7),(8),(9), представляется тригонометрическим многочленом конечной длины. Возникает задача аппроксимации требуемой (целевой) функции тригонометрическим рядом. Задача аппроксимации, как уже отмечалось, решается на втором этапе проектирования, и ее целью является расчет коэффициентов передаточной функции цифровых фильтров (ЦФ). Этот этап включает в себя следующие шаги:

выбор критерия аппроксимации, т.е. уточнение смысла приближенного равенства

H(e ^jw) D(w) (10)

на заданном интервале частот w;

оценку необходимого порядка фильтра N;

расчет коэффициентов передаточной функции ai, при которых выполняется условие (10) в смысле выбранного критерия;

проверку выполнения заданных требований к характеристикам фильтра. Если требования выполняются, то можно перейти к следующему этапу. В противном случае следует увеличить порядок фильтра и выполнить последующие шаги второго этапа повторно.

На третьем этапе производится расчет разрядности регистров процессора, с помощью которого предполагается реализовать фильтр. Содержание этого этапа зависит от выбранной элементной базы и в настоящей работе не рассматривается.

Ко второму этапу проектирования, который часто именуют также синтезом ЦФ, возможен различный подход. Наиболее эффективными являются методы, в которых оптимизируется вся совокупность коэффициентов фильтра из условия минимума ошибки аппроксимации. В частности, практическое применение находят

метод наименьших квадратов

мин, (11)

в котором минимизируется взвешенный квадрат ошибки аппроксимации [2] Здесь g(w) ~ весовая функция, позволяющая управлять точностью anпроксимации на различных участках частотного интервала (w₁, w₂);

метод наилучшей равномерной (чебышевской) аппроксимации [1,2]

макс g(w)/H(e ^iw) – D(w)/ мин. (12)

w₁ w w₂

Суть чебышевского метода состоит в минимизации взвешенного модуля мак­симальной ошибки аппроксимации. Процедуры (11),(12) предполагают опти­мизацию всех коэффициентов фильтра. В этой случае синтезируются опти­мальные фильтры. Смысл такой оптимальности состоит в том, что не су­ществует другого фильтра порядка, меньшего N, обеспечивающего мень­шую ошибку аппроксимации в соответствии с выбранным критерием.

Помимо этого находят применение методы синтеза фильтра, в кото­рых оптимизируются значения части коэффициентов передаточной функции фильтра. Для поиска наилучшего решения в таких случаях обычно исполь­зуются методы линейного программирования. Эти методы, естественно, не приводят к оптимальным фильтрам. Более того, существуют методы синте­за НЦФ, в которых не проводится оптимизация, а по некоторому правилу желательной физически нереализуемой частотной характеристике ставит­ся в соответствие частотная характеристика физически реализуемого фильтра.

Различные методы синтеза фильтров отличаются по сложности и ис­пользуются в зависимости от характера решаемой задачи.

1.4. Синтез НЦФ методом взвешивания, (методом временного "окна")

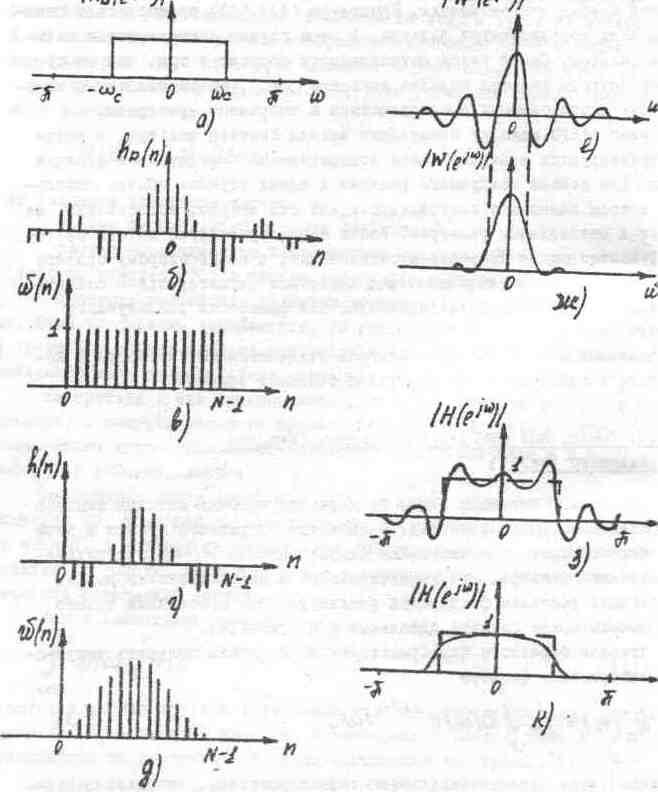
Метод "окна" является одним из наиболее простых методов синтеза нерекурсивных цифровых фильтров. В качестве отправного пункта в этом методе берется требуемая частотная характеристика D(w) синтезируе­мого цифрового фильтра. Эта характеристика и не обязательно должна удовлетворять условиям физической реализуемости. Простейшим такого рода примером может служить идеальный ФНЧ (рис.2,а).

/H₀(e ^jw)/ /W(e ^jw)/

Рис.2

С помощью обратного преобразования Фурье можно получить импульс­ную характеристику фильтра

h_D(n)= (13)

Полученная таким образом импульсная характеристика, как правило, опре­делена на интервале (- , ). т.е. бесконечна по длительности, и имеет ветвь в области отрицательного времени п < О. Пример такой характеристики приведен на рис. 2.б., на котором показана импульсная характеристика идеального цифрового ФНЧ. Ясно, что такого вида им­пульсная характеристика не удовлетворяет условию физической реализуемости, так как имеет ветвь в области отрицательного времени. Кроме того, бесконечная импульсная характеристика не соответствует КИХ-структуре синтезируемого фильтра.

Исключить отмеченные затруднения можно путем усечения импульсной характеристики и сдвига усеченной характеристики в область положитель­ного времени. Заметим, что такой временной сдвиг не влияет на АЧХ фильтра, а вносит лишь соответствующее запаздывание по фазе. В обоб­щенном смысле усечение можно рассматривать как умножение импульсной характеристики на временное окно. Временное окно w(n) - это после­довательность отсчетов конечной длительности n =0,1,..., N-1. Существуют окна с различными формами огибающей. Простейшим временным окном является окно прямоугольной формы (рис.2,в). Ясно, что примене­ние прямоугольного окна эквивалентно простому усечению. Полученная таким образом импульсная характеристика h(n)=h_D(n) w(n) показа­на на рис. 2,г. Нетрудно видеть, что эта характеристика соответствует казуальному (физически реализуемому) цифровому КИХ-фильтру.

На практике используют обычно окна не прямоугольные, а специаль­ной формы. В настоящее время разработано большое количество окон, удовлетворяющих различным требованиям. Их общей отличительной особенностью является плавное нарастание амплитуды отсчетов последовательности ок­на и также плавное спадание в конце (рис.2,д.). Операцию умножения импульсной характеристики на окно часто называют взвешиванием, а само окно - весовой последовательностью. С этим связано название метода ~ "метод взвешивания".

Операция взвешивания приводит к тому, что частотная характерис­тика синтезированного фильтра оказывается отличной от исходной тре­буемой характеристики. Формально это явление можно объяснить очень просто. Взвешивание изменяет импульсную характеристику. Так как час­тотная и импульсная характеристики связаны между собой преобразованием Фурье, то изменяется и частотная характеристика. Однако для определе­ния сути этого изменения целесообразно рассмотреть влияние операции взвешивания в частотной области. Из теории преобразования Фурье из­вестно, что умножению двух временных функций (импульсной характерис­тики и окна) в частотной области соответствует свертка их спектров (в нашем случае исходной частотной характеристики и спектра окна)[1,3]. Спектр прямоугольного окна имеет вид функции Sin x/x (рис. 2,е), в то время как типичное окно непрямоугольной формы имеет спектр без явно выраженных боковых лепестков (рис. 2,ж). Как можно видеть, свертка исходной частотной характеристики с функцией вида Sin x/x приведет к возникновению пульсаций в результирующей частотной характеристике. В теории сигналов это явление называют эффектом Гиббса. Суть эффекта Гиббса состоит в возникновении колебаний огибающей АЧФ в окрестности резкого изменения этой характеристики (рис. 2,з).

Пульсации АЧХ, обусловленные эффектом Гиббса, приводят к ухудшению избирательности фильтров. Частотные характеристики фильтров при использовании прямоугольного окна в большинства приложений оказываются неудовлетворительными.

Спектры окон специальной формы имеют малый уровень боковых лепестков. Влияние таких окон на требуемые обычно "идеальные" частотные характеристики состоит в сглаживании разрыва характеристики в пределах некоторой переходной полосы конечной ширины. Суть такого сглаживания применительно к идеальному ФНЧ показана на рис. 2, к.. Как видно в результате этого сглаживания устраняются лепестки в АЧХ (за счет некоторого расширения главного лепестка характеристики). Частотная характеристика (спектр) окна должна обладать возможно узким главным лепестком, малыми боковыми лепестками. Во временной области окно должно описываться достаточно простыми функциями.

Эти требования являются противоречивыми. Разработано большое число различных окон, в разной степени удовлетворяющих перечисленным требованиям. Не останавливаясь на особенностях, приведем описание некоторых из окон:

функция Хэмминга

w(n) = 0,54 + 0,46 cos( ), n =- _,...,

функция Блэкмана

w(n) = 0,42 + 0,5 cos( )+0,08 cos( ) ;

n =-(N-1/2,...,(N-1)/2;

функция Ланшоца

w(n)=[sin / ]⁴,n=- _{,..., ;}

где L – целое;

Функция Кайзера

w(n)= ,

n =- _{,..., .}

Здесь I₀( x) - модифицированная функция Бесселя первого ряда нулевого порядка, - положительное число, параметр окна.

Метод окон применим для синтеза широкого класса НЦФ. В этом одно из его достоинств. Другим достоинством является простота самого метода и машинной программы, с помощью которой он реализуется (см. ниже). Так как в методе окна не производится оптимизация параметров фильтров, то оказывается затруднительным предсказать точное значение параметров фильтра (например, полосы пропускания или заграждения), ко­торые получатся в результате синтеза. Поэтому может потребоваться кор­ректировка параметров фильтра, которая выполняется путем повторного расчета методом проб и ошибок. При использовании ЭВМ этот недостаток метода окна не является существенным.

1.5. Синтез нерекурсивных фильтров на основе частотной выборки

Напомним, что задача синтеза нерекурсивного ЦФ состоит в опреде­лении коэффициентов а_i передаточной функции Н(z) , (см.формулу(З)) физически реализуемого фильтра, частотные характеристики которого удовлетворяют заданным требованиям. Ниже нам удобнее будет вести речь не о коэффициентах, а об отсчетах импульсной характеристики синтези­руемого ЦФ, которые связаны со значениями коэффициентов соотношени­ем (2). К задаче синтеза КИХ-фильтра на основе частотной выборки возможен следующий подход. На частотной шкале в равноотстоящих точках берутся выборочные значения Н(к), k=0,..., N-1 требуемой частотной характеристики. Пример взятия такой частотной выборки для идеального ФНЧ показан на рис.3,а. Потребуем, чтобы значения частотной xapaктеристики синтезируемого фильтра на выбранных часто­тах совпадали с выборкой Н(к). Однако на всех промежу­точных частотах ; не будем сначала накладывать каких-либо ограничений на соответствие реальной и идеальной частотных характеристик. Тогда для импульсной харак­теристики достаточно выполнить операция обратного дискретного преобразования Фурье (ДПФ) над частотной получения искомой выборкой: (14)

0 0,5 f 0 0,5 f

а ) б)

«Свободные»

отсчеты

1 2 3

0 0,5 f 0 0,5 f

в) г)

Заметим, что на рис. 3,а взяты амплитуды , в то время как в формуле (14) фигурируют комплексные величины . Поэтому в частотной выборке необходимо учитывать также фазочастотную характеристику. Ниже на этом вопросе остановимся подробнее. Ясно, что качество синтезируемого фильтра определяется значениями частотной характеристики на всех частотах , а не только на выборочных частотах .

Прямая процедура (14) синтеза не представляет возможности пред­сказать поведение частотной характеристики между частотными выборками. Более того, фильтры, синтезируемые в соответствии с этой про­цедурой, в большинстве приложений оказываются неудовлетворительными, вследствие недопустимо больших пульсаций частотной характеристики. Для примера на рис. 3.б показана АЧХ цифрового ФНЧ, соответствующая частотной выборке, приведенной на рис 5.а.

Для уменьшения пульсаций используется метод, в котором наряду с полосами пропускания и непропускания выбирается переходная полоса конечной ширины (рис.З.в). В полосах пропускания и непропускания, как и ранее, задается частотная выборка. Однако в переходной полосе отсчеты частотной характеристики на выборочных частотах полагаются неопределенными, "свободными". Значения этих элементов частотной выборки подбираются таким образом, чтобы расхождение в полосах пропус­кания и (или) непропускания частотной характеристики синтезируемого фильтра и требуемой характеристики было минимальным (рис.3.г). Для этого используются итерационные алгоритмы оптимизации, хорошо реали­зующиеся на ЭВМ.

Составим выражение для интерполирующей частотной характеристики и сформулируем условия синтеза фильтров с линейной фазой и действительной импульсной характеристикой, которые должны выполняться. Для этого подставим выражение (14) в формулу (3) и, переменив порядок суммирования, запишем

(15)

Просуммируем внутреннюю сумму в выражении (15) (геометрическую прогрессию) и представим последнее в виде

(16)

Положим в (16) и после элементарных преобразовании для частотной характеристики получим

(17)

При выводе выражения (17) не накладывалось каких-либо ограничений на характеристики синтезируемого фильтра.

Рассмотрим ограничения, которые следует наложить на частотные выборки, чтобы получить действительную импульсную характеристику и точную характеристику с линейной фазой. Из теории преобразования известно, что фильтры с действительной импульсной характеристикой интервале частот должны иметь частотные выборки симметричными по амплитуде и иметь антисимметричную фазу. Однако, учитывая свойства линейных дискретных систем, удобнее выразить условия симметрии на интервале (0.2 π), а не на интервале . Тогда, если частотные выборки записаны в виде , то условия cимметрии при нечетном N можно записать в виде

Подставив выражение (18) в формулу (17), после элементарных преобразовании [1, с.85-86] получим (опуская множитель с линейной фазой)

(19)

При четном N условия симметрии можно записать в виде

(20)

Условие для выборки k=N/2 обусловлено тем, что, как следует из выражения (7), фильтр с линейной фазой при четном N должен иметь при .

Используя выражения (17) и (20), для соответствующей частотной характеристики можно получить

(19.а)

Формулы (19), (19.a) являются удобными выражениями для использования при синтезе фильтров методом частотной выборки. Задача синтеза реша­ется итерационным методом на ЭВМ на основе алгоритмов линейного программирования. Подход к этой задаче состоит в следующем.

Частотные характеристики(19), ( 19,а) можно представить в виде

. (21)

Выражение (22) можно рассматривать кал взвешенную сумму интерполирующих функций . Сравнив выражение (21) с (19) и (19.а), нетрудно убедиться в том, что множество функций не зависит от конкретных параметров (кроме заданной величины порядка N синтезируемого фильтра. Поэтому, приняв за основу множество функций можно построить процедуру синтеза НЦФ произвольного вида из класса фильтров с линейной ФЧХ. В такой процедуре оптимизация АЧХ осуществляется путем варьирования свободными частотными выборками. Итерационная процедура оптимизации частотной характеристики предпола­гает минимизацию максимального значения взвешенной ошибки

где ω изменяется в областях 1 и 3 (см.рис.3,в), - желае­мая частотная характеристика, - произвольная весовая функция, позволяющая устанавливать различные ошибки на разных интервалах аппрок­симации. На начальном этапе итерационной процедуры изменяемые выбор­ки в выражении (21) выбираются произвольно.

Отметим, что для получения коэффициентов передаточной функции синтезируемого фильтра (равных согласно (2) отсчетам импульсной характеристики) необходимо выполнить операции обратного ДПФ (14) над частотной выборкой Н(К), в которой учитываются также оптимизированные переменные члены.

Метод частотных выборок можно применять для синтеза цифровых

фильтров нижних и верхних частот (ФНЧ, ФВЧ), полосно-пропускающих; полосно-заградительных фильтров, дифференциа-торов и преобразовать Гильберта. Этот метод наиболее эффективен при синтезе узкополосных фильтров, поскольку в этом случае большая часть частотных выборок равна нулю.

1.6. Метод наилучшей равномерной (чебышевской) аппроксимации

Теория метода чебышевской аппроксимации достаточно сложна, поэтому в данных методических указаниях мы ограничимся сведениями, позволяющими составить лишь общее представление об этом методе. Обратимся сначала к обобщенной теореме Чебышева.

Пусть заданы функции:

(22)

-линейная комбинация N косинусов;

- непрерывная на интервале частот ;

- кусочно-непрерывная на этом интервале весовая функция.

Ставится задача аппроксимации целевой функции тригонометрическим рядом (22) с весом . Ошибку такой аппроксимации можно записать в виде

(23)

Теорема Чебышева утверждает, что ошибка равномерного приближения в функции частоты имеет колебательный (пульсирующий) характер, и существует признак, присущий наилучшей равномерной аппроксимации. В соответствии с этим признаком для выделения наилучшего приближения необходимо и достаточно, чтобы ошибка принимала равные друг другу по абсолютной величине и противоположные по знаку экстремальные значения в N+1 последовательно расположенных точках частотного интервала . Иначе ошибка имеет пульсирующий характер, амплитуды пульсаций при наилучшем равномерном приб­лижении должны быть одинаковыми. Этому условию соответствует одна единственно возможная совокупность значений коэффициентов в функции (22). При любых других значениях коэффициентов приближение не будет наилучшим и признак не выполняется.

Аналитически обобщенную теорему Чебышева можно записать в виде

(24)

Последнее отношение истинно при любом значении частоты, принад­лежащем интервалу . Заметим, что частоты, на которых ошибка принимает экстремальные значения, называют точками альтернанса, а рассматриваемую теорему - теоремой о чебышевском альтернансе.

Теорема Чебышева справедлива и для случая, когда аппроксимируе­мая функция задана не на всем интервале частот , а только на отдельных подынтервалах, не имеющих общих точек. В этом случае функ­ция должна быть доопределена на промежуточных подынтервалах так, чтобы получилась непрерывная функция на замкнутом интервале, включающем все заданные подынтервалы. Все точки альтернанса должны располагаться только на заданных подынтервалах. Это обстоятельство весьма сущест­венно при проектировании частотно-избирательных фильтров, когда предъ­являются требования к точности аппроксимации характеристик только в полосах пропускания и непропускания, разделенных переходной по­лосой. В качестве примера на рис. 4 приведены

заданная (целевая) (ЦФ) и аппроксимирующая (АФ) функции для фильтра ниж­них частот при N=6.

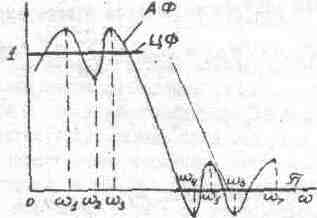
Рисунок 4.

Не выясненными остались два вопроса: возможность использования метода при проектировании различных физически реализуемых фильтров; способ определения аппроксимирующей функции.

Обратимся к первому из них. Передаточные функции физически реа­лизуемых фильтров не всегда описываются выражением (22). Для того что­бы избежать возникающие в связи с этим затруднения запишем для пере­даточной функции фильтра:

(25)

где P(w) - некоторая подходящая непрерывная функция. Тогда для ошибки аппроксимации можно записать:

(26)

где и

Таким образом, для фильтров, передаточные функции которых пред­ставлены в виде (25), задача аппроксимации сводится к описанной выше классической постановке (23).

Покажем возможность представления передаточных функций физически реализуемых НЦФ в виде уравнения (25) на конкретных примерах. Обратим­ся к фильтрам с линейной фазой. Опуская в выражении (6) член с линей­ной фазой (так можно поступить, так как в выражениях (23) и (26) рассматривается модуль ошибки аппроксимации), нетрудно видеть, что эта передаточная функция непосредственно выражается в виде линейной комбинации косинусов и в этом случае . Рассмотрим далее (8). Линейную комбинацию синусов в этом выражении можно записать в виде

(27)

где

в этом случае, очевидно, . Такого рода примеры можно продолжить.

Обратимся к задаче определения функции наилучшего равномерного приближения. Предложено несколько способов решения этой задачи. Наиболее практичен метод, для которого созданы эффективные ма­шинные программы, основанные на итерационной процедуре, известной под названием второго алгоритма Ремеза [1]. Напомним, что функция определяется N своими коэффициентами . Таким образом, задача состоит в отыскании оптимального вектора коэффи­циентов/С/.

Предположим, что порядок фильтра N выбран. Заметим, что для оценки порядка фильтра существует приближенная эмпирическая формула [2, с. 12.1] (см. также п.2.4). Основа алгоритма Ремеза состоит в следую­щем. Теорема о чебышевском альтернансе (24) утверждает, что в случае оптимального решения ошибка имеет по крайней мере N+1 экстремумов. Предположим вначале, что множество частот экстремумов известно. Тогда на каждой из этих частот модуль ошибки (26) составит некоторую (неизвестную) величину δ. Учитывая знакопеременный ха­рактер ошибки, можно составить систему N+1 уравнений:

(28)

В этой системе неизвестными являются N коэффициентов ряда (22) и ошибка δ. Система уравнений (28) может быть решена и таким об­разом определены искомые коэффициенты. Однако вследствие исходной не­определенности множество частот может не соответствовать точкам альтернанса, поэтому поиск оптимального решения проводится итерацион­ный способом. Каждый цикл этих итераций выполняется в два шага [1,2].

Шаг I. Выбирают N+1 значений , решают систему уравне­ний (28), вычисляют в результате этого коэффициенты Сk и δ. Таким образом получают тригонометрический полином по косинусам, кото­рый в точках отличается от целевой функции на величину .

Шаг 2. Анализируют ошибку на всем интервале частот . Для этого ошибка рассчитывается с малым шагом по частоте (на плотной частотной сетке). Если ошибка во всей области аппроксима­ции, то полученное выше решение является оптимальным. Если найдутся частоты, на которых , то выбирают новое множество экстремаль­ных частот путем рассмотрения N+1 точек, в которых ошибка максималь­ная и имеет чередующийся знак. Далее описанная процедура повторяется. Начальное множество частот можно взять произвольным. Можно пока­зать, что в этой процедуре δ на каждом шаге возрастает и в конце концов сходится к своей верхней границе.

Отметим, что в алгоритме Ремеза предложен способ вычислений, позволяющий избежать необходимость решения на каждом шаге системы урав­нений (28). Тем самым повышается эффективность алгоритма [2].

2. Особенности практического использования машинных методов проектирования нцф

2.1. Предварительные замечания

В инженерной практике при расчете частотно-избирательных НЦФ наиболее часто задаются требования к избирательности фильтра и точ­ности аппроксимации целевой функции : ширина переходной полосы F и максимально допустимые отклонения δ₁ АЧХ от номинального значения в полосе пропускания и (или) δ₂ в полосе задерживания. Необходимо найти минимальное число N (порядок фильтра) и вычислить коэффициенты передаточной функции. Однако рассмотренные выше методы проектирования ЦФ не вполне соответствуют такой постановке задачи. Во всех этих методах задача синтеза (расчета коэффициентов переда­точной функции) фильтра ведется в предположении, что порядок фильт­ра (число N ) известен и задан. В методах с оптимизацией (частот­ная выборка, равномерная чебышевская аппроксимация) при заданных пе­реходной полосе и порядке фильтра минимизируются максимальные ошибки аппроксимации. Выбор порядка фильтра N для такого расчета произ­водится на основе эмпирических формул, графиков, таблиц, построенных по экспериментальным данным, а также на основе опыта и интуиции раз­работчика. Разумеется, такая предварительная оценка порядка N не может быть точной, поэтому часто приходится использовать метод проб и ошибок и производить расчет фильтра многократно, последовательно приближаясь к оптимальному решению. При использовании ЭВМ итерацион­ные процедуры последовательных приближений оказываются вполне прием­лемыми для практического использования. Рассмотрим основные особен­ности соответствующих алгоритмов и программ.

2.2. Метод окна

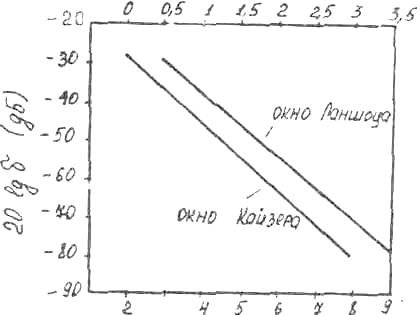
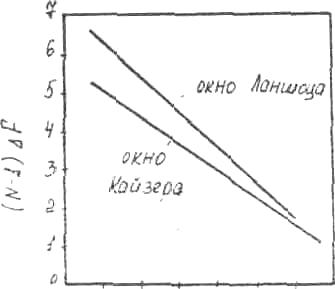
Неравномерность АЧХ-фильтра, полученного с помощью этого мето­да, зависит от амплитуды боковых лепестков выбранной функции окна, и, когда окно выбрано, эти амплитуды, очевидно, фиксированы. Для выбоpa параметра функции окна можно воспользоваться графиками (рис.5), на которых показана зависимость максимального уровня пульсаций АЧХ в полосе пропускания и в полосе задерживания (δ₁= δ₂=δ) для окон Ланшоца и Кайзера (см. п.1.4) от параметров этих функций.

Ширина переходной полосы F АЧХ-фильтра зависит от ширины основ­ного лепестка амплитуд­ного спектра окна, кото­рая, в свою очередь, опре­деляется величиной N .Когда выбран вид исполь­зуемой функции окна и подобрана величина ее параметра, два других параметpa N и F могут свободно варьироваться. Эти параметры связаны соотно­шением неопределенности вида.

Окно Кайзера Параметр окна

Рис. 5

N F =С, (29)

где С- константа, зависящая от вида используемого окна и его параметра.

Для выбора N можно воспользоваться графиками (рис.6), на которых показана зависимость произведения (N-1) F от максимального уровня пульсаций δ (δ₁ =δ₂ =δ).

Рассмотрим пример выбора исходных данных для синтеза НЦФ методом окна.

Предположим, что требуется синтезировать ФНЧ, полоса пропускания которого составляет 0...0,08, полоса заграждения 0,16...0,5. Уровень боковых лепестков-40 дБ относительно 1. Отметим, что здесь используется шкала нормированных частот 0...0,5. Возьмем окно Кайзера. По графикам на рис.5 выберем параметр окна Кайзера, соответствующего заданному уровню боковых лепестков. Получим параметр окна =3,5.

-90 -80 -70 -60 -50 -40 -30 -20

20 lg (дб)

Рис. 6

Как видно из исходных дан­ных, переходная полоса фильтра составляет 0,16-0,08=0,08. Определим порядок фильтра N . Из графиков на рис.6 следует, что для уровня пульсации -40 дБ (N –1) F=2, таким образом, получим N = +1 26.

2.3. Метод частотной выборки

В этом методе, как уже отмечалось, частотная характе­ристика фильтра в полосах про­пускания и задерживания задает­ся своими выборочными значениями, взятыми в точках дискретизации час­тоты. Ширина переходной полосы определяется количеством выборочных значений, варьируемых в процессе синтеза фильтра. Совокупное число точек дискретизации частоты на интервале (0,1) нормированной часто­ты составляет N и определяется порядком синтезируемого фильтра. Таким образом, процедуре оптимизации АЧХ-фильтра должен предшествовать выбор порядка фильтра. Оценка порядка фильтра в этом методе про­изводится на основе экспериментальных данных. Однако, прежде чем об­ратиться к возможному способу такого выбора, рассмотрим в общих чер­тах подход к оптимизации АЧХ-фильтра, используемый в программе для ЭВМ. Оптимизация (подбор амплитуд выборок в переходной полосе) произ­водится методами линейного математического программирования. Такие алгоритмы имеют разнообразное применение.

Современные ЭВМ имеют развитое математическое обеспечение. В библиотеке научных программ алгоритмического языка Фортран ЕС ЭВМ имеется стандартная программа с именем АРММ, в которой запрограмми­рован алгоритм оптимизации. Суть такой оптимизации состоит в минимизации максимальной ошибки в полосе задерживания фильтра. Амплитуды пульсаций в полосе задерживания зависят от числа варьируемых выборок. Заметим, что амплитуды указанных пульсаций АЧХ характеризуют коэффи­циент передачи фильтра в полосе заграждения. Нетрудно видеть, что величина этих амплитуд, выраженная в децибелах относительно уровня передачи в полосе пропускания составляет затухание, вносимое в поло­су заграждения. Эмпирические данные уровня пульсаций в децибелах от­носительно уровня передачи в полосе пропускания, относящиеся к циф­ровому ФНЧ, приведены в табл.1 [I]. Сразу заметим, что к этим данным необходимо относиться с осторожностью, так как в случаях, когда син­тезируемый фильтр имеет "очень узкую" или "очень широкую" полосу про­пускания, затухание в полосе задерживания может выходить за указанные в таблице пределы.

Теперь рассмотрим способ оценки порядка фильтра N. Предположим, что заданы ширины полос пропускания, задерживания к переходной полосы, а также уровень пульсации δ₂ в полосе задерживания. Тогда, воспользовавшись данными табл. 1, можно определить число варьируемых выборок N_v , попадающих в переходную полосу шириной F. Далее нетрудно определить общее число выборок N, приходящихся на поло­су частот (0,1):

N =1/ FN_v (30)

Таблица 1

Число варьируемых выборок	Ожидаемый уровень максимальной ошибки в полосе задерживания находится в пределах, дБ
1 2 3	44...54 65...75 85...75

Рассмотрим пример. Предположим, полоса пропускания ФНЧ занимает интервал частот 0 ... 0,08, переходная полоса 0,08 ... 0,16 ( F=0,08) и полоса задерживания 0,16 ... 0,5. Пусть уровень ошибки 60 дБ. Для этого случая из табл. I получим N _v = 2.

Теперь по формуле (30) по­лучим искомую оценку порядка фильтра

N=1/0,08 х 2=25.

В практической работе следует иметь в виду, что программа АРММ чувствительна к точности вычислений. В используемой в данной работе программе реализуются вычисления с однократной точностью. При росте числа переменных Nv и соответствующем уменьшении уровня пульса­ций в полосе задерживания может потребоваться двойная точность вы­числений.

2.4. Минимаксный метод равномерной _чебышевской аппроксимации

Оптимальный в смысле критерия минимума взвешенной максимальной ошибки (23) метод синтеза КИХ-фильтров реализуется с помощью программы для ЭВМ с использованием алгоритма Ремеза [l.2]. Программа об­ладает большими возможностями: ее можно использовать для синтеза сложных, в том числе многополосных частотно-избирательных фильтров, диф­ференциаторов, преобразователей Гильберта. Вместе с тем, эта прог­рамма является наиболее сложной из всех рассматриваемых в настоящей работе программ, требует наибольшего машинного времени на выполне­ние.

Особенностью метода является возможность фиксации границ пере­ходных полос фильтра. Здесь, как и ранее, порядок фильтра N необ­ходимо задавать заранее. Однако в данном случае поиск фильтра наименьшего порядка, удовлетворяющего поставленным требованиям, с по­мощью итерационной процедуры последовательного приближения может оказаться малоэффективной процедурой, поскольку программа, несмотря на эффективность алгоритма, обладает малым быстродействием. Для уменьшения объема вычислений на ЭВМ, можно ориентировочно определить N _мин по следующей эмпирической формуле, справедливой для ФHЧ [l,2]:

N _мин=D₁ (δ₁, δ₂)/ F+ D₂ (δ₁, δ₂)/ F+1, (31)

Где D₁ (δ₁, δ₂)=[ 5,309 10^-3(lg δ₁)²+7,114 10^-2lg δ₁-4,761 10^-1]lg δ₂+[-2,66 10^-3(lg δ₁)²-5,91 10^-1lg δ₁-4,278 10^-1];

D₂ (δ₁, δ₂)=11,01217+0,51244(lg δ₁-lgδ₂),

δ₁, δ₂ - амплитуды пульсаций АЧХ в полосах пропускания и задержи­вания соответственно, F- нормированная ширина переходной поло­сы.

Используя формулу (30), можно, по крайней мере, найти начальную точку в упомянутой выше итерационной процедуре. В качестве примера возьмем ФНЧ с переходной полосой F= 0,08. Примем, что допусти­мые пульсации в полосах пропускания и заграждения δ₁= δ₂=δ = 0,1% (-60 дБ), при этом lgδ₁=lgδ₂=-3. Вычисления по формуле (31) дают результат N мин =24.

При практическом использования программы для синтеза многополос­ных фильтров (с числом полос > 2.) отмечены случаи возникновения больших аномальных ошибок (выбросов АЧХ) в переходных полосах фильт­ров. В результате моделирования процедуры синтеза фильтров получены некоторые способы для выбора входных параметров алгоритма, при кото­рых аномальные ошибки исключаются. Эти способы подробно изложены в литературе [I].

3. СОДЕРЖАНИЕ РАБОТЫ

Исследование рассмотренных выше методов синтеза НЦФ, их свойств и особенностей проводится путем анализа результатов расчета фильт­ров на ЭВМ. В этом исследовании в качестве отправного момента зада­ются тип фильтров, некоторая целевая функция (требуемая "идеальная" частотная характеристика), требования к точности аппроксимации це­левой функции. Применительно к частотно-избирательному фильтру могут задаваться полосы пропускания и непропускания, минимальное затуха­ние в полосе непропускания, допустимая неравномерность АЧХ (уровень пульсаций) и другие требования. На основании всех этих требований по методике, изложенной в разд. 2. (см.также разд.4), выбираются ис­ходные данные для машинного расчета ЦФ. Источником информации для последующего анализа служит распечатка результатов расчетов, которая выдается студентам. Перечислим кратко содержимое распечатки.

При расчете методом взвешивания на печать выводятся АЧХ фильт­ра без взвешивания (т.е. при прямоугольной форме временного окна), АЧФ со взвешиванием, импульсные характеристики для обоих этих слу­чаев, а также весовая функции - временное окно.

В случае использования метода равномерной чебьшевской аппрокси­мации на печать выводятся импульсная характеристика, частоты чебышевского альтернанса, расчетное затихание в полосе непрозрачности (абсо­лютное и в децибелах), амплитудно-частотная характеристика.

При расчете фильтров методом частотной выборки на печать выво­дятся значения оптимизируемых элементов выборки и вся частотная вы­борка, АЧХ фильтра для случаев, когда используется процедура оптими­зации и без оптимизации. Отметим, что здесь в случае без оптимизации АЧХ, варьируемые выборочные отсчеты полагаются равными нулю, т.е. эти отсчеты причисляются к полосе непропускания фильтра. Применительно к ФНЧ частотной выборке с оптимизацией АЧХ соответствует рис.3,в, а выборке без оптимизации - рис.3,a.

Помимо табличных данных с помощью печатающего устройства строят­ся все перечисленные выше амплитудно-частотные характеристики.

В работе студентам для изучения может быть предложен ряд вопро­сов.

I. Изучение особенностей методов синтеза фильтров.

Метод взвешивания. Особенности этого метода обусловлены харак­тером влияния временного окна на АЧХ фильтра, поэтому при анализе результатов расчета фильтра этим методом следует:

определить по АЧХ параметры синтезированного фильтра: полосу пропускания, полосу задерживания, неравномерность АЧХ в полосе про­пускания, затухание (абсолютное и в дБ) в полосе задерживания, сте­пень соответствия параметров заданным; рассмотреть временное окно и импульсные характеристики фильтра со взвешиванием и без взвешивания, определить характер их различия; определить, обладает ли фильтр линейной АЧХ.

Метод наилучшей равномерной чебышевской аппроксимации. Здесь также следует по АЧХ определить параметры фильтра, соответствие фак­тических параметров заданным; проверить выполнение теоремы о чебышевском альтернансе.

Метод частотной выборки. Для этого метода также следует опреде­лить по АЧХ параметры фильтра и сопоставить их с заданными значения­ми; сравнить АЧХ с оптимизацией и без оптимизации, дать объяснение их paзличию. В настоящем анализе, помимо табличных данных, следует рассмотреть графики АЧХ, дать объяснение виду полученных кривых.