Классификация сигналов

Различают детерминированные (его значение в любой момент времени можно определить точно) и случайные сигналы (случайная величина с некоторой вероятностью)

Следующий важный класс сигналов – сигналы с интегрируемым квадратом или сигналы с ограниченной энергией.

Еще один признак классификации сигналов, существенно влияющий на методы их анализа, - периодичность. Для периодического сигнала при любом t, (n – произвольное число, T – период). Любой периодический сигнал имеет бесконечную энергию.

Следующий класс – сигналы конечной длительности (финитные сигналы). Они отличны от нуля, но только на ограниченном промежутке времени.

Перейдем к более узким, так называемым тестовым сигналам, применяющимся для анализа сигналов и систем:

1. гармонические колебания 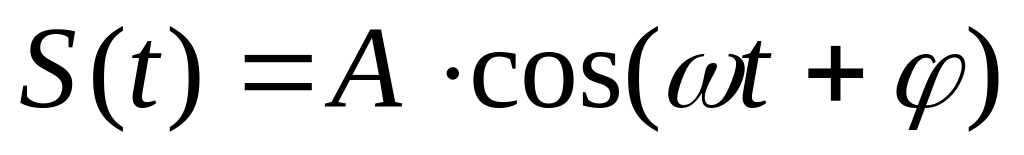, А – амплитуда, ω – частота, φ – начальная фаза. Применяется для анализа характеристик цепей.

Есть еще 2 важные в радиотехнике функции, тоже относящиеся к тестовым:

2. дельта-функция, или функция Дирака - бесконечный узкий импульс с бесконечной амплитудой, расположенной при «нулевом» значении аргумента функции.

S_{импульса} =1, . Сигнал невозможно реализовать физически. важен для теоретического анализа сигналов и систем. На графиках изображается жирной стрелкой, высота которой пропорциональна множителю, стоящему перед дельта-функцией. Одно из важных свойств – фильтрующее свойство: если присутствует под интегралом в качестве множителя, то результат интегрирования будет равен значению остального подынтегрального выражения в той точке, где сосредочен дельта-импульс.

3) функция единичного скачка , или функция Хевисайда, или функция включения. Она равна нулю для отрицательных значений аргумента и равна для положительных. При нуле функцию считают либо неопределенной, либо равной ½. Эту функцию удобно использовать при создании математических выражений для сигналов конечной длительности. (С помощью можно любую кусочно-заданную зависимость записать в виде единого математического выражения).

Основной целью анализа сигналов является сравнение сигналов друг с другом для выявления их сходства и различия. Можно выделить 3 основных составляющих анализа сигналов:

- измерение числовых параметров сигналов; к ним относятся энергия, средняя мощность и среднеквадратичное значение;

- разложение сигнала на элементарные составляющие; такое разложение производится с использованием ряда Фурье и преобразования Фурье;

- количественное измерение степени «похожести» различных сигналов(корреляционный анализ).

Энергетические характеристики сигналов

Одной из составляющих анализа сигналов является измерение их количественных параметров: 1) энергии; 2) средней мощности (за заданный промежуток времени) 3) мгновенной мощности.

Их определения, принятые в теории сигналов, отличаются от обычных.

Обычные «физические» понятия мощности и энергии: если к резистору с сопротивлением R приложено напряжение U, то мощность равна ; энергия за время T.

Пусть к этому резистору приложен сигнал S(t). Мощность, рассеивающаяся в резисторе, будет зависеть от времени t, т.е. речь идет о мгновенной мощности:

.

Чтобы вычислить выделяющуюся за t энергию, p(t) нужно проинтегрировать:

Среднюю мощность за заданный промежуток времени t получим, разделив энергию на длительность временного интервала:

Энергия и мощность интересуют нас с точки зрения сравнения различных сигналов. Поэтому исключим сопротивление нагрузки( R = 1). И тогда получим формулы для энергии, мгновенной мощности и средней мощности, принятые в теории сигналов:

Мощность имеет размерность В², а энергия – В²с.