Предел функции.
Пределом
функции
в точке
называется такое число
,
что для любой последовательности
значений аргумента
,
сходящейся к числу
,
последовательность
,
соответствующих значений функции
стремится к этому числу
и обозначается:
.
При нахождении
пределов функций нужно использовать
следующие свойства предела функции:
если существуют конечные пределы
и
,
то
1)
;
2)
;
3)
;
4)
(или
),
если
(или 0);
5)
,
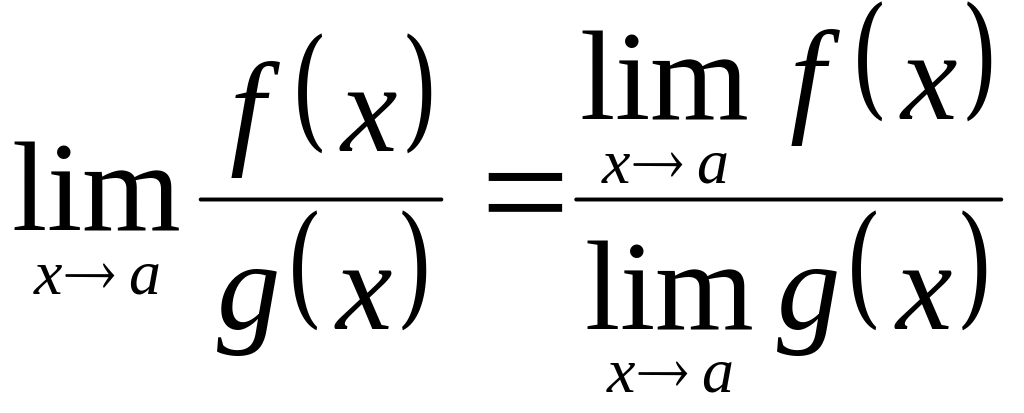если
.
Пример.
Вычислить
.
Решение: Разделим
числитель и знаменатель на
,
получим:
.
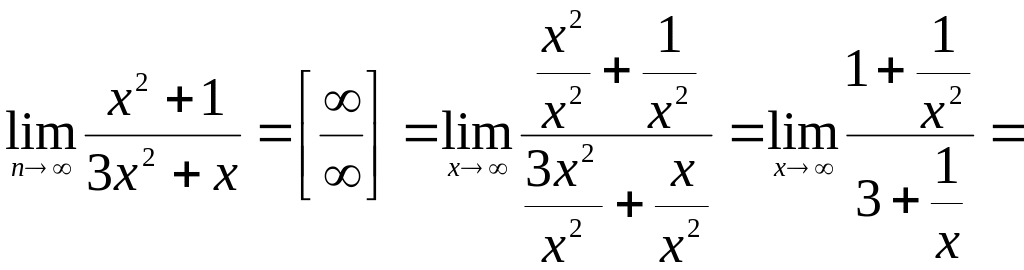
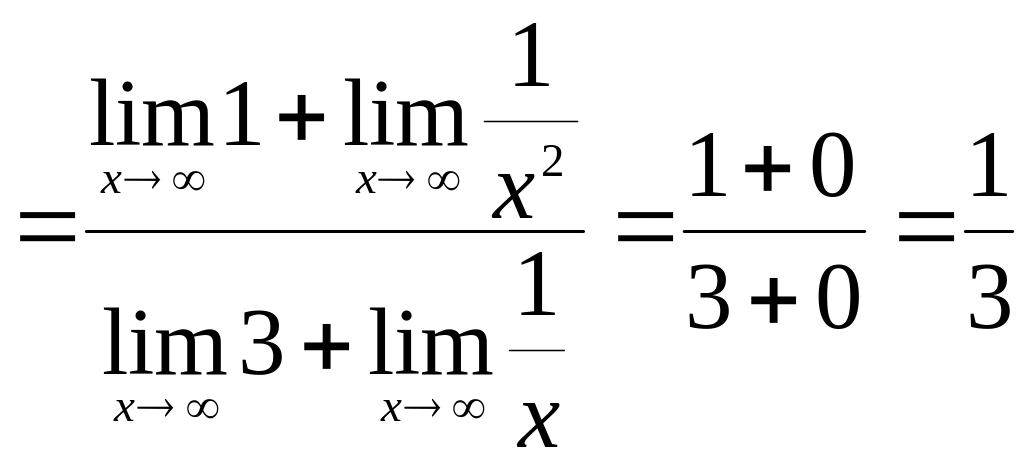При нахождении
пределов функций также полезно знать
первый
замечательный предел:
и следствия из него:
;
;
;
и второй
замечательный предел:
.
Пример. Вычислить
предел
.
Решение.
.
Пример. Вычислить
предел
.
Решение.
.
Общий метод (правило
Лопиталя) вычисления пределов в случаях
неопределенности
и
рассматривается в дифференциальном
исчислении.
Пусть
функция от
,
имеющая пределом число
,
когда
стремится к числу
.
Предположим, что все значения величины
меньше, чем число
,
то есть
.
Символически это выражается очень
удобной записью:
(вместо
).
Тогда предел
называют пределом функции
в точке
слева или левосторонним
пределом.
Аналогично,
при
,
то есть
предел
называют пределом функции
в точке
справа или правосторонним
пределом.
Левосторонний и правосторонний пределы функции в точке называются односторонними пределами.
Дадим определение непрерывности функции в точке.
Функция называется непрерывной в точке , если:
1) функция определена в точке и в некоторой ее окрестности, содержащей эту точку ;
2)
функция
имеет одинаковые односторонние пределы
в этой точке
,
то есть
;
3) эти односторонние
пределы должны быть равны значению
функции
в этой точке
:
.
Функция
называется разрывной
в
точке
,
если она определена в сколь угодно малой
окрестности точки
,
но в самой точке
не удовлетворяет хотя бы одному из
условий непрерывности.
Точки разрыва функции можно разделить на два типа.
Точка разрыва функции называется точкой разрыва 1-го рода, если существуют конечные односторонние пределы функции в этой точке, которые не равны между собой или равны между собой, но не равны значению функции в этой точке. Если хотя бы один из односторонних пределов функции в точке не существует или равен бесконечности, то – точка разрыва функции 2-го рода.
Пример.
Исследовать
на непрерывность функцию и построить
ее график
.
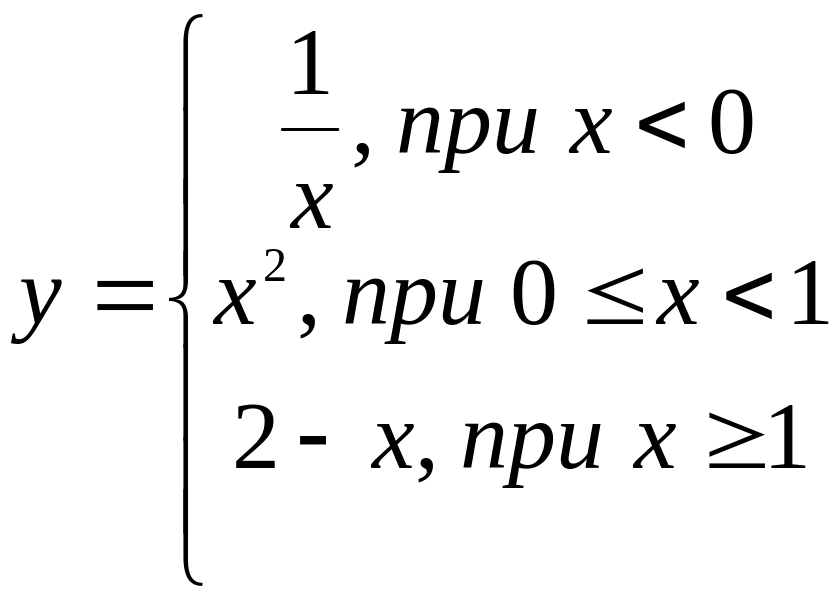Решение.
Областью
определения данной функции
является вся числовая ось, то есть
.
Точками «подозрительными» на точки
разрыва являются точки
и
,
так как при переходе через эти точки
функция
меняет свое аналитическое выражение с
дробно – рациональной на квадратичную
и с квадратичной на линейную, соответственно.
Исследуем непрерывность функции в точке :
Поскольку условие непрерывности функции в точке нарушается, то – точка разрыва функции , т.к. левосторонний предел функции в точке равен бесконечности, то – точка разрыва 2-го рода.
Исследуем непрерывность функции в точке :
Условие непрерывности функции в точке выполняется, значит, функция в точке непрерывна.
Построим график функции :
