Основные элементарные функции

Следующие шесть типов функции называются основными элементарными функциями:

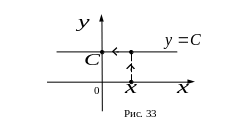
I. Постоянная функция – функция, ставящая в соответствие каждому действительному числу одно и то же число . (См. рис. 33) , .

II. Степенная функция .

а) – целое число.

Если – четное, то , .

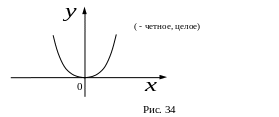
Если – нечетное, то , .

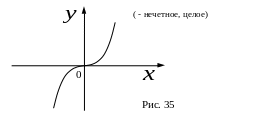
Графики функции ( – целое) показаны на рис. 36 и рис. 37 соответственно.

В случае если – четное, – множество всех действительных чисел, кроме нуля, .

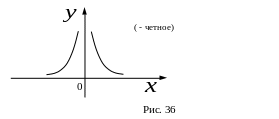
В случае если – нечетное, , .

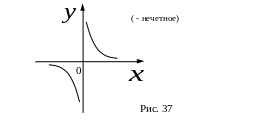
б) – рациональное, то есть , , ;

.

Пример графика функции или . (См. рис. 38). , .

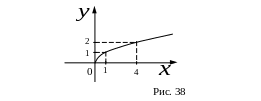
Пример графика функции или .(См. рис.39).

, .

III. Показательная функция

, , .

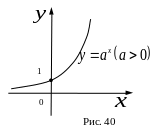
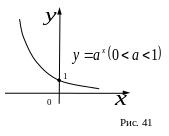
IV. Логарифмическая функция

, ,

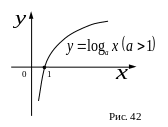
V. Тригонометрические функции

а) , , .

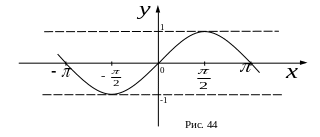
б) , , .

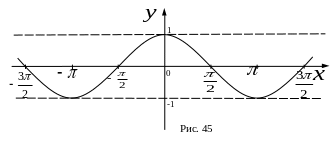
в) , – множество всех действительных чисел , за исключением точек , , .

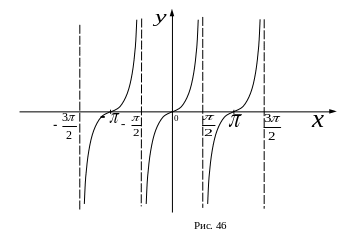
г) , , .

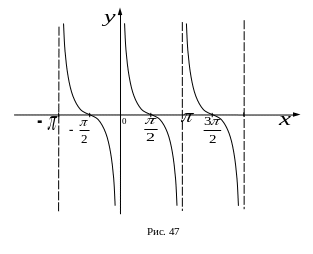
IV. Обратные тригонометрические функции

а) , , .

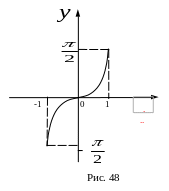
б) , , .

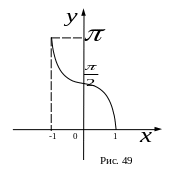
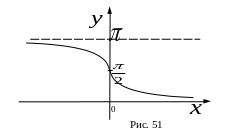
в) , ,

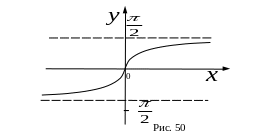
г) , ,

Предел числовой последовательности

Функция , заданная на множестве всех натуральных чисел называется числовой последовательностью и обозначается , где элемент соответствует номеру . Будем задавать числовую последовательность формулой своего общего члена .

Пример. – числовая последовательность , так как – формула общего члена последовательности.

При : .

При : .

При : и т.д.

Пределом числовой последовательности называется конечное действительное число , если для любого сколь угодно малого числа существует такое натуральное число , что для всех членов последовательности с номерами выполняется неравенство . В краткой записи это выглядит так:

и обозначается: .

Определим – окрестность точки как множество всех , удовлетворяющих условию: , что эквивалентно двойному неравенству: .

Тогда понятие предела геометрически означает, что какую бы малую – окрестность точки не взяли, найдется такой номер , начиная с которого все последующие члены последовательности будут находиться в этой окрестности (См. рис. 52).

Последовательность, имеющая конечный предел, называется сходящейся или стремящейся к этому пределу, а неимеющая конечного предела – расходящейся. «Стремление» последовательности к своему пределу будем обозначать как .

Пример. Доказать по определению, что .

Решение. Возьмем любое сколь угодно малое . Имеем: , когда или . Значит существует такой номер , равный целой части числа , то есть такое целое число , что , то есть , начиная с которого все последующие члены с номерами , , , , ... будут находиться в – окрестности точки , то есть в интервале . (См. рис.53). При , при .

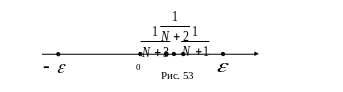
Замечание.

означает, что , ;

означает, что , .

При вычислении пределов числовой последовательности полезно использовать следующие их свойства, если существуют конечные пределы и , то

1) , ;

2) , ;

3) ;

4) ;

5) 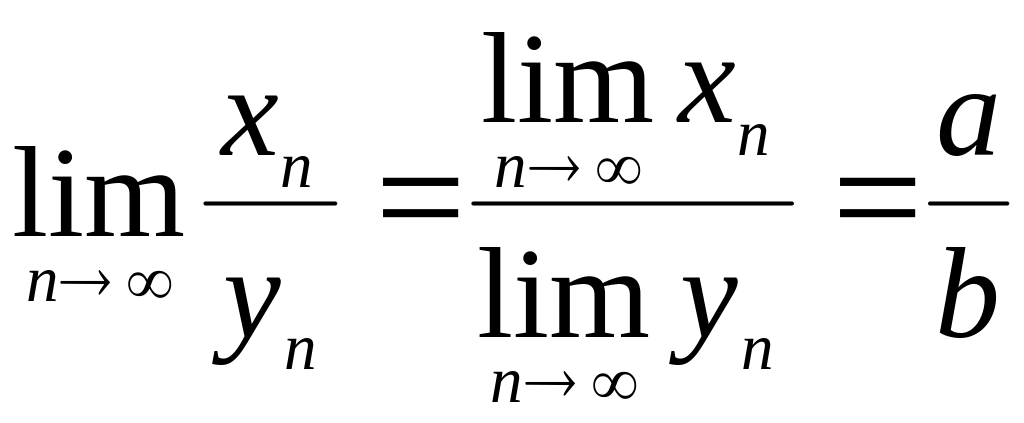, если ;

6) , если .

Пусть требуется найти предел отношения двух последовательностей, сходящихся к бесконечности, то есть и .

Непосредственно применить свойство о пределе частного двух последовательностей нельзя. Предварительно необходимо преобразовать выражение к виду, допускающему применение указанных свойств. В связи с этим выражение называется неопределенностью, а его преобразование к виду, позволяющему найти предел – раскрытие неопределенности.

Заметим, что выражение , когда последовательности в числителе и знаменателе стремятся к нулю, также называются неопределенностью.

Пример. Вычислить .

Решение. Разделим числитель и знаменатель на – наибольшую из степеней в числителе и знаменателе:

.
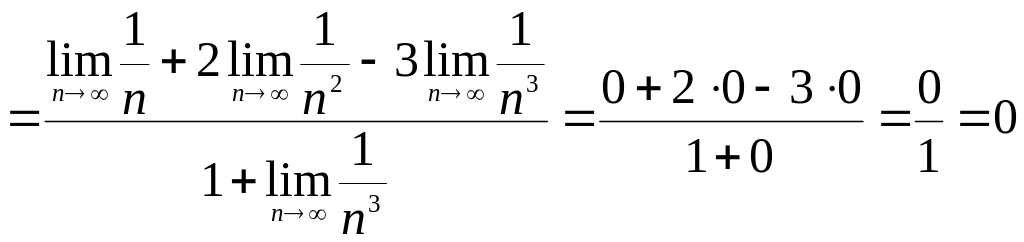