Векторное произведение векторов
Три некомпланарных (непараллельных одной плоскости) вектора , и , взятые в указанном порядке, образуют правую тройку векторов, если из конца третьего вектора поворот от первого вектора ко второму вектору по кротчайшему пути виден против хода часовой стрелки, и левую, если по часовой. (См. рис. 8)
Векторным произведением вектора на вектор называется такой вектор , что:
1)
,
;
2)
;
3) тройка векторов
,
,
и
– правая, и обозначается
.
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами , , и :
,
,
.
Поскольку тройки
векторов
,
и
левые, то
,
,
.
Свойства векторного произведения:
1)
;
2)
;
3)
,
;
4)
.
Векторное произведение двух векторов и находится по формуле:
.
Пример. Найти
векторное произведение векторов
и
.
Решение.
.
Ответ:
.
Геометрический смысл векторного произведения состоит в том, что площадь параллелограмма, построенного на векторах и (см. рис. 9) равна модулю векторного произведения векторов и , так как:
Следовательно, площадь треугольника, построенного на векторах и (см. рис. 10) равна половине модуля векторного произведения, построенного на векторах и , то есть
.
Пример. Найти
площадь треугольника, построенного на
векторах
и
.
Решение.
и
.
Тогда
;
,
следовательно
(кв.
ед.).
Ответ:
кв. ед.
Смешанное произведение векторов
Рассмотрим
произведение трех векторов
,
и
,
составленное следующим образом:
,
то есть первые два вектора
и
умножаются векторно, а их результат
скалярно на третий вектор
.
Такое произведение векторов называется
векторно-скалярным
или смешанным
и обозначается
,
то есть
.
Смешанное произведение трех векторов , и представляет собой число, равное объему параллелепипеда, построенного на этих векторах (см. рис. 11), взятое со знаком «плюс», если эти три вектора образуют правую тройку и со знаком «минус», если они образуют левую тройку векторов.
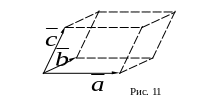
Свойства смешанного произведения:
1)
;
2)
;
3)
;
,
;
4) Если
,
то векторы
,
и
компланарны.
Смешанное
произведение трех векторов
,
и
заданных
своими координатами,
то есть
,
,
вычисляется по формуле:
.
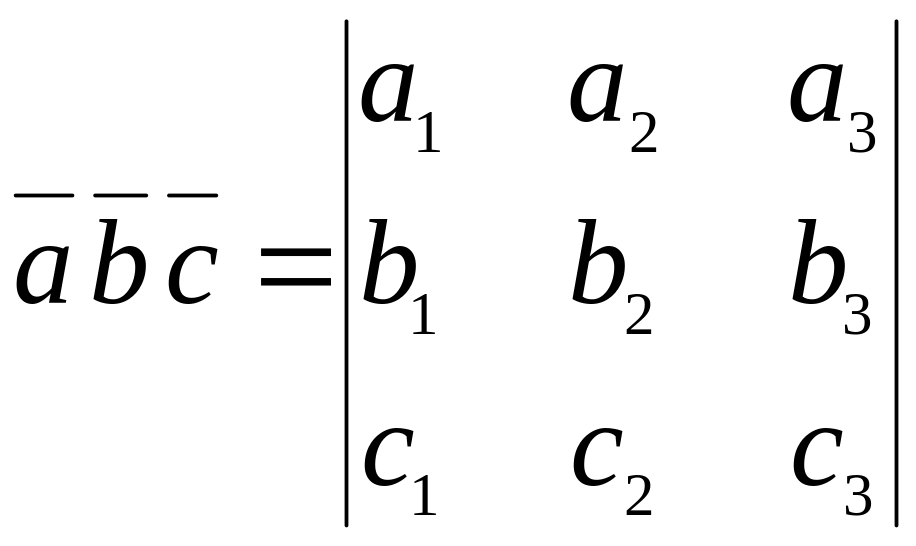Пример. Вычислить
смешанное произведение векторов
,
,
.
Решение.
,
,
.
Тогда
.
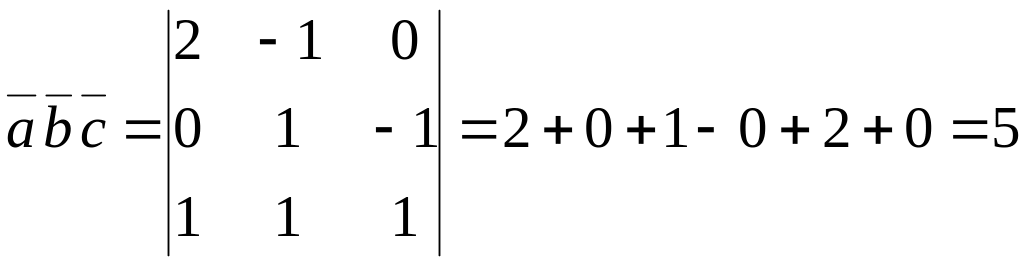Ответ:
.
Исходя из геометрического смысла смешанного произведения, имеем, что объем параллелепипеда, построенного на векторах , и (см. рис. 11) вычисляется по формуле:
.
Объем треугольной пирамиды, построенной на трех векторах , и (см. рис. 12) вычисляется по формуле:
.
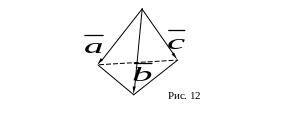
Пример.
Найти объем пирамиды, построенной на
векторах
,
и
.
Решение.
.
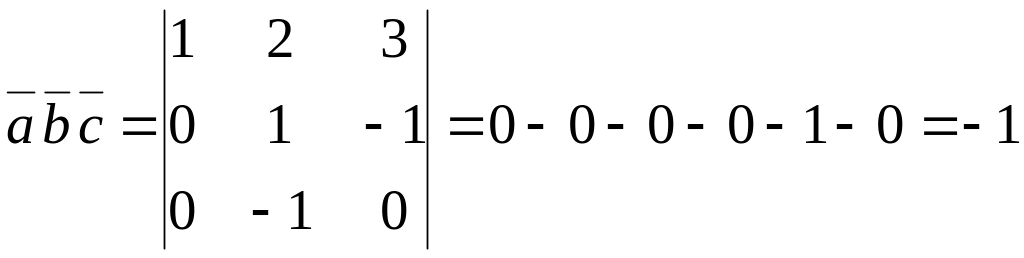Тогда
(куб. ед.).
Ответ:
(куб. ед.).
§ 3. Прямая на плоскости
Под прямой понимают прямую линию. Введение на плоскости прямоугольной декартовой системы координат позволяет определять положение точки на плоскости заданием двух чисел – ее координат, а положение прямой на плоскости определять с помощью уравнения, то есть равенства, связывающего координаты точек прямой.
Уравнение прямой
позволяет изучение геометрических
свойств прямой заменить исследованием
ее уравнения. Так, для того, чтобы
установить лежит ли точка
на
прямой
,
достаточно проверить (не прибегая к
геометрическим построениям) удовлетворяют
ли координаты точки
уравнению
этой прямой, то есть выполняется ли
равенство
.
Пример. Лежит
ли точка
на прямой
.
Решение. Подставив
в уравнение прямой
координаты точки
,
то есть
и
вместо
и
,
получаем:
.
Следовательно,
точка
не лежит на данной прямой
.