Свойства линейных операций над векторами:
1.
2.
3.
4.
5.
6.
7.
8.
,
где
,
,
,
– действительные числа.
Действия над векторами в координатной форме.
Три единичных взаимно перпендикулярных вектора , , пространства, через которые условились выражать все векторы пространства, называются базисными векторами или базисом.
Прямоугольной
декартовой системой координат
в пространстве называется совокупность
точки
и базиса
.
(См. рис. 6)
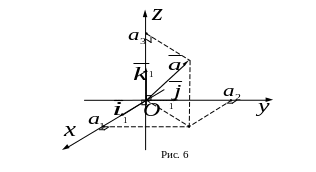
Точка
называется началом координат, оси
,
и
,
проходящие через начало координат –
точку
в направлении базисных векторов
,
и
называются осями координат. Плоскости
,
и
,
проходящие через каждую пару осей
координат называются координатными
плоскостями.
Если выбрана прямоугольная декартова система координат, то любой вектор пространства может быть единственным образом разложен по векторам , , базисным как:
,
то есть для каждого
вектора
пространства в выбранной прямоугольной
декартовой системе координат найдется
единственная тройка чисел – координат
,
что позволяет написать равенство:
(см. рис. 6).
Если два вектора
и
в прямоугольной декартовой системе
координат заданы своими координатами,
то есть
,
,
то
1)
;
2)
.
Пример. Найти
координаты вектора
,
если
,
.
Решение:
.
.
Ответ:
.
Для произвольной
точки
в прямоугольной декартовой системе
координат координатами вектора
являются проекции вектора на оси
,
,
соответственно, то есть
.
(См. рис. 7)
Длина вектора
находится из двух прямоугольных
треугольников
и
:
;
.
Пример. Найти
,
если
.
Решение.
Координаты вектора
:
.
Длина вектора
:
.
Ответ:
.
Скалярное произведение векторов
Скалярным
произведением двух ненулевых векторов
и
называется число, равное произведению
длин векторов на косинус угла между
ними и обозначается:
,
то есть
.
Свойства скалярного произведения:
1)
;
2)
,
;
3)
;
4)
или
.
(2.1)
Пример. Найти
длину вектора
,
если
,
,
.
Решение. По формуле (2.1), находим
.
Ответ:
.
Если два вектора
и
заданы своими координатами:
и
,
то их скалярное произведение находим
по формуле:
.
(2.2)
Пример. Найти
скалярное произведение векторов
и
,
если
и
.
Решение. Координаты векторов и :
;
.
По формуле (2.2) искомое скалярное произведение равно:
.
Ответ:
.
Некоторые приложения скалярного произведения:
1. Угол между двумя ненулевыми векторами и из определения скалярного произведения вычисляется по формуле:
или
(2.3)
Пример. Найти
угол между векторами
и
.
Решение. Координаты
векторов
и
:
и
.
Тогда по формуле (2.3), угол между векторами и равен:
,
следовательно,
,
то есть
.
Ответ:
.
2. Проекция вектора на вектор вычисляется по формуле:
.
Пример. Найти
,
если
и
.
Решение. Координаты
векторов
,
.
Тогда
.
Ответ:
.