Исследование функций и построение их графиков

Одним из приложений производной является ее применение к исследованию функций и построение их графиков.

Рекомендуемая схема исследования функции:

1. Найти область определения функции. Часто полезно учесть множество значений функции.

2. Исследовать специальные свойства функции: четность, нечетность, периодичность, свойства симметрии.

3. Исследовать поведение функции при стремлении аргумента к граничным точкам области определения и к бесконечности, то есть найти асимптоты графика функции: вертикальные и наклонные. Проанализировать расположение графика функции и его асимптот.

4. Найти интервалы монотонности функции: возрастание и убывание. Найти экстремумы функции: минимумы и максимумы.

5. Найти интервалы выпуклости функции и точки перегиба.

6. Найти точки пересечения графика с осями координат.

7. На основании результатов исследования построить эскиз графика.

Симметрия функции

Функция называется четной, если . График четной функции симметричен относительно оси .

Пример. Функция является четной, так как, , следовательно, график этой функции симметричен относительно оси . (См. рис. 57)

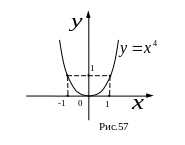
Функция называется нечетной, если . График нечетной функции симметричен относительно начала координат.

Пример. Функция является нечетной, так как , следовательно, график этой функции симметричен относительно начала координат. (См. рис. 58)

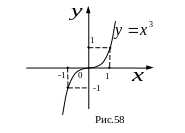
Заметим, что график четной (нечетной) функции достаточно исследовать только при , а при достроить по симметрии, то есть симметрично относительно оси (начала координат).

Функция называется периодической, если существует такое положительное число , что . Наименьшее из таких чисел называется периодом функции. График периодической функции достаточно построить на отрезке оси длины периода , а затем продолжить, сдвигая на , где по оси .

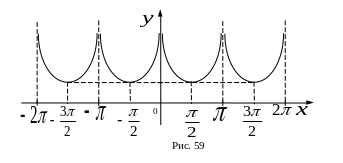
Пример. Функция периодическая с периодом , так как . График этой функции изображен на рис. 59.

Асимптоты графика функции

Прямую называют асимптотой графика функции , если расстояние до точки кривой от прямой стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.

Прямая является вертикальной асимптотой кривой , если .

Прямая является горизонтальной асимптотой кривой , если .

Прямая является наклонной асимптотой кривой , если существуют пределы:

и .

Пример. Найти асимптоты кривой .

Решение. Данная функция определена в интервалах и .

Так как , то прямая есть вертикальная асимптота данной кривой.

Горизонтальных асимптот кривая не имеет, так как предел не является конечной величиной.

Наклонные асимптоты находим в виде уравнения прямой :

;

.

Таким образом, существует наклонная асимптота .

Участки возрастания и убывания функции. Точки минимума и максимума

Функция называется возрастающей (убывающей) на интервале , если для любых точек , таких, что , имеет место неравенство: .

Дифференцируемая на интервале функция возрастает (убывает) на интервале , тогда и только тогда, когда для любого : .

Точка называется точкой максимума (минимума) функции , если:

1) функция определена в некоторой - окрестности точки ;

2) для любого из - окрестности точки справедливо неравенство: (См. рис. 60 и 61).

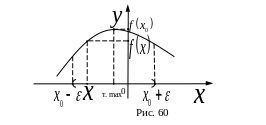
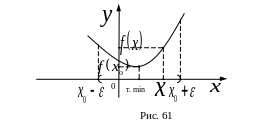
Точки максимума и минимума функции называются точками экстремума функции.

Необходимое условие экстремума: если – точка экстремума функции , то в этой точке либо , либо производная не существует.

Достаточные условия экстремума: пусть функция дифференцируема и непрерывна в – окрестности критической точки кроме, быть может, самой точки , тогда, если ее первая производная меняет знак минус на плюс (плюс на минус) при переходе через точку , то – точка максимума (минимума) функции .

Пример. Найти интервалы монотонности и точки экстремума функции .

Решение. Областью определения данной функции является вся числовая ось , кроме точки , то есть .

Находим первую производную:

.

Используя необходимые условия экстремума, находим критические точки:

или , откуда или .

не существует , откуда .

Используем достаточные условия экстремума. Наносим три критические точки ; ; на область определения функции . Они разбивают область на четыре интервала. Определяем знак функции в каждом интервале.

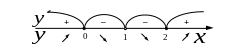
Так как и при переходе через эту точку меняет знак плюс на минус, то – точка максимума функции .

Так как и при переходе через эту точку меняет знак минус на плюс, то – точка минимума функции .

Так как при любом или , то в интервалах и функция монотонно возрастает.

Так как при любом или , то в интервалах и функция монотонно убывает.