Производная сложной функции

Пусть функция определена на множестве , а функция определена на множестве , причем для любой точки , соответствует значение . Тогда на множестве определена функция , которая называется сложной функцией от (или функцией от функции).

Переменную называют промежуточным аргументом сложной функции .

Пример. Функция является сложной функцией, так как , .

Пусть , , тогда – сложная функция с промежуточным аргументом и независимым аргументом . Тогда производная сложной функции по независимой переменной равна произведению производной функции по промежуточной переменной на производную промежуточной переменной по независимой переменной , то есть .

Пример. Найти производную функции .

Решение. Данная функция является сложной, так как , . По правилу дифференцирования сложной функции, находим:

.

Производные высших порядков

Производная функции есть также функция от и называется производной первого порядка.

Если функция дифференцируема, то ее производная называется производной второго порядка и обозначается , то есть .

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается , то есть .

Производной -го порядка (или -й производной) называется производная от производной ( -1)-го порядка и обозначается , то есть .

Пример. Найти производную третьего порядка от функции .

Решение.

,

Итак,

Дифференциал функции

Пусть задана функция и можно вычислить , то есть значение этой функции в точке . Требуется вычислить значение этой функции в точке .

Если данная функция дифференцируема в точке , то в точке существует касательная к графику функции (см. рис. 56). Тогда приращение функции можно представить в виде:

.

Главную часть линейную относительно приращения независимой переменной в последнем равенстве, то есть выражение называют дифференциалом функции в точке и обозначают . Итак, .

При , то есть при приращение функции приближенно равно дифференциалу :

или .

Последнюю формулу применяют для приближенного вычисления значений функций в точке.

Пример. Вычислить .

Решение. Рассмотрим функцию . Пусть , тогда , откуда .

,

.

Следовательно, .

Ответ: .

Заметим, что дифференциал независимой переменной равен ее приращению, то есть , так как . Таким образом, дифференциал функции вычисляется по формуле:

.

Пример. Найти дифференциал функции .

Решение. , тогда .

Правило Лопиталя

Рассмотрим способ раскрытия неопределенностей вида и при вычислении пределов от функции одного переменного, который основан на применении производных.

Пусть функции и непрерывны и дифференцируемы в окрестности точки и обращаются в нуль в этой точке: . Пусть в окрестности точки . Тогда, если существует предел , то .

Пример. Вычислить предел .

Решение.

.

Пусть функции и непрерывны и дифференцируемы в окрестности точки (кроме, быть может, самой точки ), в этой окрестности , . Тогда, если существует предел , то .

Пример. Вычислить предел .

Решение.

.
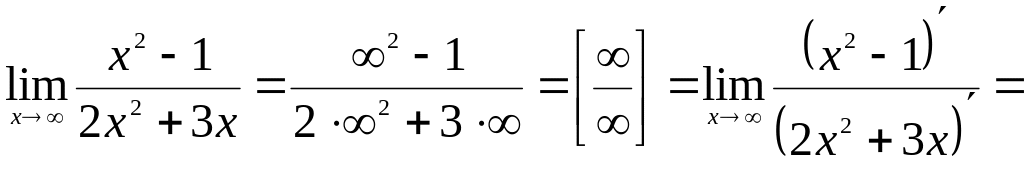
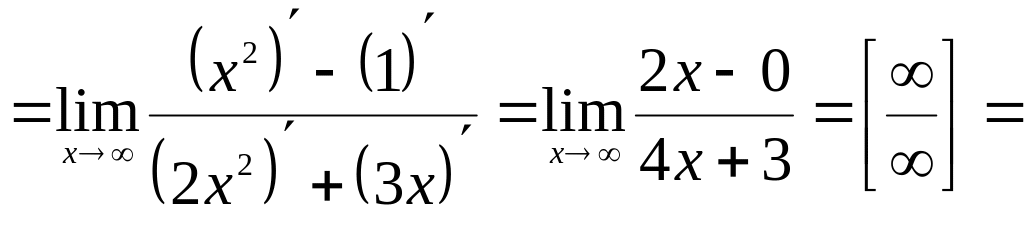