Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Нижегородский государственный архитектурно-строительный университет»

-------------------------------------------------------------------------------------------------

Институт экономики, управления и права

П.В. Столбов Математика

Часть I

Утверждено редакционно-издательским

советом университета в качестве

учебного пособия

Нижний Новгород

ННГАСУ

2013

ББК 22.1

С 81

Столбов П.В. Математика. Часть I [текст]: учебное пособие / П.В. Столбов; Нижегород. гос. архит.-строит. ун-т.– Н.Новгород: ННГАСУ, 2013. – 83 с.

ISBN 978-5-87941-880-2

Учебное пособие и контрольные задания по математике предназначены для студентов заочной формы обучения всех специальностей и направлений.

ББК 22.1

ISBN 978-5-87941-880-2

© Столбов П.В., 2013

© ННГАСУ, 2013

§ 1. Линейная алгебра Матрицы и действия над ними

Матрицей порядка называется прямоугольная таблица чисел, состоящая из строк и столбцов.

Для обозначения матрицы таблицу чисел заключают в круглые скобки и обозначают заглавными буквами латинского алфавита.

Пример.

1. – матрица порядка .

2. – матрица – строка порядка .

3. – матрица – строка порядка .

Матрица, в которой число строк совпадает с числом столбцов, называется квадратной.

Пример. – квадратная матрица порядка .

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы, обозначаются соответствующими строчными буквами латинского алфавита с двумя правыми нижними индексами. Первый индекс обозначает номер строки, а второй – номер столбца, в которых рассматриваемый элемент матрицы находится.

Пример. .

–элемент матрицы , находящийся во второй строке и в третьем столбце.

Заметим, что матрицу порядка можно записать так:

, ; .

Две матрицы порядка считаются равными, если все соответствующие элементы этих матриц равны. То есть , если для любых возможных и .

Пример. 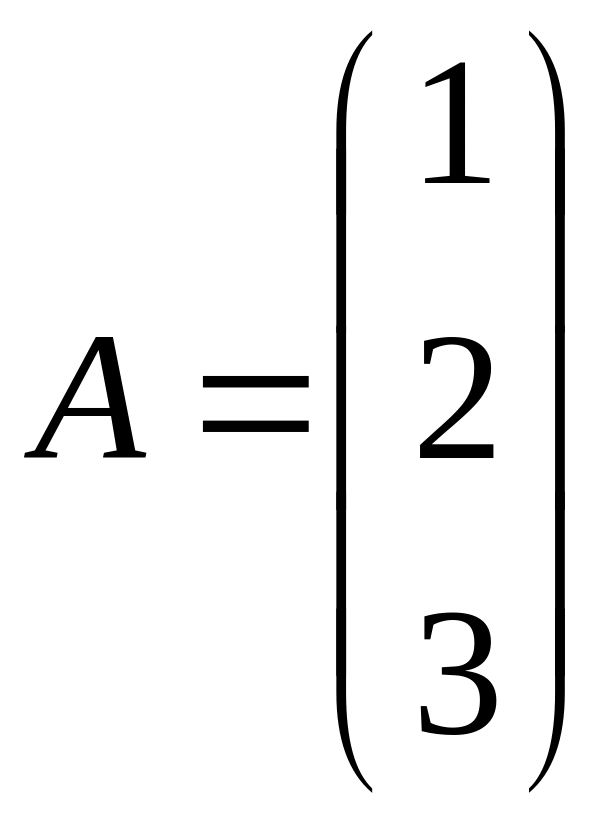, . Матрицы и равны, так как , , .

Произведением матрицы порядка на действительное число называется матрица того же порядка , каждый элемент , , которой получен умножением соответствующего элемента , , исходной матрицы на число и обозначается: .

Пример. Найти , если .

Решение. .

Ответ: .

Суммой двух матриц и одного порядка называется матрица того же порядка , каждый элемент , , которой получен сложением соответствующих элементов и , , и обозначается .

Пример. Найти , если и .

Решение. .

Ответ: .

Заметим, что разность двух матриц и одного и того же порядка можно определить через сумму и умножение на число , то есть .

Пример. Найти , если и .

Решение.

.

Ответ: .

Произведением матрицы порядка на матрицу порядка называется матрица порядка , каждый элемент , , которой получен как произведение элементов -ой строки матрицы на соответствующие элементы -го столбца матрицы , то есть , , и обозначается: .

Пример. Найти , если и .

Решение.

.

Следовательно, .

Ответ: .

Следует обратить внимание на тот факт, что:

1) произведение матриц и получается умножением элементов строк матрицы – первого сомножителя – на элементы столбцов матрицы – второго сомножителя. Следовательно, порядок сомножителей в произведении матриц важен;

2) число столбцов матрицы должно быть равно числу строк матрицы , в противном случае произведение матриц и не определено;

3) порядок матрицы-произведения определяется порядком сомножи-телей, то есть . Следовательно, если , то нельзя считать, что .

Транспонированной матрицей (обозначаемой как ) любой матрицы порядка называется матрица порядка , которая получается из матрицы взаимной заменой строк на столбцы.

Пример. Найти , если .

Решение. Элементы первой строки матрицы запишем в первый столбец матрицы , а элементы второй строки матрицы – во второй столбец матрицы , получаем: .
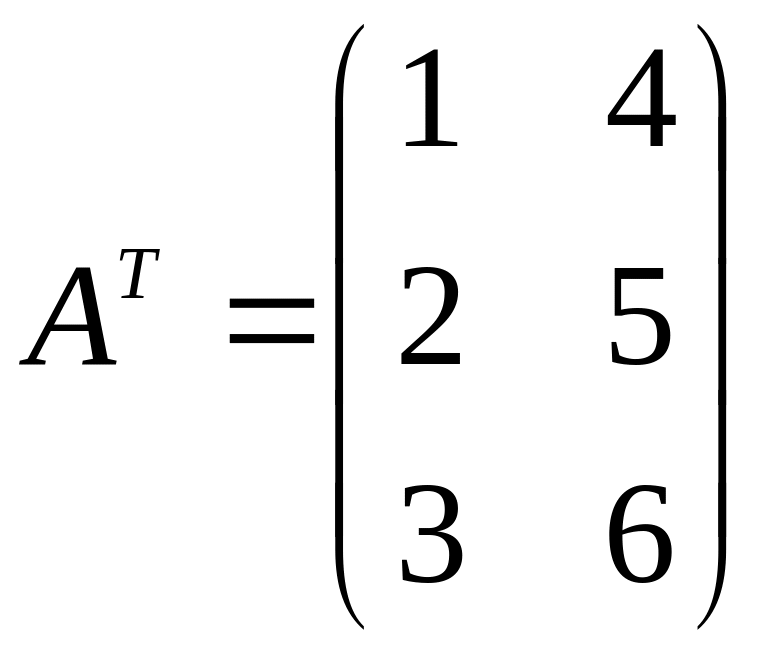