Точечная оценка показателей риска

Показатель оценки риска - вероятность получения фактического значения результата, меньше требуемого значения (намеченного, планируемого, прогнозируемого):  

R = p· (х < Д_тр),

      где R – показатель (функция распределения) оценки риска;     p – вероятность риска;     Д_тр – требуемое (планируемое) значение результата – действительное число;     х – текущее значение результата как случайной величины.

Для использования данного показателя, необходимо знать тип и параметры закона распределения значений результатов деятельности. Полагая, что на результат предпринимательской деятельности влияет большое количество внешних и внутренних факторов риска, используют гипотезу, что результат (как случайная величина) подчинен нормальному закону или близкому к нормальному закону распределения.

Кривая функции плотности нормального распределения представлена на рис. 1, и представляет собой графическое изображение зависимости плотности распределения вероятностей от возможных значений результата. Из кривой можно увидеть, что значения результата наиболее тесно группируются вокруг величины (кривая плотность в этой точке максимальна), а по мере убывания влево и вправо значений результатов их плотность падает.  

Рис. 1. Точечная оценка риска

В частности, показатель риска (вероятность получения результата не ниже требуемого) определяется площадью под кривой, которая для нормального закона распределения равна:  

,

 где x, σ - числовые характеристики распределения: математическое ожидание и дисперсия.

Для построения кривых плотности распределения вероятностей возможных результатов предпринимательской деятельности требуется достаточно объемный массив статистической информации, чтобы проверить статистические гипотезы о виде и параметрах закона распределения. Зачастую такие исходные данные получить заранее сложно, поэтому вероятностные показатели в предложенном виде используют редко.

Интервальная оценка показателя риска

Точечная оценка риска не имеет информации о точности процедуры оценивания. Поэтому предпринимателю, оценивающему риск своей деятельности, необходим и интервальный подход, заключающийся в определении вероятности получения результата в заданных пределах.

В частности, вероятность того, что результат примет значения, принадлежащие интервалу [х₁;х₂], равна:  

R = p·(x₁ ≤ x ≤ x₂) = F(x₂) - F(x₁),

или

  ,

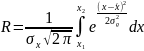 Графическая интерпретация полученного выражения представлена на рис.2.  

 

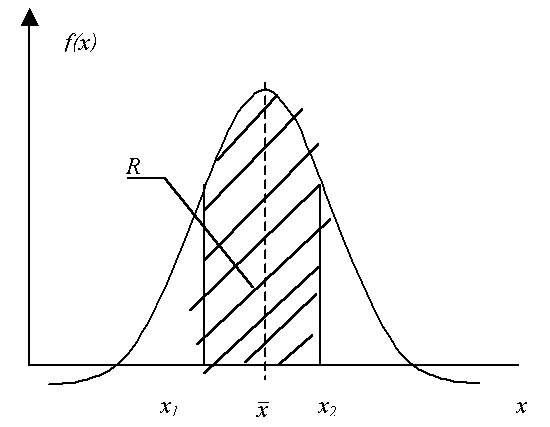
Рис. 2. Интервальная оценка риска

Интервальное оценивание уровня риска является основой концепции рисковой стоимости. Величина рисковой стоимости как обобщающая оценка рыночного риска нужна в первую очередь для принятия оперативных решений высшим руководством компании.  

Интервальное оценивание уровня риска является универсальной методикой расчета различных видов риска:

   1. Ценового риска — риска изменения стоимости цены финансового актива на рынке;   2. Валютного риска — риск, связанный с изменением рыночного валютного курса национальной валюты к валюте другой страны;   3. Кредитного риска — риска, возникающего при частичной или полной неплатежеспособности заемщика по взятому кредиту;   4. Риска ликвидности — риска, связанного с невозможностью продажи финансового актива либо с большими убытками, возникающими при продаже актива в силу большой разницы величины при покупке или продаже, существующей на рынке.

Рисковая стоимость отражает максимально возможные убытки от изменения стоимости финансового инструмента, портфеля активов, которое может произойти за данный период времени с заданной вероятностью его появления.

Из определения следует, что ключевыми показателями при рисковой стоимости являются уровень доверительного интервала (доверительной вероятности) и временной горизонт.

Уровень доверительного интервала – это граница, которая отделяет «нормальные» колебания рынка, от экстремальных ценовых всплесков по частоте их проявления. Обычно вероятность потерь устанавливается в пределах 1 – λ= {1,0; 2,5 или 5%} (соответствующий уровень доверительного интервала составляет g = {99; 97,5 или 95%}). Следует учитывать, что с увеличением уровня доверительного интервала показатель рисковой стоимости будет возрастать: очевидно, что потери, случающиеся с вероятностью лишь 1%, будут выше, чем потери, возникающие с вероятностью 5%.

Выбор временного горизонта зависит от того, насколько часто производятся сделки с данными активами, а также от их ликвидности. Для финансовых институтов, ведущих активные операции на рынках капитала, типичным периодом расчета является один день, тогда как стратегические инвесторы могут использовать и большие периоды времени.

Вместе с удлинением временного горизонта возрастает и показатель рисковой стоимости. Понятно, что возможные прибыли и убытки, например за пять дней, могут иметь большие масштабы, чем за один день. На практике считают, что за период в n дней, величина рисковой стоимости будет приблизительно в раз больше, чем за один день.

Статистические показатели оценки риска

 Статистические показатели по своей информативности несколько уступают вероятностным, так как в основе своей являются параметрами соответствующих законов распределения и требуют меньшего объема исходной информации для оценивания уровня риска.

По своему предназначению данная группа оценивает:     — среднее значение ожидаемого результата деятельности предпринимателя, например, прибыли;     — изменчивость возможного результата деятельности относительно среднего ожидаемого значения.  

Среднее значение ожидаемого результата деятельности

Модели расчета данных показателей различаются в зависимости от предполагаемых вариантов их использования. Если результаты расчетов по наблюдаемым значениям будут экстраполированы в будущее без существенных изменений, то используется средняя величина вида:

,

    где х_i – i - е значение случайной величины;

n – число наблюдений.

В случае же коррекции наблюдаемых значений используется средневзвешенная величина из всех возможных значений результата х_i и вероятностей р_i его появления:  

 

Показатели вариации уровня риска.