Московский Государственный Технический Университет им. Н.Э. Баумана

Кафедра СМ3

«Динамика и управление полётом ракет и космических аппаратов»

Курсовая работа

По курсу «Динамика полёта летательных аппаратов»

«Продольное сбалансированное движение неуправляемой ракеты

с учётом влияния ветра »

Вариант №15

Выполнил студент: Скубицкий М.В.

Группа: СМ3-71

Преподаватель: Казаковцев В.П.

Москва 2014

Оглавление

1. Постановка задачи………………………………………………………..………………………..…..……………..3

2. Исходные данные…………………………………………………………………………………………………..…..4

3. Математическая модель…………………………………………………………………………………………….5

4. Программа расчёта параметров номинальной траектории…………………………….……….8

5. Расчёт номинальной траектории…………………………………………………………………………………………..13

6. Расчёт отклонений координат точек падения по дальности стрельбы при действии возмущений……………………………………………………………………………….………………………….….18

7. Расчёт отклонений координат точек падения по дальности стрельбы при наличии ветра……………………………………………………………………………………….………………………………...20

8. Заключение о влиянии различных параметров на дальность стрельбы………….…… 31

1.Постановка задачи.

1. Сформировать математическую модель продольного, сбалансированного движения неуправляемой баллистической ракеты.

2. Разработать программу расчёта параметров траектории движения неуправляемой баллистической ракеты.

3. Провести расчёт параметров номинальной траектории и построить графики , , , .

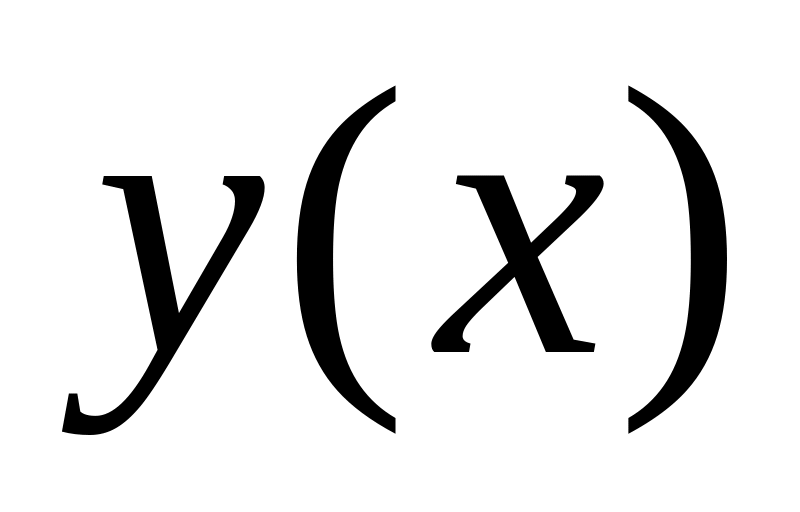Рассчитать величины отклонений координат точек падения по дальности стрельбы при действии следующих возмущений (со знаком плюс и минус): V_кo = 5 м/с, _o = 0,1 град, m_o = 5 кг, m_т = 2 кг, W_e = 10 м/с, t_к = 0,1 сек, /_ст = 0,05, C_x / C_x =0,05.

4. Определить соответствующие поправочные коэффициенты.

5. Провести расчёты отклонений координат точек падения по дальности стрельбы при наличии ветра ( ):

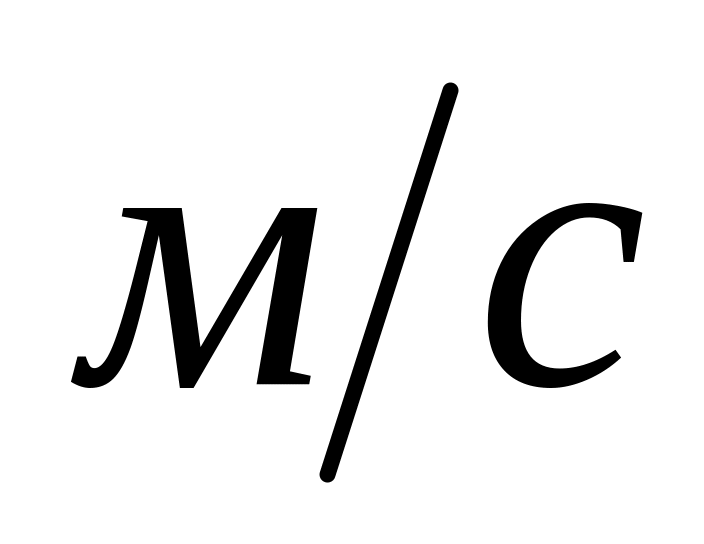- только на активном участке траектории;

- только на пассивном участке траектории;

- на всей траектории.

Построить графики .

6. Написать заключение о влиянии различных возмущающих факторов на отклонения координаты точки падения по дальности стрельбы.

2. Исходные данные.

d_м = 0.16м - диаметр миделя ракеты;

d_a = 0.15 м - диаметр выходного сечения сопла двигателя;

m₀ = 160 кг - начальная масса ракеты;

m_k = 128 кг - конечная масса ракеты;

t_k = 5.2 c - время активного участка;

W_e = 2420 м/с - эффективная скорость истечения топлива;

V_ko = 52 м/с - начальная траекторная скорость;

Θ₀ = 46 град - начальный угол наклона траектории.

3.Математическая модель.

Продольное движение неуправляемой баллистической ракеты рассматриваем в нормальной земной системе координат с учетом следующих допущений:

1. Ракета является осесимметричным, статически устойчивым твёрдым телом переменной массы.

2. Продольная ось ракеты в любой момент времени направлена по вектору воздушной скорости (сбалансированное движение).

3. Кривизна Земли не учитывается.

4. Динамические уравнения движения центра масс ракеты записываются в проекциях на касательную и нормаль к траектории.

- траекторная скорость;

- скорость относительно подвижной атмосферы;

- скорость продольного горизонтального ветра;

- угол наклона траекторной скорости;

- угол между воздушной и траекторной скоростями;

- сила тяжести;

-сила тяги;

- сила лобового сопротивления.

При заданных допущениях дифференциальные уравнения продольного движения неуправляемой ракеты можно записать в следующем виде:

Уравнения связи, позволяющие определить кинематические параметры:

, - угол между векторами воздушной и траекторной скоростей,

- воздушная скорость,

- скоростной напор,

- число Маха,

- продольная перегрузка.

Формулы для определения сил, действующих на ракету:

1) - сила тяги, где:

- сила тяги в пустоте,

-давление воздуха;

- эффективная скорость истечения газов,

- секундный расход массы топлива,

, - начальная и конечная массы ракеты,

- время работы двигателя,

- площадь выходного сечения сопла двигателя;

2) - сила тяжести, где:

- текущая масса ракеты,

- ускорение силы тяжести;

3) - сила лобового сопротивления, где:

- площадь миделевого сечения,

- скоростной напор,

- аэродинамический коэффициент силы лобового сопротивления,

-плотность воздуха.

Для неуправляемых ракет небольшой дальности аэродинамический коэффициент силы лобового сопротивления задается таблично в зависимости от числа Маха для активного (АУТ) и для пассивного (ПУТ) участков траектории:

Таблица 1. Величины аэродинамических коэффициентов силы лобового сопротивления.

M	0	0,25	0,5	0,75	0,9	1,0	1,10	1,25	1,5	2,0	3,0
Cx (АУТ)	0,30	0,30	0,31	0,38	0,51	0,56	0,59	0,58	0,52	0,44	0,42
Cx (ПУТ)	0,32	0,32	0,33	0,41	0,54	0,60	0,63	0,62	0,56	0,49	0,46

Текущие значения величин аэродинамических коэффициентов определяют путём линейной интерполяции:

, ,

где значения чисел Маха из соседних столбцов таблицы.

Параметры атмосферы определяются по таблицам и формулам стандартной атмосферы (ГОСТ 4401-81). Для неуправляемых баллистических ракет, высота которых менее десяти километров, можно использовать следующие формулы расчета параметров атмосферы:

- температура воздуха (y(м) - высота полета), К;

- давление воздуха, Па;

- плотность, кг/м³;

- скорость распространения звука, м/с.