Вариант 10
В ящике содержатся 10 одинаковых деталей, помеченных номерами 1, 2,..., 10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажется деталь с номером 1.
В ящике 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
Экзаменационный билет содержит три вопроса. Вероятности того, что студент ответит на первый, второй и третий вопросы, соответственно равны 0.9, 0.9, 0.8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса.
Дан закон распределения дискретной случайной величины:
x: |
515 |
525 |
535 |
545 |
555 |
p: |
0.1 |
0.02 |
0.18 |
0.38 |
0.32 |
вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение.
Дана функция распределения непрерывной случайной величины Х :
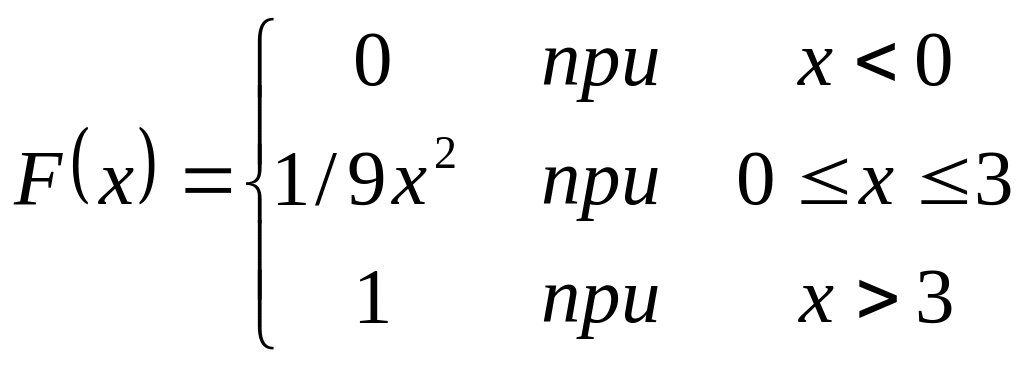
Найти плотность распределения f(x), построить ее график, вероятность попадания в заданный интервал, Mx, Dx, .
6. Задано распределение вероятностей дискретной двумерной случайной величины:
Y X |
26 |
30 |
41 |
50 |
1,6 |
0,05 |
0,12 |
0,08 |
0,04 |
2,7 |
0,09 |
0,30 |
0,11 |
0,21 |
Найти законы распределения составляющих, коэффициент корреляции.
Для изучения количественного признака Х из генеральной совокупности извлечена выборка х1, х2,…,хп, объема п, имеющая данное ниже статистическое распределение.
а) Построить полигон частот по данному распределению выборки.
б) Найти выборочное среднее , выборочное среднее квадратичное отклонение и исправленное среднее квадратичное отклонение S.
в) При данном уровне значимости проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности.
х |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
п |
4 |
7 |
11 |
18 |
24 |
22 |
15 |
9 |
6 |
4 |