Специальность 270800 Контрольная работа №6 по математике преп. Дубровский В.В.

Теория вероятностей и математическая статистика

.

.

Вариант 1

1. В некотором городе утро в июле может быть либо ясным, либо пасмурным. Наблюдения показали: если июльское утро ясное, то вероятность дождя в этот день равна 0,1; если июльское утро пасмурное, то вероятность дождя в этот день равна 0,5. Вероятность того, что утро в июле будет пасмурным равна 0,2. Найти вероятность того, что в случайно взятый июльский день дождя не будет.

2. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков. Вероятность рождения мальчика принять равной 0,51.

3. Три стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка – 0.7, для второго – 0.5, для третьего – 0.4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что попал второй стрелок.

4. Дан закон распределения дискретной случайной величины:

x:	32	37	47	52	57
p:	0.25	0.15	0.45	0.05	0.1

вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение.

5. Дана функция распределения непрерывной случайной величины Х

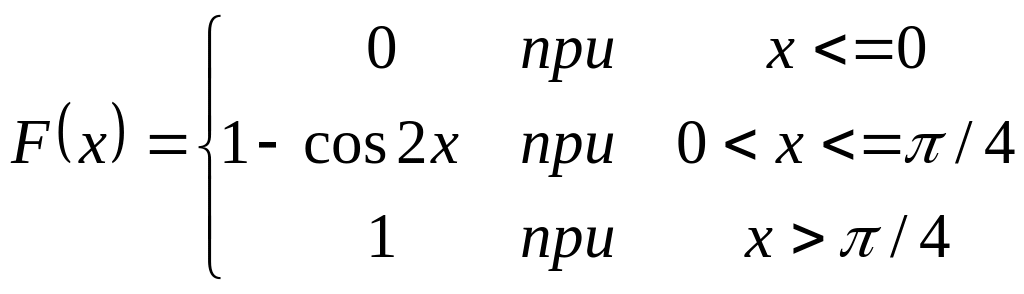
Найти плотность распределения f(x), построить ее график, вероятность попадания в заданный интервал , Mx, Dx, .

6. Задано распределение вероятностей дискретной двумерной случайной величины:

Y X	2	5	8
7,4	0,15	0,30	0,35
7,8	0,05	0,12	0,03

Найти законы распределения составляющих, коэффициент корреляции.

7. Для изучения количественного признака Х из генеральной совокупности извлечена выборка х_1, х_2,…,х_п, объема п, имеющая данное ниже статистическое распределение.

а) Построить полигон частот по данному распределению выборки.

б) Найти выборочное среднее , выборочное среднее квадратичное отклонение и исправленное среднее квадратичное отклонение S.

в) При данном уровне значимости проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности.

х	2	3	4	5	6	7	8	9	10	11
п	1	6	10	16	20	21	17	11	7	1

Вариант 2

1. Монету подбрасывают независимо друг от друга 5 раз. Найти вероятность того, что герб выпадет менее 2-х раз.

2. В ящике находятся 12 деталей, изготовленных на заводе № 1, 20 деталей – на заводе № 2 и 18 деталей – на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества – равна 0.9; для деталей, изготовленных на заводах № 2 и № 3, эти вероятности равны 0.6 и 0.9. Наудачу берется деталь. Найти вероятность того, что она окажется отличного качества.

3. По мишени стреляют независимо друг от друга 3 человека, вероятности попадания каждого из них в цель соответственно равны 0.6; 0.5; 0.4. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежит первому стрелку.

4. Дан закон распределения дискретной случайной величины:

x:	45	70	95	120	145
p:	0.1	0.2	0.5	0.1	0.1

вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение.