Изучение явления зеебека

Цель работы: 1. Теоретическое знакомство с явлением преобразования тепловой энергии в электрическую при контакте разнородных металлов и применение основных законов изучаемого явления на практике.

2. Проверка I и II законов Вольта.

Приборы и принадлежности: термопары, магазин сопротивлений, гальванометр, электроплитка, термометр.

Теория вопроса

Электроны проводимости в металле находятся в беспорядочном тепловом движении. Наиболее быстро движущиеся электроны, обладающие достаточно большой кинетической энергией, могут вырываться из металла в окружающее пространство. При этом они совер­шают работу как против сил притяжения со стороны избыточного положительного заряда, возникающего в металле в результате их вылета, так и против сил отталкивания со стороны ранее вылетев­ших электронов, образующих вблизи поверхности проводника электронов «облако». Между электронным газом в металле и электронным «облаком» существует динамическое равновесие.

Недостаток электронов в металлическом проводнике и их из­быток в окружающем пространстве, образовавшиеся в результате вылета части электронов из металла, проявляются только в очень тонком слое по обе стороны от поверхности проводника. Толщина этого слоя равна нескольким межатомным расстояниям в металле. В первом приближении можно считать, что поверхность металла представляет собой двойной электрический слой, подобный весьма тонкому конденсатору.

Электрон, вылетая за пределы металла, должен преодолеть задерживающее его электрическое поле двойного слоя. Работу, которую нужно совершить для удаления электрона из металла в безвоздушное пространство, называют работой выхода А. Характеризующую это поле разность потенциалов Δφ принято называть поверхностным скачком потенциала, контактной разностью потенциалов между металлом и окружающей средой или потенциалом выхода .

, (1)

где e – заряд электрона.

Работа выхода зависит от химической природы металла и состояния его поверхности: загрязнения, следы влаги и пр. изменяют ее величину. Для чистых металлов работа выхода колеблется в пределах нескольких электронвольт.

Р и с у н о к 1

Рассмотрим контакт различных металлов 1 и 2 (рисунок 1). Обозначим работу выхода электронов из первого металла А₁, концентрацию электронов в нем n₀₁; для второго металла соответственно А₂ и n₀₂ .

Пусть . При этих условиях наиболее быстрые электроны при хаотическом тепловом движении будут преимущественно переходить через поверхность контакта из первого металла во второй, в результате чего в первом металле появится их недостаток, и ме­талл I зарядится положительно, а во втором - их избыток, и металл 2 зарядится отрицательно. Избыточный положительный заряд в 1-ом металле и избыточный отрицательный заряд во 2-ом распределяются вблизи поверхностей металлов, которые будут являться зквипотенцальными. Таким образом, возникает контактная разность потенциалов (к.р.п.).

При определенных условиях наступит равновесие. Пусть потенциал точки внутри металла 1 вблизи его поверхности равен , а вне металла – . Для металла 2 – соответственно – и . К.р.п. между, точками, лежащими внутри металлов вблизи их поверхности называется внутренней к.р.п., а между точками вне металла – внешнeй к.р.п. .

Внешняя контактная разность потенциалов к.р.п. связана с различием в работах выхода электрона из металлов.

Внешняя к.р.п. равна

(2)

Внутренняя к.р.п. связана с различием концентрации электронов в различных металлах. Согласно теоретическим расчетам

(3)

где k  постоянная Больцмана, Т  температура.

ЗАКОН ВОЛЬТА И ТЕРМОЭЛЕКТРОДВИЖУЩАЯ СИЛА

Внешняя контактная разность потенциалов практически не зависит от температуры и равна нескольким вольтам. Внутренняя контактная разность потенциалов примерно на три порядка меньше и почти линейно зависит от температуры (формула 3). Формулы (2) и (3) являются математическим выражением I закона Вольта, который был установлен экспериментально в 1797г. и говорит о том, что к.р.п. зависит от химической природы металлов ( ) и от температуры соприкасающихся металлов Т. Следует обратить внимание, что ранее не было разделения на внешнюю и внутреннюю к.р.п., а говорили просто о к.р.п.

II Закон Вольта гласит: контактная разность потенциалов последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна к.р.п. возникающей при не­посредственном соединении крайних проводников. Для доказательства этого закона приведем в соприкосновение четыре разнородных проводника при одинаковой температуре (рисунок 2).

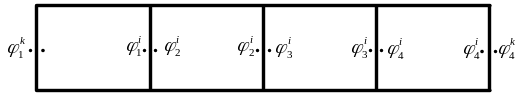
Р и с у н о к 2

Разность потенциалов между концами разомкнутой цепи равна алгебраической сумме скачков потенциала во всех контактах:

т.е. действительно не зависит от природы промежуточных проводников.

Возьмем замкнутую разнородную цепь, состоящую из 3-х проводников, находящихся при одинаковой температуре, как показано на рисунке 3.

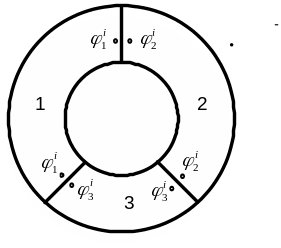
Р и с у н о к 3

Обходя цепь, например, по часовой стрелке получим:

(4)

Таким образом, при образовании замкнутой цепи из нескольких металлических проводников с одинаковой температурой спаев невозможно возникновение электродвижущей силы только за счет контактных скачков потенциала.

Если же температуры контактов будут разные, то алгебраичес­кая сумма скачков потенциала на контактах будет не равной нулю, т.к. внутренняя контактная разность потенциалов зависит от температуры (формула (3)), и в цепи возникает электрический ток, называемый термоэлектрическим (явление Зеебека).

Рассмотрим замкнутую цепь из двух металлов 1 и 2 с температурами спаев Т_а и T_b, причем Т_а>T_b (рисунок 4).

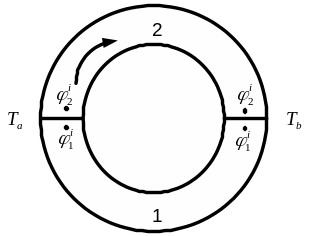
Р и с у н о к 4

Таким образом, сумма контактных разностей потенциалов в замкнутой цепи, состоящей из разнородных металлов при различных температурах контактов, отлична от нуля. Т.е. в такой цепи появляется э.д.с., прямо пропорциональная разности температур в контактах. Эта э.д.с. называется термоэлектродвижущей силой

(5)

Коэффициент зависит от свойств контактирующих металлов, поэтому обозначим его , тогда:

(6)

где – называется удельной термо-э.д.с., т.е. термо-э.д.с., возникающей в цепи при разности температур контактов в один градус, или коэффициентом термо-э.д.с., который является характе­ристикой обоих металлов термопары.

На практике это создает определенные неудобства. Для избе­жания их условились величину измерять по отношение к од­ному и тому же металлу, за который принимается свинец. Это означает, что измеряется для термопары, у которой одна ветвь составлена из исследуемого материала, а другая – из свинца.

Коэффициент термоэлектродвижущей силы металла 1 по отношению к металлу 2 определяется по формуле:

где и – значения коэффициентов т.э.д. силы металлов 1 и 2 соответственно по отношению к свинцу; – величина алгебраическая. Знак у  введен для определения направления термотока и обозначает, что в нагретом спае ток течет от металла с меньшим значением  (алгебраически) к другому. Т. e., если в нагретом спае потенциал металла 1 повышается, а потенциал металла 2 понижается, то величина  считается положительной.

Очевидно, справедливо соотношение .

Явление возникновения термо-э.д.с. можно наблюдать и при контакте полупроводников.

Удельная термо-э.д.с. у полупроводниковых пар разного типа на 2 порядка больше, чем у металлических пар и нелинейно зависит от температуры, что объясняется сильной зависимостью концентрации свободных зарядов в полупроводниках от температуры образца, а также более резкой зависимостью сопротивления полупроводников от температуры. К.п.д. полупроводниковой пары больше, чем у метал­лов. Он достигает 10–18 %. Это объясняется также и малой теплопро­водностью полупроводников.