Применение определителя Вандермонда для получения аналитической функции, описывающие переходные процессы пуска ненагруженной эмс до номинальной частоты вращения дпт нв
Собственные значения матрицы переменных состояний :
определитель Вандермонда и составляющие матричной функции F(t):
Матричная функция и временные характеристики:
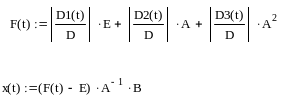
Рисунок 18 – Зависимость i(t), найденная с помощью определителя Вандермонда
Рисунок 19 – Зависимость , найденная с помощью определителя Вандермонда
Находим перерегулирование:
Оно совпадает с перерегулированием, которое получено в предыдущем расчете.
Рисунок 20 –
Зависимость
,
найденная с помощью определителя
Вандермонда
12.Определения показателей качества для аналитических функций скорости двигателя от времени рассмотренных методов
1.Для Классического метода.
Время переходного процесса определим как последние пересечение функции скорости с пятипроцентной зоной.
Рисунок 24 –
Графическое определения время переходного
процесса для
В данном примере для точного нахождения tпп воспользуемся методом касательных.
Для определения времени достижения функцией первого максимума возьмем производные от по t:
Рисунок 25 – Графическое изображение производной
Время нарастания до установившегося значения:
Рисунок 26 – Графическое изображение переходного процесса
Рисунок 27 – Графические определения времени нарастания до установившегося значения для .
Определим установившееся значение :
Определим перерегулирование:
2. Для Операторного метода.
Время переходного процесса определим как последние пересечение функции скорости с пятипроцентной зоной.
Рисунок 28 –
Графическое определения время переходного
процесса для
В данном примере для точного нахождения tпп воспользуемся методом касательных.
Для определения времени достижения функцией первого максимума возьмем производные от по t:
Рисунок 29 – Графическое изображение производной
Время нарастания до установившегося значения:
Рисунок 30 – Графическое изображение переходного процесса
Рисунок 31 – Графические определения времени нарастания до установившегося значения для .
Определим установившееся значение :
Определим перерегулирование:
3.Для определителя Вандермонда.
Время переходного процесса определим как последние пересечение функции скорости с пятипроцентной зоной.
Рисунок 32 –
Графическое определения время переходного
процесса для
В данном примере для точного нахождения tпп воспользуемся методом касательных.
Для определения времени достижения функцией первого максимума возьмем производные от по t:
Рисунок 33 – Графическое изображение производной
Время нарастания до установившегося значения:
Рисунок 34 – Графическое изображение переходного процесса
Рисунок 35 – Графические определения времени нарастания до установившегося значения для .
Определим установившееся значение :
Определим перерегулирование:
Сведем показатели качества переходного процесса скорости, полученные методом касательных, в таблицу 1.
Таблица 1 – Показатели качества переходного процесса скорости, полученные методом касательных
Показатель |
Методы расчета |
||
Классический |
Операторный |
Вандермонда |
|
Время переходного процесса, с |
0,2 |
0,2 |
0,2 |
Время достижения первого максимума, с |
0,077 |
0,077 |
0,077 |
Перерегулирование, % |
4,14 |
4,14 |
4,14 |