3. Составление структурной схемы эмс

Рисунок 3 – Структурная схема электромеханической системы с ПИ-регулятором и силовым преобразователем, описанным как пропорциональное звено

4. Настройка регулятора скорости

Имитационная модель линейной одноконтурной ЭМС в программной среде Classic представлена на рисунке 4.

Рисунок 4 – Имитационная модель линейной одноконтурной ЭМС в программной среде Classic

Рисунок 5 – Переходный процесс скорости в неоптимизированной ЭМС

Рисунок 6 – Показатели качества неоптимизированной ЭМС

Данное перерегулирование по скорости для рассматриваемой системы находится в допустимых пределах.

Рисунок 7 – Корневая плоскость ЭМС

Рисунок 8 – Численные значения корней характеристического уравнения ЭМС

Рисунок 8– Переходный процесс тока ЭМС

5. Составление в нормальной форме Коши системы дифференциальных уравнений, описывающих состояние эмс

Электромеханическая система с ПИ-регулятором и силовым преобразователем, описанным как пропорциональное звено, описывается системой из трех дифференциальных уравнений:

Запишем систему в нормальной форме Коши:.

6. Составление системы дифференциальных уравнений, описывающие состояние эмс, в матричной форме

Представим систему в матричном виде:

Матрица коэффициентов в общем виде:

Матрица свободных членов в общем виде:

7. Решение задачи Коши для ненагруженной эмс с нулевыми начальными условиями классическим способом.

Найдем собственные значения матрицы А с помощью программы MathCAD:

Единичная матрица

Критерием правильности выполнения расчетов является совпадение корней полученных в программе Classic с корнями, полученными при расчете классическим способом.

При совпадении корней продолжается расчет

Для каждого полученного собственного значения составляем СЛАУ.

Для действительного собственного значения λ0= –23,59:

Принимаем значение .Выражаем из второго и третьего и

При комплексно-сопряженных собственных значениях достаточно найти вектор только для одного из них, что мы и делаем для λ1= –26,41-46,28i

Принимаем значение .Выражаем из второго и третьего и

Общее решение однородной системы запишется в виде:

где N₁, N₂, N₃ – константы интегрирования.

Найдем частное решение неоднородной системы:

Или

Частное решение находим в момент, когда ЭМС работает в статическом режиме при .Учитывая это условие, считаем что производные функций равны нулю.

Где Хчаст - частное решение неоднородной системы.

Определяем частное решение методом Крамера:

Также частное решение можно найти методом обратных матриц:

Где Хchast- частное решение неоднородной системы.

Записываем общее решение СДУ:

Решим задачу Коши, при нулевых начальных условиях:

Т.к t=0, то i(0),w(0)=0,U(0)=0

Находим постоянные интегрирования методом Крамера:

Постоянные интегрирования можно найти также при помощи метода обратных матриц:

Несмотря на громоздкость метода Крамера по сравнению с методом обратных матриц он также используется при расчетах.

Подставим постоянные интегрирования:

При помощи построения графиков можно наглядно увидеть переходные процессы. Зависимости тока, скорости и напряжения от времени.

Рисунок 9– Переходный процесс тока ЭМС

Рисунок 10 – Переходный процесс скорости в неоптимизированной ЭМС

Критерием правильности выполнения расчетов является совпадение перерегулирования полученного в программе Classic, с перерегулированием, полученным при расчете классическим способом.

При совпадении перерегулирований расчет продолжается.

Рисунок 11 – Переходный процесс. Зависимость напряжения от времени

Полученные характеристики полностью совпали с аналогичными графиками, полученными в программной среде Classic.

8. Применение прямое преобразование Лапласа с ненулевыми начальными условиями получить СЛАУ, описывающих состояние ЭМС с использованием изображений управляющего воздействия и переменных СЛАУ. Получение изображения переменных состояния при пуске ненагруженной ЭМС

Система дифференциальных уравнений в каноническом виде:

Применяя прямое преобразование Лапласа при нулевых начальных условиях, получаем систему линейных алгебраических уравнений (СЛАУ):

Представим СЛАУ в виде А(р)х(р)=В(р):

Подставляя численные значения параметров системы, получаем:

Решим СЛАУ методом Крамера в программе MathCAD:

Изображения функций:

Применяя обратное преобразование Лапласа, найдем оригиналы функций, описывающих переходный процесс пуска ненагруженной ЭМС, и построим их графики:

Рисунок 12 – Зависимость i(t), найденная операторным методом

Рисунок 13 – Зависимость , найденная операторным методом

Находим перерегулирование:

Оно совпадает с перерегулированием, которое получено в предыдущем расчете.

Рисунок 14 – Зависимость U_У.И(t), найденная операторным методом

Зависимости переменных ЭМС, определенные с помощью преобразований Лапласа, полностью совпали с аналогичными зависимостями, найденными классическим методом.

9. Использование обратного преобразования Лапласа с ненулевыми начальными условиями для нахождения аналитической функции, описывающего переходный процесс реверса ненагруженной ЭМС с номинальной частотой вращения ДПТ НВ

Ненулевые начальные условия:

i(100)=0, так как ведется расчет для ненагруженной ЭМС;

ω(100)=-ω_н=-270,681 рад/с;

U_У.И.(100)=- U_ЗАД=-10В

Система дифференциальных уравнений в каноническом виде:

Применяя прямое преобразование Лапласа при нулевых начальных условиях, получаем систему линейных алгебраических уравнений (СЛАУ):

Представим СЛАУ в виде А(р)х(р)=В(р):

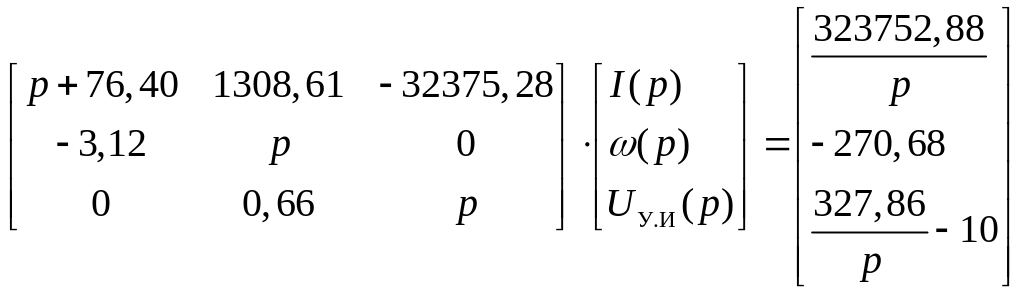
Решим СЛАУ методом Крамера:

Изображения функций:

Применяем обратное преобразование Лапласа, для нахождения оригиналов функции, описывающих переходный процесс реверса ненагруженной ЭМС:

После нахождения оригиналов, строим полученные функции

Рисунок 15 – Зависимость тока от времени при реверсе ненагруженной ЭМС

Рисунок 16 – Зависимость скорости от времени при реверсе ненагруженной ЭМС

Рисунок 17 – Зависимость напряжения управления от времени при реверсе ненагруженной ЭМС