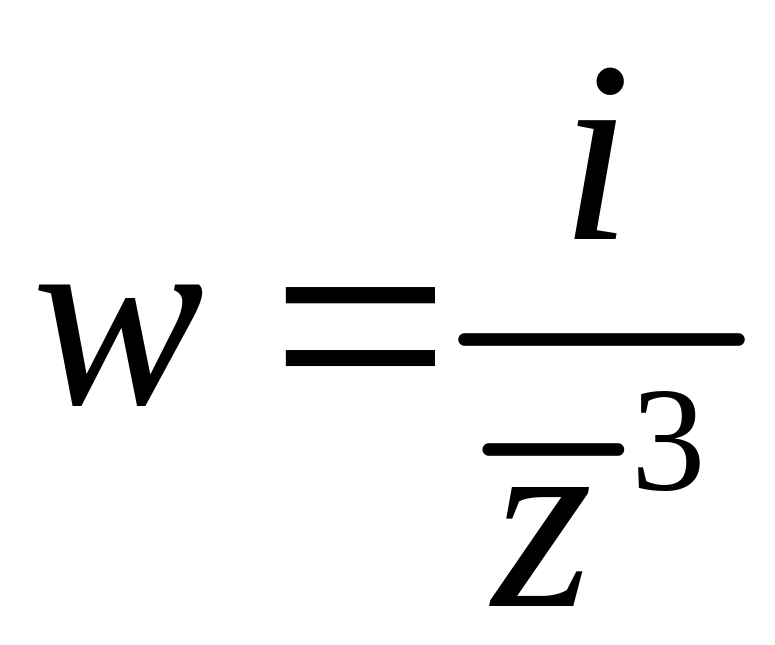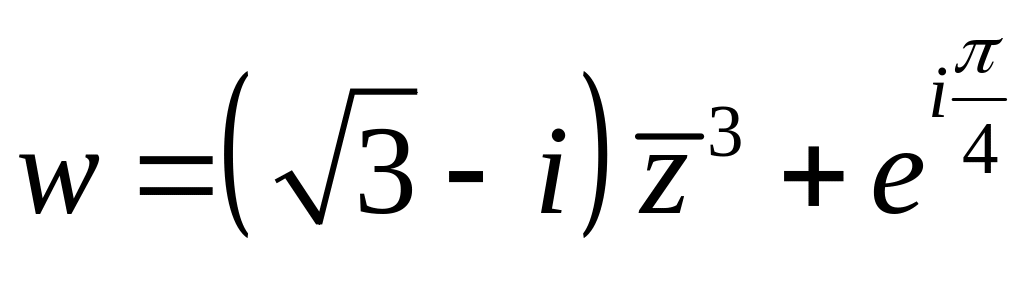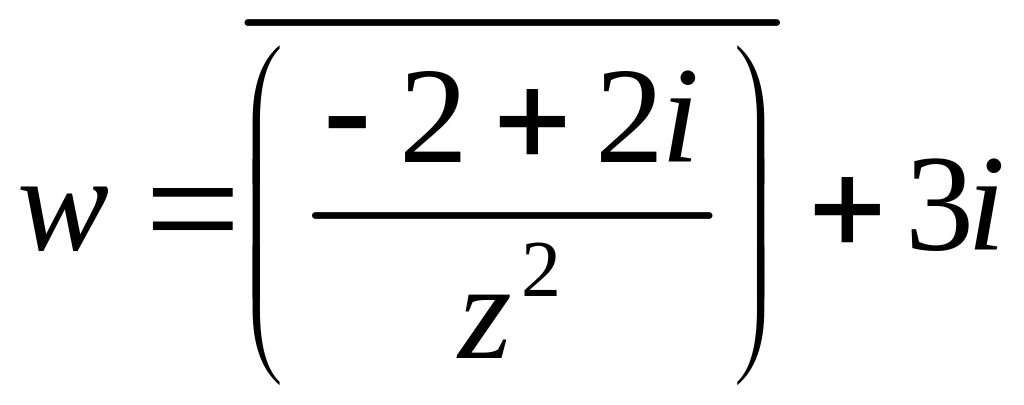Задание №5.
Знайти та зобразити область, в яку функцiя w=f(z) переводить закреслену область.
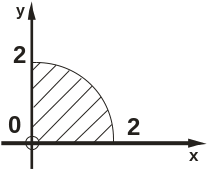
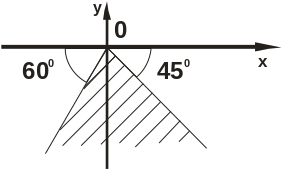
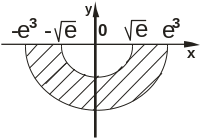
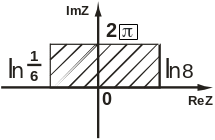
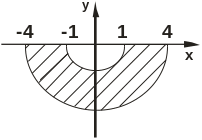
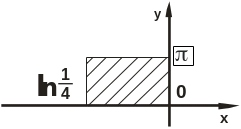
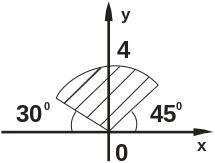
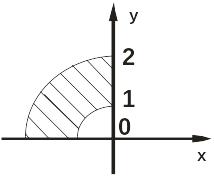
Завдання № 6.
З’ясувати, при яких заданi функцiї диференцiйовнi, i знайти їх похiднi в цих точках.
Лiтература
Бугров Я.С., Никольский С.М. Дифференциальные уравнения, кратные интегралы, ряды, функции комплексного переменного. М.: “Наука”, 1989, 464 с.
Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций комплексного переменного. М., 1970.
Гольдберг А. А. та iн. Комплексний аналiз. Львiв, Афiша, 2002, 203 с.
Маркушевич А. И., Маркушевич Л. А. Введение в теорию аналитических функций. М.: Просвещение, 1977, 320 с.
Методические указания и задания к типовому расчету «Элементы теории функций комплексного переменного». Давыдов Р. Н., Храбустовский В. Н., Х., ХИИТ, 1993, 30 с.
Мышкис А. Д. Лекции по высшей математике. М., “Наука”, 1969, 640 с.
Сборник задач по теории аналитических функций / Под. ред. М. А. Евграфова. М., 1972.
Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. М.:Наука, 1979, 304 с.
Эйдерман В. Я. Основы теории функций комплексного переменного и операционного исчисления. М., Физматлит, 2002, 256 с.