З рис. 6 знаходимо, що

Тодi i знаходять з урахуванням чвертi, в якiй мiститься кут .

Пiдставивши (1.1) до , одержуємо тригонометричну форму комплексного числа

, де , а .

Позначимо

Ця формула зветься формулою Ейлера. Тодi комплексне число можна записати у показниковiй формi

.

Приклад 6.

Зобразити множину всiх точок комплексної площини, якi задовольняють умовi .

Розв’язок.

Зауважимо, що дорiвнює вiдстанi мiж точками i : Тому умова задає кiльце з центром у точцi z₀=1 i радiусами та (див. рис. 7).

Рис. 7.

Приклад 7.

Зобразити множину всiх точок комплексної площини, що задовольняють нерiвностям

Розв’язок.

Рис. 8.

Приклад 8.

Записати в показниковiй формi .

Розв’язок.

Зобразимо комплексне число на площинi

Рис. 9.

З рис. 9 знайдемо , а дорiвнює 3. Отже .

Приклад 9.

Записати комплексне число в тригонометричнiй та показниковiй формi.

Розв’язок.

,

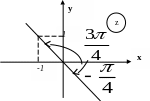
Рис. 10.

В тригонометричнiй формi комплексне число має вигляд

,

а в показниковiй

Дiї над комплексними числами в тригонометричнiй або показниковiй формi

При множеннi (дiленнi) комплексних чисел їх модулi множаться (дiляться), а аргументи додаються (вiднiмаються).

Якщо , , то , .

Наслiдок.

Формула Муавра

.

Приклад 10.

Записати в алгебраїчнiй формi , якщо

Розв’язок.

.

Приклад 11.

Записати в алгебраїчнiй формi , якщо .

Розв’язок.

.

Приклад 12.

Записати в алгебраїчнiй формi .

Розв’язок.

Запишемо комплексне число у показниковiй формi.

Модуль дорiвнює

Рис. 11.

.

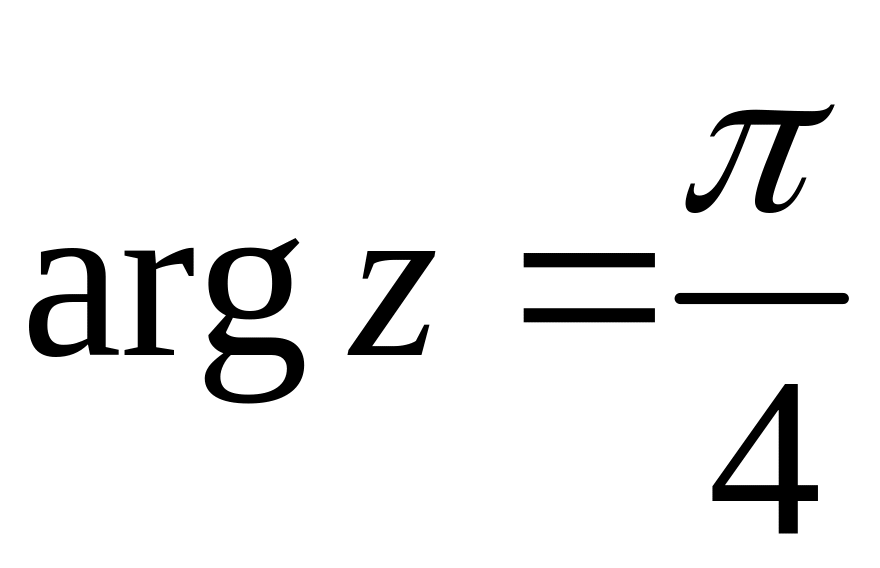Комплексне число у показниковiй формi має вигляд

.

За формулою Муавра

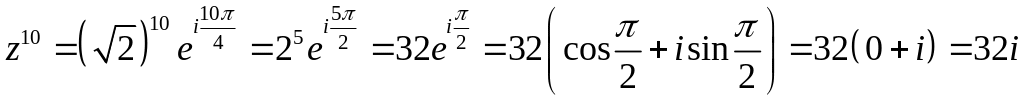
Приклад 13.

Записати в алгебраїчнiй формi .

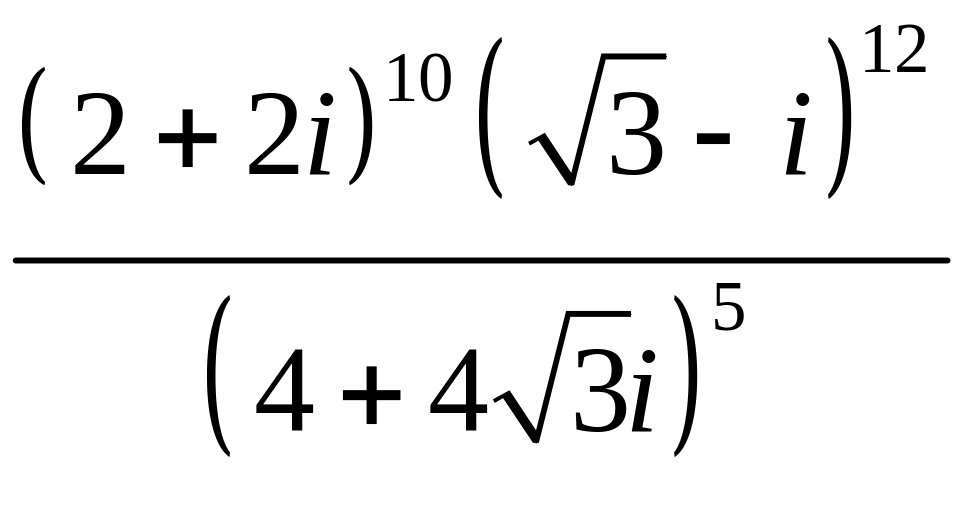Розв’язок.

Позначимо , , .

З апишемо цi комплекснi числа в показниковiй формi. Якщо , то , а головний аргумент знайдемо з рис. 12.

Рис. 12.

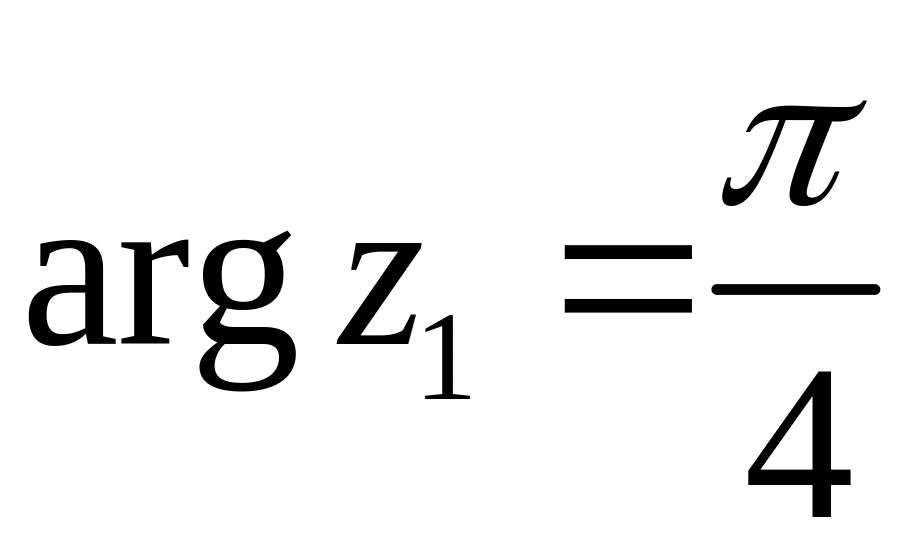, тодi .

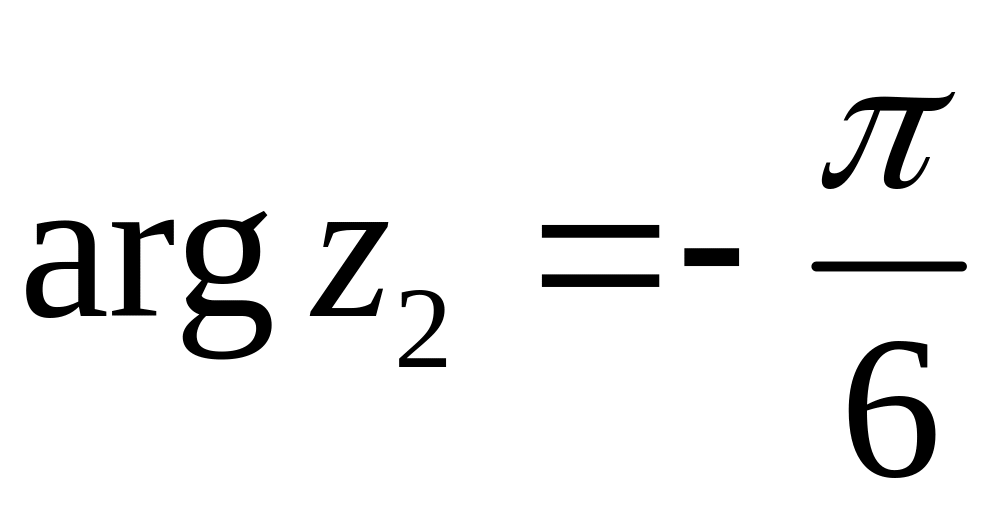Якщо , то , а , де – кут у IV чвертi, тодi (див. рис. 13)

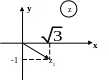
Рис. 13.

, тодi , а головне значення аргументу

, – кут I чвертi,

Рис. 14.

Основнi елементарнi функцiї комлексної змiнної

1. Окремі випадки лінійної функції

а. Функцiя здiйснює зсув фiгури на вектор з координатами

Приклад 14.

Функцiя зсуває пiвплощину на вектор (0,1)

Рис. 15. Рис. 16.

б. Функцiя .

Якщо , то функцiя усi фiгури розтягує у раз та повертає на кут навколо початку координат проти годинникової стрiлки.

Приклад 15.

Функція повертає будь-яку фiгуру (див. рис. 17) на кут (див. рис. 18).

v

u

Рис. 17. Рис. 18.

2. Окремі випадки степеневої функції з цілим показником

а. Функція

Приклад 16.

Функція відображує першу чверть у верхню півплощину (див. рис. 19 та 20).

Рис. 19. Рис. 20.

Якщо перейти до показникової форми , то .

б. Функція

Запишемо в показниковiй формi , тодi 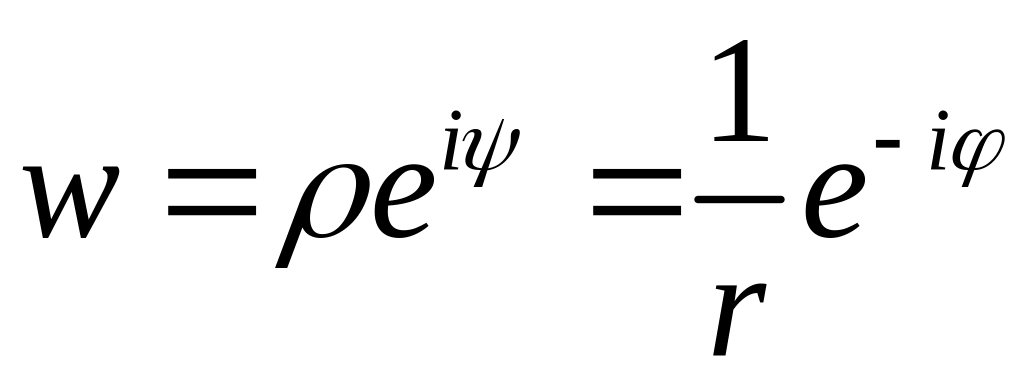, тобто

3. Корень степенi n з комплексного числа z.

Коренєм степенi n з комплексного числа z називається таке комплексне число , що задовольняє рiвностi .

Для натурального iснує рiвно рiзних коренiв, якi знаходяться за формулою

.

Коренi степенi з комплексного числа знаходяться у вершинах правильного кутника, вписаного у коло з центром у точцi О(0,0) та радiуса .

Приклад 17.

Знайти всi значення .

Розв’язок.

Щоб обчислити корiнь з комплексного числа, треба записати це число у показниковiй формi

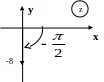
Рис. 21.

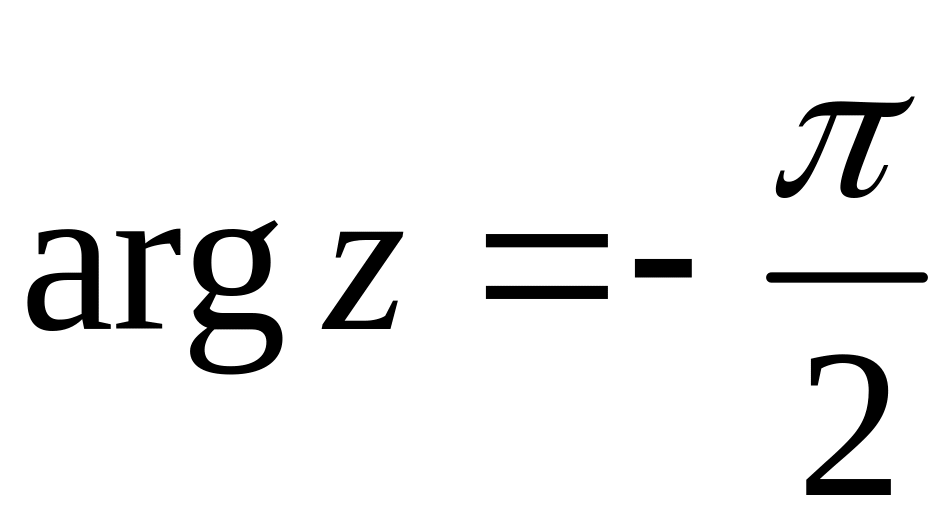(див. рис. 21), .

.

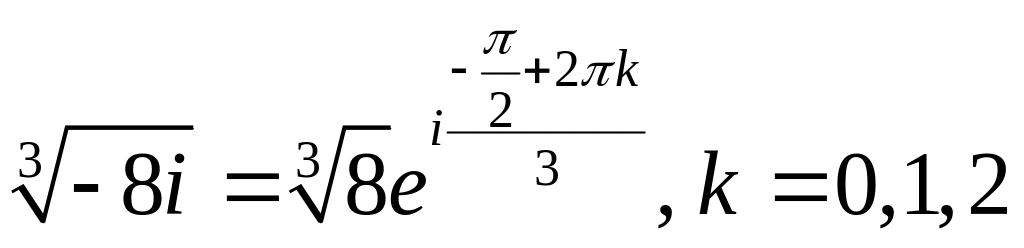При , отримаємо

,

, ,

, .

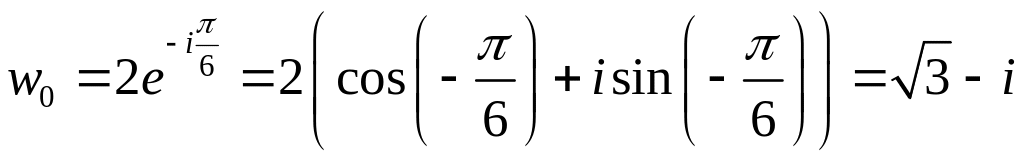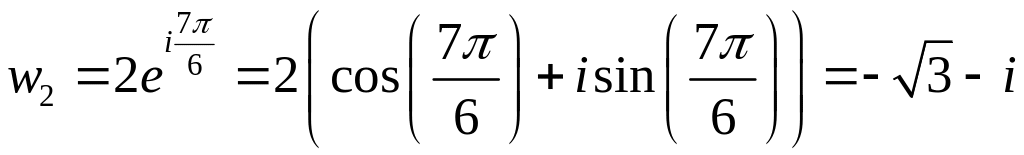Зобразимо коренi третьої степенi з на площинi. Коренi знаходяться у вершинах правильного трикутника, вписаного в коло радiуса 2 та центром у нулi (див. рис. 22).

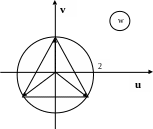
Рис. 22.

Приклад 18.

Знайти всi значення .

Розв’язок.

Запишемо комплексне число в показниковiй формi

,

,

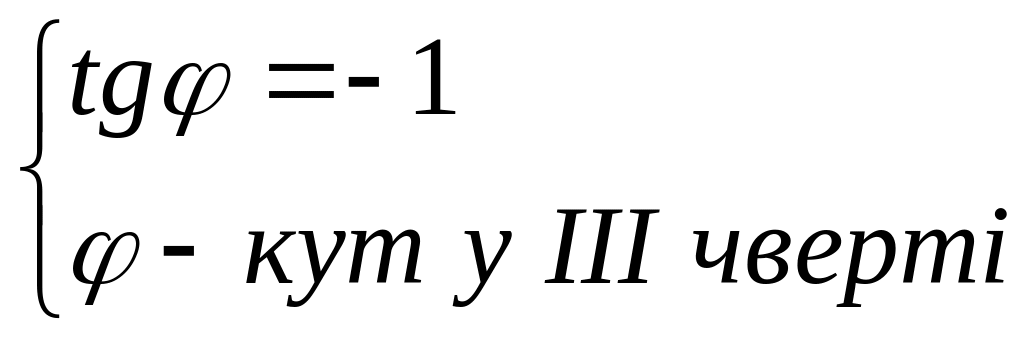
Тодi коренi з комплексного числа мають вигляд

.

,

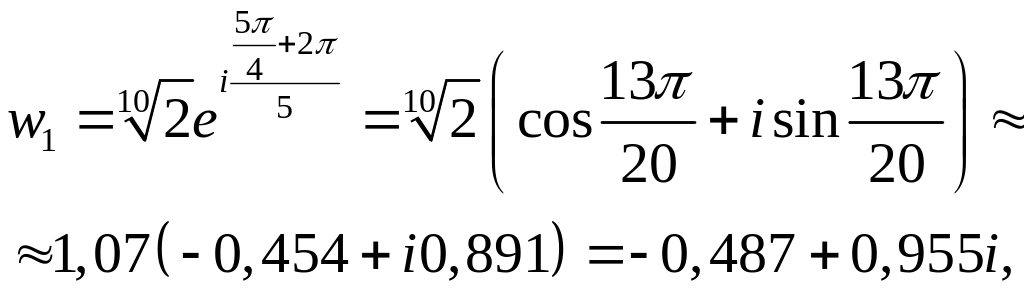
Зобразимо коренi на малюнку

Рис. 23.

4. Показникова функцiя

.

Показникова функцiя має чисто уявний перiод

Функцiя прямi, що параллельнi дiйснiй осi переводить у променi, якi виходять з початку координат, а прямi, що параллельнi уявнiй осi переводить у кола з центром у початку координат.

,

Приклад 19.

Рис. 24. Рис. 25.

5. Гiперболiчнi функцiї

, , , .

Приклад 20.

Записати в алгебраїчнiй формi .

Розв’язок.

.

6. Тригонометричнi функцiї

, , , .

Між тригонометричними та гіперболічними функціями існують наступні співвідношення:

.

7. Логарифмiчною функцiєю називається функцiя, обернена до показникової, тобто функцiя така, що , . Логарифмiчна функцiя має нескiнченно багато значень (функція має період ). Вони дорiвнюють

,

де називається головним значенням логарифмічної функції.

.

Функцiя прямi, що параллельнi дiйснiй осi переводить у кола з центром у початку координат, а прямi, що параллельнi уявнiй осi переводить у променi, якi виходять з початку координат.

Приклад 21.

Функція переводить область з рис. 26 у півполосу (див. рис. 27).

Рис. 26. Рис. 27.

8. Загальна степенева функцiя комплексної змiнної визначається за допомогою показникової та логарифмiчної функцiї наступним чином:

Приклад 22.

Записати в алгебраїчнiй формi .

Розв’язок.

Позначимо . Тодi , , ,

.
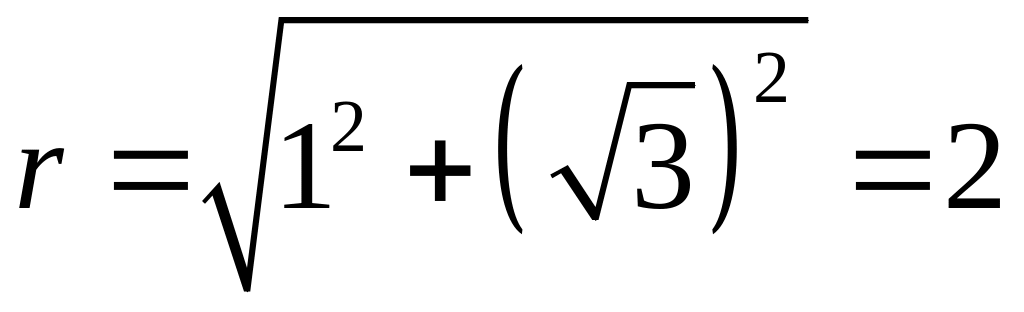
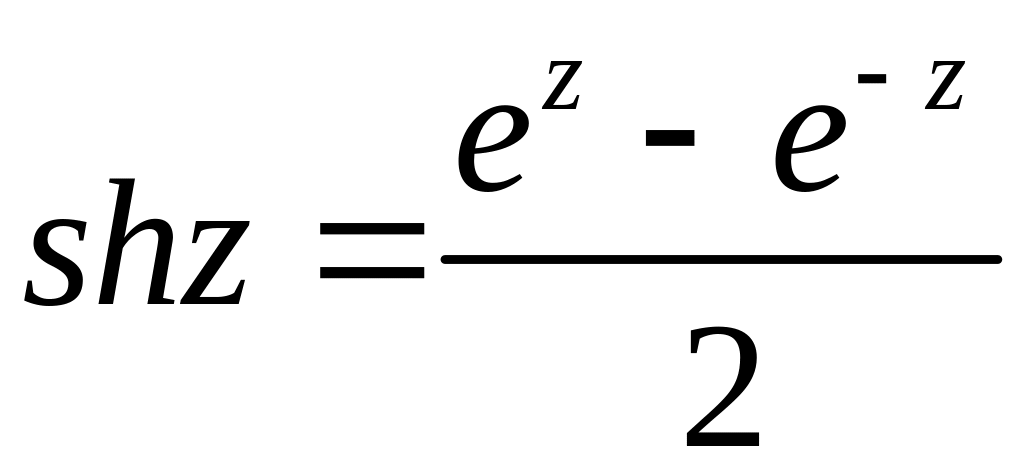