УКРАїнська державна академія

залізничного транспорту

ФАКУЛЬТЕТ УПП

Кафедра “Вища математика”

теорiЯ ФУНКЦІЙ комплексної змiнної

частина 1

МЕТОДИЧНІ ВКАЗІВКИ І ЗАВДАННЯ

до розрахунково-графічної роботи

з розділу дисципліни

“ВИЩА МАТЕМАТИКА”

Харків – 2006

Методичні вказівки розглянуто і рекомендовано до друку на засіданні кафедри вищої математики УкрДАЗТ, протокол № від 2006 р.

Методичні вказівки призначені для студентів денної форми навчання загальнотехнiчних спеціальностей.

Укладачі:

доц. Храбустовський В. І.,

доц. Осмаєв О. А.,

доц. Удодова О. I.

Рецензент

проф. Куліш Ю. В.

ВСТУП

Методичні вказівки присвячені розділу курсу вищої математики: комплекснi числа та елементарні функції комплексної змінної. Вони містять теоретичні відомості, зразки розв'язання задач з розгорнутими поясненнями, варіанти завданнь для виконання РГР або домашніх завдань, список учбової літератури.

Методичні вказівки рекомендовані для студентів загальнотехнiчних спецiальностей денної форми навчання спеціальностей АіТ та ТСМ а також деяких інших, зокрема ЕТ та ЕСК. Вони призначені для виконання розрахунково-графічної роботи або індивідуальних домашніх завдань.

Номери варіантів індивідуальних завдань або розрахунково-графічних робіт видаються викладачем.

Теоретичнi поняття

КОМПЛЕКСНI ЧИСЛА ТА ДIЇ З НИМИ

Поняття комплексного числа

Комплексним числом називається вираз виду

,

де – дiйснi числа ( ), а  – уявна одиниця, яка визначається умовою . Множина комплексних чисел позначається .

Запис комплексного числа у виглядi , називається алгебраїчною формою комплексного числа . При цьому зветься дiйною частиною комплексного числа i позначається , а – уявною частиною комплексного числа , i позначається .

Дiйснi числа є окремим випадком комплексних чисел, а саме, це комплекснi числа, у яких уявна частина дорiвнює нулю

.

Комплексне число, у якого дiйсна частина дорiвнює нулю, називається уявним числом

Геометричне тлумачення комплексного числа Комплексне число зображають геометрично вектором або точкою на площинi , яка в цьому випадку зветься комплексною (див. Рис. 1).

Рис. 1.

Спряженим до комплексного числа зветься комплексне число

.

Комплекснi числа та розташованi на комплекснiй площинi симетрично вiдповiдно дiйсної осi (див. рис. 2).

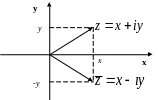
Рис. 2.

Приклад 1.

Зобразити множину всiх точок комплексної площини, якi задовольняють умовi .

Розв’язок.

Оскiльки , то . Зображуємо множину (див. рис. 3).

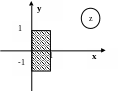
Рис. 3.

Дiї з комплексними числами в алгебраїчнiй формi

1. Додавання комплексних чисел. Для того щоб додати комплекснi числа, треба вiдповiдно додати їх дiйснi та уявнi частини.

Приклад 2.

Знайти , якщо ,

Розв’язок.

Зауважимо, що при додаваннi комплексних чисел вiдповiднi вектори додаються (див. рис. 4).

Рис. 4.

2. Добуток комплексних чисел, що представлені в алгебраїчній формі, обчислюється за звичайними правилами алгебри з урахуванням того, що

Приклад 3.

Знайти , якщо , .

Розв’язок.

3. Дiлення двох комплексних чисел. Для знаходження частки комплексних чисел потрiбно чисельник та знаменник домножити на число спряжене до знаменника.

Приклад 4.

Записати в алгебраїчнiй формi

Розв’язок.

Приклад 5.

Зобразити криву на комплекснiй площинi, яка задається рiвнянням

.

Розв’язок.

,

,

,

,

.

О тримали коло з центром у точцi О(0,0) та радiуса 2 (див. рис. 5).

Рис. 5.

Тригонометрична I показникова форма комплексного числа

Для геометричного тлумачення множення i дiлення комплексних чисел введемо на комплекснiй площинi полярнi координати (див. рис. 6).

Число називають модулем комплексного числа .

Аргументом комплексного числа називають кут який утворює вектор з додатнiм напрямком осi Ох. (При цьому вважається, що кут ( ), якщо кут відраховується від вказаного напрямку проти (за) годинниковою стрілкою) Аргумент комплексного числа визначається з точнiстю до цiлого числа повних обертiв. Значення аргументу, якi задовольняють умовi (або ) звуться головним значенням аргументу i позначаються .

.

Аргумент числа не визначений, а його модуль дорiвнює нулю.

Рис. 6.