6. Приклади розв’язання завдань контрольної роботи з дисципліни

Контрольна робота являє собою вирішення комплексу задач за основними темами дисципліни:

„Зведення та групування статистичних даних” – завдання 1;

„Ряди розподілу” – завдання 2;

„Ряди розподілу” – завдання 3;

„Ряди динаміки” завдання 4;

„Індекси” – завдання 5 і 6;

„Вибіркове спостереження” – завдання 7;

В даному розділі наведені приклади вирішення усіх 7 завдань контрольної роботи з дисципліни, які допоможуть студентами уникнути помилок при виконанні контрольної роботи.

Завдання 1

За наведеними даними про обсяг капіталу та прибуток комерційних банків скласти аналітичне групування, що відображає залежність прибутку банків від суми капіталу, створивши 3 групи з рівним інтервалом обсягу капіталу.

Розв’язання

Комерційні банки за розміром капіталу та прибутку

Номер банку	Обсяг капіталу, млн.грн.	Прибуток банку, млн.грн.
1	6,2	4,6
2	11,9	8,5
3	7,6	5,3
4	10,5	8,8
5	3,0	2,2
6	5,2	4,3

Продовження таблиці

7	7,3	6,0
8	4,4	3,0
9	8,3	5,8
10	5,2	3,3
11	12,0	8,2
12	5,1	3,6

Застосувавши рівні інтервали, визначимо їх ширину і сформуємо інтервали.

Для обсягу капіталу:

h	=	Xmax - Xmin	=	12,0-3,0	=	3,0 млн.грн.
		n		3

Інтервали: 3-6; 6-9; 9-12.

Для підтвердження наявності зв’язку між обсягом капіталу (факторна ознака) та прибутком (результативна ознака) використовуємо аналітичне групування.

Аналітичне групування банків за обсягом капіталу і прибутку.

Групи за обсягом капіталу, млн.грн.	Кількість банків	Обсяг капіталу, млн.грн.	Прибуток, млн.грн
			Разом	В середньому на один банк
3-6	5	22,9	16,4	3,28
6-9	4	29,4	21,7	5,43
9-12	3	34,4	25,5	8,5
Всього	12	86,7	63,6	х
В середньому	х	х	х	5,3

Дані таблиці свідчать про прямий зв’язок між ознаками. При збільшенні обсягу капіталу різниця між групами по прибутку на один банк зростає, що характеризує збільшення впливу факторної ознаки (обсягу капіталу) на результативну ознаку (прибуток).

Для другої групи: 5,43 – 3,28 = 2,15 млн.грн.;

Для третьої групи: 8,50 – 5,43 = 3,07 млн.грн.

Завдання 2

Визначити середній стаж працівника, розмах варіації, середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.

Вихідні дані:

№ з/п	Стаж роботи	Кількість працівників
1	До 4-х	15
2	4-8	18
3	8-12	24
4	12-16	30
5	16-20	20

Розв’язання

Розмах варіації – це різниця між середніми значеннями останнього і першого інтервалів

R = X_max – X_min = 18 – 2 = 16

Розрахунок інших показників варіації наведений в таблиці:

				( )	( )2	( )2 .
2	15	30	-9	125	81	1215
6	18	108	-5	90	25	450
10	24	240	-1	24	1	24
14	30	420	3	90	9	270
18	20	360	7	140	49	980
всього	107	1158	х	479	х	2939

Середній стаж працівника

	=	1158	=	11 років
		107

Обчислюємо показники варіації

• середнє лінійне відхилення

d	=	∑ ( )	=	479	=	4,5 року
		∑		107

• дисперсія

σ2	=	∑ ( )2 .	=	2939	=	27,5
		∑		107

• середнє квадратичне відхилення

σ = = = 5,2 роки

- коефіцієнт варіації

Vσ	=	σ	=	5,2	·	100	=	47,3%
				11

Показники варіації дозволяють дати оцінку відхилення варіації від середньої.

Значення коефіцієнту варіації (47,3 %) свідчить про те, що розглянута сукупність

кількісно неоднорідна, тому що Vσ > 33,0 %.

Завдання 3

Розрахунок групових, між групової та загальної дисперсії показано в таблиці, на прикладі урожайності винограду.

Сорт винограду	Кількість кутів, fі	Урожайність з одного куша, кг у	∑у
Аліготе	5	2,3; 2,2; 2,7; 2,6; 2,2	12	2,4
Фетяска	8	2,9; 3,3; 2,7; 2,8; 3,2; 3,4; 2,8; 2,9.	24	3,0
Рислінг	7	3,6; 4,0; 4,1; 4,4; 3,8; 3,9; 4,2.	28	4,0
В цілому	20	х	64	3,2

Варіація урожайності окремо для кожного сорту винограду визначається трьома внутрішньогруповими дисперсіями. Для сорту винограду „Аліготе” внутрішньогрупова дисперсія становить:

Аналогічно обчислені внутрішньогрупові дисперсії для сорту винограду „Фетяска” та „Рислінг” становлять:

; .

Середне з групових дисперсій дорівнює

Міжгрупова дисперсія становить

де

Загальну дисперсію урожайності визначимо за правилом складання дисперсій як суму середньої з групових та міжгрупової дисперсії:

Загальну дисперсію можна визначити і безпосередньо за формулою

дає такий самий результат .

Завдання 4

Є такі дані про виробництво продукції в Україні:

Роки	2002	2003	2004	2005	2006
Виробництво продукції, тис.т	1621	1947	2109	2247	2486

Визначити:

1. Ланцюгові та базисні показники динаміки: абсолютний приріст; темп зростання; темп приросту; абсолютне значення 1 % приросту.

2. Середній рівень ряду за 5 років;

3. Середньорічний темп зростання і приросту;

4. Середньорічний абсолютний приріст.

Розв’язання

На основі вихідних даних складається розрахункова таблиця:

Роки	В ипуск продукції, тис.т	Абсолютний приріст, тис.грн.		Темп зростання		Темп приросту		Абсолютне значення 1 % приросту
		ланцюговий	базисний	ланцюговий	базисний	ланцюговий	базисний	ланцюговий	базисний
2002	1621				1,000
2003	1947	326	326	1,201	2,201	20,1	20,1	16,2	16,2
2004	2109	162	488	1,083	1,301	8,3	30,1	19,5	16,2
2005	2247	138	626	1,065	1,386	6,5	38,6	21,2	16,2
2006	2486	239	865	1,106	1,534	10,6	53,4	22,5	16,2

1. Середній рівень виробництва продукції – середня арифметична проста

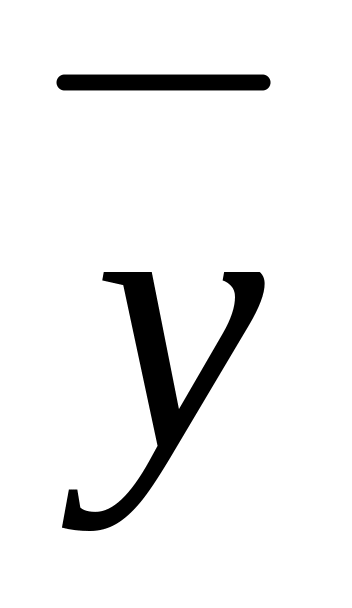
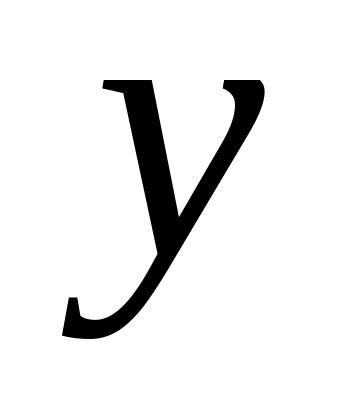	=	∑ і	=	1621+1947+2109+2247+2486	=	10410:5=2082 тис.т.
		k		5

2. Середній абсолютний приріст

	=	n– 0	=	2486-1621	=	865	=	216,25 тис.т.
		n-1		4		4

3. Середній темп зростання за період 2002…2006 рр.:

=

=

=

=

1,1128 або 111, 28%

4. Середній темп приросту

= (%) – 100 =

= 111,28 – 100 = 11,28%

Висновок: 1. Середній рівень виробництв становить 2082 тис. т.

2. Середній абсолютний приріст становить 216, 25 тис. т.

3. Випуск продукції щорічно зростає на 11,28 % або на 216,25 тис. т.

Завдання 5

Є такі дані про реалізацію кондитерських виробів:

Назва продукції	Реалізовано, тонн		Оптова ціна за 1 т, грн.
	липень	серпень	липень	серпень
1. Біла акація	250	270	14800	15155
2. Білочка	204	210	15800	16910

Визначити:

1) індивідуальні індекси цін та фізичного обсягу реалізації;

2) агрегатні індекси фізичного обсягу продукції, цін, вартості продукції;

3) абсолютний приріст продукції в т.ч. за рахунок зміни фізичного обсягу реалізації та оптових цін.

Розв’язання

1. Складається така розрахункова таблиця:

Назва продукції	Реалізовано, тонн		ig	Ціни за 1 т., грн.		ip	Вартість реалізованої продукції, тис.грн.
	у липні	у серпні		у липні	у серпні
	g0	g1		p0	p1		p1 g1	p0 g1	p0 g0
Біла акація	250	270	1,080	14800	15155	1,0240	4091,9	3996	3700
Білочка	204	210	1,0294	15800	16910	1,0703	3551,1	3318	3223
Всього	-	-	-	-	-	-	7643	7314	6923

2. Агрегатний індекс фізичного обсягу

Ig	=	∑ p0 g1
		∑ p0 g0

Ig	=	7314	=	1,0565
		6923

3. Агрегатний індекс цін

Ip		=		∑ p1 g1
				∑ p0 g1
Ip	=		7643		=		1,045
			7314

4. Агрегатний індекс вартості продукції

Ipg	=	Ip · Ig	=	∑ p1 g1	·	∑ p0 g1	=	∑ p1 g1
				∑ p0 g1		∑ p0 g0		∑ p0 g0

Ipg	=	7643	=	1,104
		6923

або I_pg = 1,045 · 1,0565 = 1,104

5. Загальний приріст реалізації

7643 – 6923 = 720 тис.грн.

в т.ч.: за рахунок зміни цін

7643 – 7314 = 329 тис.грн.

за рахунок зміни фізичного обсягу

7314 – 6923 = 391 тис. грн. 329 + 391 = 720 тис.грн.

Завдання 6

Є такі дані про роботу цехів кондитерської фабрики за два періоди:

Цехи	Випуск продукції, тис.грн.		Витрати праці, люд.-год.
	Базисний період	Звітний період	Базисний період	Звітний період
Карамельний	109,2	163,5	2100	2850
Мармеладний	35,0	38,9	1000	1050

Визначити у звітному періоді у порівнянні з базисним:

а) зміну продуктивності праці по карамельному цеху і по мармеладному це ху;

б) зміну продуктивності праці по обох цехах разом (індекс змінного складу)

в) зважений індекс продуктивності праці (індекс постійного складу)

г) індекс структурних зрушень (пояснити його зміст).

Розв’язання

Цехи	Випуск продукції, тис.грн.		Витрати праці, люд-год.		Продуктивність праці, грн/люд.-год.		IW
	в базисному періоді	в звітному періоді	в базисному періоді	в звітному періоді	в базисному періоді	в звітному періоді
	Q0=W0·T0	Q1=W1·T1	T0	T1	W0	W1
Карамельний	109,2	165,3	2100	2850	52	58	1,1154
Мармеладний	35,0	38,9	1000	1050	35	37	1,0571
Всього	144,2	204,2	3100	3900	х	х	х

1. Зміна продуктивності праці по карамельному цеху (індивідуальний індекс)

іwк	=	W1к	=	58	=	1,1154 тобто 111,54 %
		W0к		52

2. Зміна продуктивності праці по мармеладному цеху (індивідуальний індекс)

іwм	=	W1м	=	37	=	1,0571 тобто 105,71 %
		W0м		35

3. Зміна продуктивності праці по обох цехах разом (загальний індекс змінного складу)

Iwзс

=

W1: W0

=

∑ W1 T1

:

∑ W0 T0

=

204,2

:

144,2

=

52,36:46,52=1,1255.

∑T1

∑T0

3900

3100

Продуктивність праці по обох цехах зросла на 12,6 %, тобто загальний індекс змінного складу вийшов за межі індивідуальних індексів, які він узагальнює.

Отже, I_w є більшим найбільшого з індивідуальних індексів 1,1255 >1,1154. Це явище статистичного парадоксу.

4. Індекс продуктивності праці фіксованого складу I_w^фс

Iwфс

=

W1: W0

=

∑ W1 T1

:

∑ W0 T1

=

204,2

:

184,95

=

52,36:47,42=1,1042.

∑T1

∑T1

3900

3900

Отже, продуктивність праці за рахунок зміни самого показника (індексованої величини) зросла на 10,42 %.

6. Індекс структурних зрушень I_w^зс показує зміну продуктивності праці за рахунок зміни у структурі продукції.

Оскільки I_w^зс = I_w^фс · I_w^сз , то I_w^сз = I_w^зс : I_w^фс

I_w^сз = 1,1255 : 1,1042 = 1,0193 або 101,9 %

Структура продукції покращилась у зв’язку зі збільшенням частки менш трудомісткої продукції – карамелі:

(109,2 : 144,2) · 100 = 75,7 %, (165,3 : 204,2) · 100 = 81 %.

Завдання 7

На хлібоприймальному підприємстві формують партії зерна для подальшого його сушіння. Для установлення режиму роботи зерносушарки необхідно знати вологість зерна, яка була установлена впродовж дня взяттям вибірково 10 проб з автомашин із зерном.

Номер проби	1	2	3	4	5	6	7	8	9	10
Вологість зер- на, %	18,4	17,8	18,0	17,5	17,7	18,8	19,0	17,9	18,6	18,7

Визначити:

1. Середню вологість зерна пшениці за вибірковою сукупністю.

2. Середню та граничну помилки вибіркової середньої.

3. Межі, в яких з ймовірністю 0,95 перебуває середня вологість зерна у генеральній сукупності.

Зробити висновки.

Розв’язання

Для знаходження середньої вологості зерна та дисперсії вибіркової сукупності складаємо допоміжну таблицю:

		–	( – )2
1	18,4	0,16	0,026
2	17,8	-0,44	0,194
3	18,0	-0,24	0,058
4	17,5	-0,74	0,547
5	17,7	-0,54	0,292
6	18,8	-0,56	0,314
7	19,0	0,76	0,577
8	17,9	-0,34	0,115
9	18,6	0,36	0,130
10	18,7	0,46	0,211
Разом	182,4	х	2,274

1. Середнє значення вологості зерна пшениці за даними таблиці

За даними таблиці розраховуємо вибіркову дисперсію

2. Середня квадратична помилка вибірки дорівнює

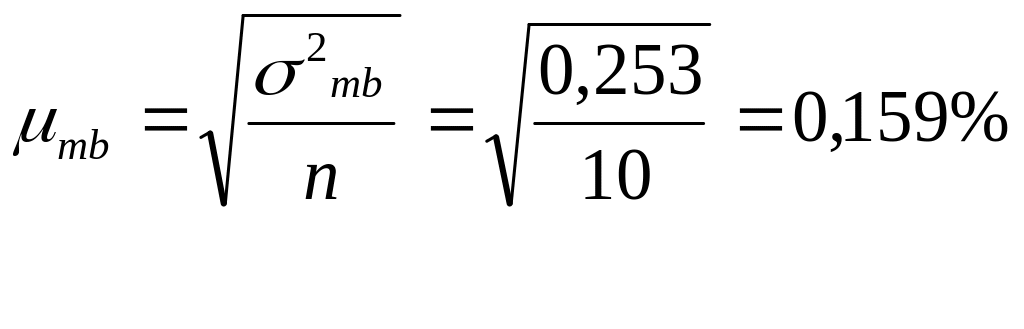
Отже, вибіркова середня = 18,24 % є оцінкою генеральної середньої з середньою помилкою

При заданому рівні ймовірності p = 0,95 коефіцієнт довіри t при малій вибірці може бути визначено з використанням математичних таблиць розподілу Стюдента, які є в навчальній літературі:

t = 2,26 при рівні значущості λ = 0,05 та числі ступенів вологості к = n-1=10-1=9

тоді гранична помилка вибірки дорівнює

3. Установимо інтервальну оцінку середньої вологості зерна пшениці в генеральній сукупності:

,

18,24 – 0,36 ≤ ≤18,24+0,36,

17,88≤ ≤ 18,60.

Таким чином, з ймовірністю 0,95 можна стверджувати, що середня вологість зерна в генеральній сукупності перебуває в інтервалі від 17,88 % до 18,60 %.

Список використаної літератури.

Зміст