4. Динамика

Предмет динамики

Динамика – раздел механики, посвящённый изучению движения материальных тел с учётом причин их вызывающих.

Масса. Инерция

Под инерцией (от лат. inertia  — бездеятельность, косность)  понимают свойство тела сохранять состояние своего движения или покоя (в инерциальной системе отсчёта), когда внешние воздействия на тело отсутствуют или взаимно уравновешиваются, и изменять эти состояния тем медленнее, когда внешние воздействия не уравновешиваются.

Инертность у различных тел проявляется в разной степени. Мерой инертности тел является масса.

Масса m – cкалярная физическая величина, являющаяся мерой инерции (во втором законе Ньютона: = , гравитации (в законе всемирного тяготения: F_г = ) и энергии (в законе взаимосвязи массы и энергии: E = mc²).

В СИ: [m] = кг⁵ .

В релятивистском случае ( ) справедливо следующее:

m = ,

где m₀ – масса покоя (m> m₀).

Плотность тела – масса единицы объёма тела: = , ( ).

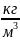Сила

Сила - это векторная величина, являющаяся мерой механического воздействия на рассматриваемое тело со стороны других тел или полей.

В СИ: [F] = Н⁶ (ньютон).

В результате действия силы тело изменяет свою скорость, либо деформируется.

Силы бывают внешние и внутренние.

Внешние силы – силы, действующие на систему стороны внешних тел.

Внутренние силы – это силы взаимодействия между частями рассматриваемой системы.

Механическая система тел называется замкнутой (изолированной), если она не взаимодействует с внешними телами, т.е. на неё внешние силы не действуют ( _внешн.= 0).

Понятие изолированной системы – это идеализация, т.е. таких систем реально не существует.

Различают так же силы консервативные и неконсервативные.

Консервативной (потенциальной) силой называется сила, работа которой зависит только от начального и конечного положения точки её приложения и не зависит от вида её траектории (например, консервативные силы: сила тяжести, сила упругости, кулоновская (электростатическая) сила).

Остальные силы – неконсервативные.

Неконсервативные силы подразделяются на диссипативные⁷ и гироскопические.

Диссипативные силы – силы, полная работа которых отрицательная (например: сила трения, сила сопротивления).

Гироскопические силы – силы, зависящие от скорости тела и действующие перпендикулярно этой скорости (например: центростремительные силы; сила Лоренца, действующая со стороны магнитного поля, на движущийся в этом поле электрический заряд).

Гироскопические силы энергию тела не изменяют и работы не совершают.

Сложение сил – нахождение геометрической суммы (т.н. главного вектора) данной системы сил путем последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая (рис. 28).

Рис. 28.

Пример.

Если к телу приложены две силы в одной точке, то равнодействующая этих сил равна: (рис. 29).

Рис. 29.

Модуль равнодействующей двух сил можно определить по теореме косинусов:

R =

или при = 90°— по теореме Пифагора.

Примеры сил в механике

1). Сила гравитации (закон всемирного тяготения)

Исторический очерк

Сама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие.

Рис. 30. Исаак Ньютон⁸. Без преувеличения один из величайших научных умов за всю историю человечества. Именно Ньютону мы обязаны той картиной физического мира, которая сложилась к сегодняшнему дню.

Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера). В своём основном труде «Математические начала натуральной философии» (1687) Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Теория Ньютона, в отличие от гипотез предшественников, имела ряд существенных отличий. Ньютон опубликовал не просто предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель.