Кинематика вращательного движения
Понятие о вращательном движении
Различают четыре типа вращения: вращение вокруг неподвижной оси, вращение вокруг свободных осей, движение с одной неподвижной точкой (гироскоп), плоское движение (поступательное движение с полюсом + вращение вокруг этого полюса, например, шар или цилиндр, катящиеся по плоской поверхности).
Будем рассматривать только вращение тела вокруг неподвижной оси (см. рис. 23).
Вращательное движение вокруг неподвижной оси – это движение твёрдого тела, при котором какие-либо две его точки (т.О и т.О1) остаются всё время неподвижными.
Прямая
ОО1,
проходящая через эти точки, называется
осью
вращения.
Все точки тела при таком вращении
описывают окружности в плоскостях,
перпендикулярных оси вращения, и с
центрами, лежащими на этой оси (рис.
24); имеют различные линейные скорости
но
при этом поворачиваются на равные углы
.
|
Рис. 24.
Угловая скорость
Быстроту
и направление вращения твёрдого тела
характеризует угловая скорость вращения
(рис.
25).
Рис. 25.
Угловой
скоростью
называют вектор
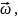который
численно равен первой производной от
угла поворота
по времени и направлен вдоль неподвижной
оси вращения так, чтобы из его конца
вращение тела было видно происходящим
против часовой стрелки (рис.
24):
=
,
(
),
где
– вектор
элементарного поворота.
Вращение
тела называется равномерным,
если численное значение его угловой
скорости не изменяется с течением
времени:
= const.
Для
равномерного вращения справедливо
соотношение:
=
.
Равномерное вращение характеризуется периодом и частотой вращения.
Периодом
вращения Т
называется
промежуток времени,
за
который равномерно вращающееся тело,
совершает один полный оборот (т.е.
поворачивается на угол
= 2
рад.):
Т
=
=
,
(с),
где N – число полных оборотов, совершаемых телом за время t.
Частота вращения n - число оборотов, совершаемых телом за единицу времени:
n
=
=
=
,
(
),
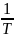т.е.
.
Неравномерное вращение – вращение с переменной угловой скоростью, т.е. = f(t).
Угловое ускорение
Неравномерное
вращение характеризуется угловым
ускорением
,
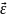которое
показывает быстроту изменения угловой
скорости.
Угловым ускорением называется вектор , равный первой производной по времени от угловой скорости (рис. 26):
=
,
(
)
или
=
.
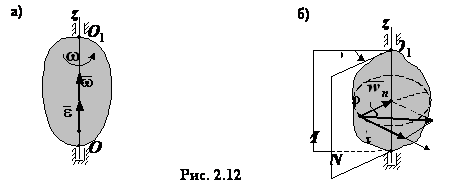
Рис. 26.
Модуль углового ускорения – величина алгебраическая:
ускоренное
вращение;
< 0 – замедленное вращение (рис.
27).
Т.е. вектор углового ускорения направлен вдоль оси вращения (в сторону при укоренном вращении и противоположно – при замедленном вращении).
–
<
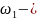
ускоренное вращение; замедленное вращение;
– начальная
угловая скорость.
Рис. 27.
Вращение с постоянным ускорением ( = const) называется равнопеременным вращением (равноускоренным или равнозамедленным).
Для равнопеременного вращения справедливы соотношения:
+
,
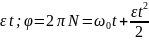где
-–начальная
угловая скорость; N
– число полных оборотов тела.
Аналогия между кинематикой поступательного
и вращательного движений
Поступательное движение |
Вращательное движение |
S -–путь |
– угол поворота |
= |
= |
= |
=
|
S
=
t
+
|
|
Связь между кинематическими величинами, характеризующими поступательное и вращательное движения
Между кинематическими величинами, характеризующими поступательное и вращательное движения тела, существует простая связь:
= R;
=
=
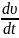(R
)
= R
=
R;
an
=
=
=
R.