З.2. Скорость
Скорость
(часто
обозначается
,
или
от англ. velocity
или фр. vitesse) –
векторная
физическая
величина, характеризующая быстроту
перемещения
и направления движения материальной
точки в пространстве относительно
выбранной системы
отсчёта.
Мгновенная скорость – векторная величина, равная первой производной радиус вектора движущейся точки по времени (скорость тела в данный момент времени или в данной точке траектории):
=
=
,
(
).
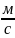Вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки (рис.9).
Рис. 9.
В прямоугольной декартовой системе координат:
=
+
+
.
В
то же время
,
поэтому
=
.
Таким образом, координаты вектора скорости – это скорости изменения соответствующей координаты материальной точки:
,
или
в обозначениях:
=
=
Тогда
модуль скорости можно представить:
=
В
общем случае путь S
отличен от модуля перемещения |Δ
|.
Одинаково, если рассматривать путь dS,
проходимый точкой за малый промежуток
времени dt,
то
dS=|d
|.
Поэтому модуль вектора скорости равен
первой производной от длины пути по
времени:
=
=
.
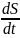Если модуль скорости точки не изменяется с течением времени ( = const), то движение называется равномерным.
Для
равномерного движения справедливо
соотношение:
=
Если модуль скорости изменяется со временем ( = f(t)), то движение называется неравномерным.
Неравномерное
движение характеризуется средней
скоростью (<
>)
и ускорением (
).
Средней
путевой скоростью неравномерного
движения точки на данном участке ее
траектории называется скалярная величина
<
>,
равная отношению длины этого участка,
траектории к продолжительности времени
∆ t
прохождения его точкой
(рис.10): <
>
=
,
где ∆S
– путь, пройдённый точкой за время ∆t.
Рис. 10. Мгновенная и средняя скорости.
В общем случае зависимость скорости неравномерного движения от времени изображена на рис.11, где площадь закрашенной фигуры численно равна пройдённому пути S.
Рис. 11.
В классической механике скорость – величина относительная, т.е. преобразуется при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея.
При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 – х системах отсчёта, который устанавливает классический закон сложения скоростей:
скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно движущейся системы и скорости самой движущейся системы относительно неподвижной:
=
,
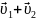где
скорость
точки относительно неподвижной системы
отсчёта,
–
скорость
движущейся системы отсчёта относительно
неподвижной системы,
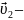скорость
точки относительно движущейся системы
отсчёта.
Пример .
Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.
В
релятивистском случае (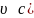
применяется
релятивистский закон сложения скоростей:
=
.
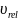Из последней формулы следует, что скорость света – максимальная скорость передачи взаимодействий в природе.
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Ускорение
(обычно
обозначается
)
— производная
скорости
по времени, векторная
величина, показывающая, насколько
изменяется вектор скорости
точки (тела) при её движении за единицу
времени
(т.е. ускорение учитывает не только
изменение величины скорости, но и её
направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,81 м/с каждую секунду, то есть, его ускорение, называемое ускорением свободного падения g = 9,81 м/с².
Производная ускорения по времени, т.е. величина, характеризующая скорость изменения ускорения, называется рывок.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
,
( м/с²).
Модуль ускорения а величина алгебраическая:
а >0 – движение ускоренное (скорость возрастает по величине);
a < 0 – движение замедленное (скорость уменьшается по величине);
а = 0 – движение равномерное.
Если а = const – движение равнопеременное (равноускоренное или равнозамедленное).