3. Энтропия

Понятие «энтропия» введено в науку Р.Клаузиусом в 1862 г. и образовано из двух слов: «эн» - энергия, «тропэ» - превращаю.

Согласно нулевому началу термодинамики изолированная термодинамическая система с течением времени самопроизвольно переходит в состояние термодинамического равновесия и остаётся в нём сколь угодно долго, если внешние условия сохраняются неизменными.

В равновесном состоянии все виды энергии системы переходят в тепловую энергию хаотического движения атомов и молекул, составляющих систему. Никакие макроскопические процессы в такой системе невозможны.

Количественной мерой перехода изолированной системы в равновесное состояние служит энтропия. По мере перехода системы в равновесное состояние её энтропия возрастает и достигает максимума при достижении равновесного состояния.

Энтропия является функцией состояния термодинамической системы, обозначается: [S] = .

Теоретическое обоснование: приведённая теплота, энтропия

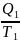
Из выражения для КПД цикла Карно: = = = следует, что = или 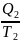= 0, где - количество теплоты, отдаваемое рабочим телом холодильнику, принимаем: < 0.

Тогда последнее соотношение можно записать в виде:

+ = 0 (1)

Отношение теплоты, полученной телом в изотермическом процессе, к температуре теплоотдающего тела называется приведённым количеством теплоты: = . (2)

С учётом формулы (2) формулу (1) представим в виде:

+ = 0, (3)

т.е. для цикла Карно алгебраическая сумма приведённых количеств теплоты равна нулю.

Приведённое количество теплоты, сообщаемое телу на бесконечно малом участке процесса: .

Приведённое количество теплоты для произвольного участка:

= .

Строгий теоретический анализ показывает, что для любого обратимого кругового процесса сумма приведённых количеств теплоты равна нулю:

= 0. (4)

Из равенства нулю интеграла (4) следует, что подинтегральная функция есть полный дифференциал⁴⁰ некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние:

= dS. (5)

Однозначная функция состояния, полным дифференциалом которой является , называется энтропией S, ( ).

Формула (5) справедлива лишь для обратимых процессов, в случае неравновесных необратимых процессов такое представление dS несправедливо.

Свойства энтропии

1). Энтропия определяется с точностью до произвольной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий двух состояний:

∆S = S₂ S₁ = . (6)

Пример: если система (идеальный газ) совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии равно:

∆S₁₂ = S₂ S₁ = = ,

где dU = ; = P dV = RT .

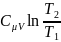Тогда: ∆S₁₂ = = + R = ( + R ln ),

т.е. изменение энтропии ∆S₁₂ идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода.

В общем случае в формуле (6) приращение энтропии ∆S не зависит от пути интегрирования.

2). Абсолютное значение энтропии можно установить с помощью третьего начала термодинамики (теоремы Нернста⁴¹):

Энтропия любого тела стремиться к нулю при стремлении к абсолютному нулю его температуры: = 0.

Таким образом, за начальную точку отсчёта энтропии принимают S₀ = 0 при T = 0 K.

3). Энтропия величина аддитивная, т.е. энтропия системы из нескольких тел является суммой энтропий каждого тела: S = .

4). Как и внутренняя энергия, энтропия есть функция параметров термодинамической системы P, V, T.

5), Процесс, протекающий при постоянной энтропии (S=const) называется изоэнтропийным.

В равновесных процессах без передачи тепла ( 0) энтропия не меняется.

В частности, изоэнтропийным является обратимый адиабатный процесс: для него 0; ∆S = 0, т.е. S = const.

6). При постоянном объёме (V = const) энтропия является монотонно возрастающей функцией внутренней энергии тела.

Действительно, из первого закона термодинамики следует, что при dV = 0 имеем: = dU, тогда dS = 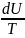. Но температура T > 0 всегда. Поэтому приращения dS и dU имеют один и тот же знак, что и требовалось доказать.

Примеры изменения энтропии в различных процессах

1). При изобарном расширении идеального газа

∆S = C_P ln .

2). При изохорном расширении идеального газа

∆S = C_V ln .

3). При изотермическом расширении идеального газа

∆S = R ln = R ln .

4). При фазовых переходах

Пример: найти изменение энтропии при превращении массы m_л льда при температуре Т₁ в пар (Т_п = 373 К).

Решение

Первый закон термодинамики: dU + = + P dV.

Из уравнения Менделеева – Клапейрона следует: P = 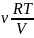=> + dV.

При переходе из одного агрегатного состояния в другое, общее изменение энтропии складывается из изменений в отдельных процессах:

а). Нагревание льда от температуры Т₁ до температуры плавления Т₀ = 273 К:

∆S₁ = 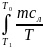dT = mc_л ln ,

где c_л – удельная теплоёмкость льда.

б). Плавление льда: ∆S₂ = = , где - удельная теплота плавления льда.

в). Нагревание воды от температуры Т₀ до температуры кипения Т_к = 273 К:

∆S₃ = dT = mc_в ln , где с_в – удельная теплоёмкость воды.

г). Испарение воды: ∆S₄ = = , где r – удельная теплота парообразования воды.

Тогда общее изменение энтропии:

∆S = ∆S₁ + ∆S₂ + ∆S₃ + ∆S₄ = mc_л ln + + mc_в ln + .

Принцип возрастания энтропии

Энтропия замкнутой системы при любых, происходящих в ней процессах не убывает:

dS 0,

или для конечного процесса: ∆S 0 => S₂ S_1.

Знак равенства относится к обратимому процессу, знак неравенства – к необратимому. Последние две формулы – математическое выражение второго закона термодинамики. Таким образом, введение понятия «энтропия» позволило строго математически сформулировать второе начало термодинамики.

Необратимые процессы приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума. Никакие макроскопические процессы в такой системе невозможны.

Величина изменения энтропии является качественной характеристикой степени необратимости процесса.

Принцип возрастания энтропии относится к изолированным системам. Если система неизолированная, то её энтропия может и убывать.

Вывод: т.к. все реальные процессы необратимые, то все процессы в замкнутой системе ведут к увеличению её энтропии.

Теоретическое обоснование принципа

Рассмотрим замкнутую систему, состоящую из нагревателя, холодильника, рабочего тела и «потребителя» совершаемой работы (тело, обменивающееся с рабочим телом энергией только в форме работы), совершающую цикл Карно. Это обратимый процесс, изменение энтропии которого равно:

∆S = ∆S_р + ∆Sн + ∆S_х + ∆S_п,

где ∆S_р – изменение энтропии рабочего тела; ∆S_н – изменение энтропии нагревателя; ∆S_х – изменение энтропии холодильника; ∆S_п – изменение энтропии «потребителя» работы.

Так как рабочее тело при совершении цикла Карно возвращается в исходное положение, то ∆S_р = 0. Так как «потребитель» работы получает энергию в форме работы, то ∆S_п = 0.

Изменение энтропии нагревателя и холодильника в изотермических процессах:

∆S_н = ; ∆S_х = ,

где и - количество теплоты, полученной рабочим телом за один цикл соответственно от нагревателя ( и холодильника ( .

С учётом выше изложенного изменение энтропии системы равно:

∆S = ( + ).

Так как цикл Карно обратимый, то КПД цикла равен: = =

или = .

В результате получаем, что энтропия замкнутой системы, совершающей обратимый цикл, не изменяется: ∆S_обр. = 0, т.е. S = const.

Все реальные процессы необратимы. Рассмотрим необратимый цикл. КПД необратимого цикла всегда меньше КПД цикла Карно:

< ( и + < 0 | => + < 0,

т.е. энтропия замкнутой системы, совершающей необратимый цикл, возрастает:

∆S_необр. > 0.

Эти выводы можно обобщить для произвольных процессов в замкнутой системе в виде принципа возрастания энтропии.

Основное соотношение термодинамики. Свободная энергия

Первый закон термодинамики: = dU + (1)

Изменение энтропии обратимого процесса: dS = . (2)

Второй закон термодинамики: dS 0. (3)

Из формул (2) и (3) следует: T dS, (4)

где Т – температура тела, сообщающего системе энергию в процессе бесконечно малого изменения состояния системы.

Объединив первый и второй законы термодинамики, получим основное соотношение термодинамики: T dS dU + (5)

Основное соотношение термодинамики для обратимого процесса:

T dS = dU + (6)

или = (dU T dS) = d (U TS) S dT = dF S dT,

где F = U TS – свободная энергия (энергия Гельмгольца⁴²). (7)

Свободная энергия F является разностью двух функций состояний и поэтому то же является функцией состояния термодинамической системы.

Рассмотрим обратимый изотермический процесс, когда dT = 0 и = dF.

При переходе системы из состояния 1 в состояние 2 в обратимом изотермическом процессе: А_изот. = F₁ F₂.

Таким образом, убыль свободной энергии является мерой работы, которую система совершает в обратимом изотермическом процессе.

Из формулы (7) следует: U = F + TS, где TS – связанная энергия. (8)

Внутренняя энергия системы равна сумме свободной и связанной энергий.

Связанная энергия представляет собой ту часть внутренней энергии системы, которая не может быть передана в форме работы в изотермическом процессе. В этом смысле эта часть внутренней энергии является «обесцененной». Связанная энергия тем

больше, чем больше энтропия системы. Поэтому энтропия служит мерой «обесцененности энергии».

Физический смысл энтропии

Энтропия является такой же полноправной физической величиной, характеризующей состояние термодинамической системы, как и объём, давление, температура, внутренняя энергия. Однако в отличие от этих понятий энтропия не используется в повседневной жизни, поэтому с ним не связаны интуитивные представления, всегда облегчающие понимание.

Смысл энтропии:

1). Мера хаоса, неупорядоченности системы.

В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия – наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна энтропия.

2). В статистической физике – мера вероятности осуществления какого-либо макроскопического состояния.

3). Мера необратимого рассеяния энергии, её обесцененности, необратимости процесса.

4). В теории информации – мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы (негаэнтропия (отрицательная энтропия) – количественная мера информации).

5). Чем выше энтропия системы, тем больший временной промежуток прошла она в своём развитии.