Цикл Карно38
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году.
Циклом Карно называется обратимый круговой процесс, состоящий из двух изотерм и двух адиабат.
Среди всех циклов ему принадлежит особое место, т.к. он является наиболее экономичным и лежит в основе действия идеальной тепловой машины. Рассмотрим прямой цикл Карно (рис. 131).
Рис. 131.
Последовательные термодинамические процессы |
|
Изотермическое расширение 1 T= const; V2 > V1 |
A12 = RT1ln = |
Адиабатное расширение 2 3 = 0; T2 < T1 |
A23 = CV (T2 T1) |
Изотермическое
сжатие 3 T=const; V2 < V1 |
A34
=
RT2
ln |
Адиабатное
сжатие 4
= 0; T1 > T2 |
A41 = CV (T1 T2) = A23 |
=
Работа за цикл:
A = A12 + A23 + A34 + A41 = + A23 A23 = (1)
и определяется площадью, ограниченной рассматриваемыми изотермами и адиабатами (рис. 100).
Адиабатические процессы в цикле Карно носят вспомогательный характер: они помогают перейти с одной изотермы на другую. В энергетическом балансе эти процессы не участвуют, т.к. работа адиабатного расширения и адиабатного сжатия компенсируют друг друга.
В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.
Пусть рабочим телом машины, работающей по циклу Карно, является моль ( = 1 моль) идеального газа, тогда теплота , взятая от нагревателя, определяется работой изотермического расширения газа от объёма V1 до объёма V2: = RT1ln . (2)
Теплота, переданная рабочим телом холодильнику, определяется работой изотермического сжатия газа от объёма V3 до объёма V4:
=
RT2
ln
=
RT2
ln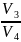
. (3)
Тогда: A = = RT1ln RT2 ln .
Общее выражение КПД для циклического процесса:
= = = 1 (4)
для цикла Карно с идеальным газом примет вид:
=
.
(5)
Из
уравнения Пуассона T
=
const,
применённого к адиабатическим участкам
цикла, легко получить :
=
.
Это
позволяет сократить дробь (5) на величину
Rln
=
R
ln
и
получить
для КПД идеального цикла Карно:
=
< 1
(6)
Так
как абсолютный нуль температур недостижим
(T2
то
КПД идеальной тепловой машины всегда
меньше единицы.
Формула (6) выражает теорему Карно:
КПД
идеальной тепловой машины,
работающей по циклу Карно,
максимален и не зависит от природы
рабочего вещества и конструкции тепловой
машины, он
определяется только по температурам
нагревателя (
)
и холодильника (T2).
Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно.
КПД необратимой тепловой машины всегда меньше, чем обратимой, работающей в аналогичных условиях (т.е. с теми же нагревателем и холодильником). Так КПД современных паровых машин не превышает 25%, двигателей внутреннего сгорания – 40%. Между тем теоретический предел лежит выше. Снижение КПД реальных тепловых машин по сравнению с теоретическим вызвано необратимыми процессами, которые происходят в самой тепловой машине (теплопроводностью и т.п.).
Пути повышения КПД тепловых машин: устранение (по мере возможности) и ослабление необратимых процессов. Если необратимый процесс всё же произошёл, то нет ни какой возможности устранить его последствия, ведущие к ухудшению работы двигателя.
В тепловых двигателях стремятся обеспечить наилучшую отдачу тепла рабочему телу и наименьшую потерю тепла рабочим веществом. Так, чтобы сократить число необратимых процессов теплообмена в двигателях внутреннего сгорания, «внесли» топку внутрь рабочего цилиндра. Осуществляют и другие мероприятия.