1.12. Уравнение Менделеева27 - Клапейрона28

Уравнение Менделеева – Клапейрона -–уравнение состояния идеального газа, устанавливающее связь между его объемом V, давлением P и абсолютной температурой T.

Рассматриваем идеальный газ. Уравнение состояния идеального газа:

P = n₀ k T | V,

где V – объём газа.

Получаем: PV = n₀V kT. Учтём, что N = n₀V = N_a – число частиц газа, где -–число молей газа, N_a – постоянная Авогадро.

Тогда получаем: PV = NkT = N_a kT, где N_a k = R = 8,31 – универсальная газовая постоянная.

Окончательно получаем: PV= RT.

Последнее уравнение является уравнением состояния идеального газа и называется уравнением Менделеева – Клапейрона.

Частные случаи уравнения Менделеева – Клапейрона

Рассматриваем идеальный газ постоянной массы (m = const):

Изотермический процесс – процесс, протекающий в системе постоянной массы при постоянной температуре (T=const).

Процесс описывается законом Бойля²⁹- Мариотта³⁰: произведение объёма данной массы газа на его давление постоянно при постоянной температуре: PV=const.

Изобарный процесс – процесс, протекающий в системе постоянной массы при постоянном давлении (P=const).

Процесс описывается законом Гей – Люссака³¹: отношение объёма данной массы газа его абсолютной температуре при постоянном давлении есть величина постоянная:

Изохорный процесс – процесс, протекающий в системе постоянной массы при постоянном объёме (V = const).

Процесс описывается законом Шарля³² : отношение давление данной массы газа при постоянном объемё его абсолютной температуре есть величина постоянная:

Закон Дальтона³³

В состоянии теплового равновесия давление в смеси идеальных газов равно сумме давлений каждой компоненты смеси:

P = P₁ + P₂ + … +P_n =

1.13. Барометрическая формула. Распределение Больцмана

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Рассмотрим идеальный газ в равновесном состоянии внутри куба с ребром l. Давление газа на рани куба обусловлено ударами молекул. Молекулы находятся в однородном поле тяготения, температура постоянна, масса всех молекул одинакова.

Действительно, молекулы любого газа в реальности находятся в поле тяготения Земли.

Тяготение и тепловое движение приводят газ в состояние, при котором его концентрация и давление убывают с высотой.

Если считать, что плотность газа по всему объёму постоянна ( то аэростатическое давление на глубине h , будет равно:

P =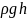 , (1)

где g – ускорение свободного падения.

Формулой (1) можно пользоваться для вычисления давления очень тонких горизонтальных слоёв газа.

Пусть P – давление газа на высоте h. Тогда с увеличением высоты на бесконечно малую величину dh давление понизится на величину:

dP = (2)

Из уравнения Менделеева – Клапейрона следует, что плотность газа равна: . (3)

Тогда: dP = (4)

или = . (5)

Проинтегрируем (5) от 0 до h (при T = const):

= , где P₀ – давление на высоте h = 0.

Тогда барометрическая формула примет вид:

P = P₀ ,

(6)

h = 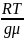ln .

Давление газа связано с концентрацией молекул:

P= n₀ k T, (7)

где n₀ – число молекул в единице объёма (концентрация молекул).

При T = const, получим:

= , (8)

где n₀₀ – концентрация молекул при давлении Р₀ (при h = 0).

Тогда уравнение (6) примет вид:

Так как = 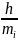, где П = m_i g h – потенциальная энергия молекулы в поле тяготения Земли.

Получаем распределение Больцмана:

Т.е. при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

При Т , то n₀ n₀₀ , т.е. повышение температуры ведёт к выравниванию концентрации молекул газа по объёму.

Если Т 0 К, то n₀ 0, т.е. все молекулы под действием силы тяжести будут опускаться на дно сосуда.

Атмосфера Земли существует лишь вследствие теплового движения частиц воздуха.

Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Чем выше температура , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести mg (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести mg может изменяться за счёт двух величин: ускорения g и массы частиц m. Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте (рис. 115). На рис. 115 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

Рис. 115.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.