
- •Оглавление
- •Часть I. Механика 4
- •Часть II. Молекулярная физика и термодинамика 81
- •Часть I. Механика
- •Кинематика
- •Основные понятия кинематики
- •З.2. Скорость
- •Среднее ускорение
- •Мгновенное ускорение
- •Ускорение точки при прямолинейном движении
- •Кинематика вращательного движения
- •4. Динамика
- •Закон всемирного тяготения
- •2). Сила тяжести
- •3). Сила реакции опоры
- •4). Сила трения
- •Виды трения
- •5). Сила упругости
- •4.4. Импульс. Закон сохранения импульса
- •История появления термина
- •4.5. Законы Ньютона
- •Замечания:
- •4.6. Энергия
- •Потенциальная энергия тела, поднятого над поверхностью Земли
- •Закон сохранения энергии в механике
- •4.7. Динамика вращательного движения
- •2). Пара сил
- •Момент импульса
- •Механический (классический) принцип относительности (принцип относительности Галилея)
- •Основы механики жидкостей и газов
- •Архимед из СиракузArchimedes of Siracuse, ок. 287–212 г. До н. Э.
- •Условие плавания тел
- •Вязкость газов
- •Часть II. Молекулярная физика и термодинамика
- •I. Молекулярная физика
- •1.1. Предмет молекулярной физики
- •1.2. Внесистемные единицы измерения величин в микрофизике физике
- •1.3. Основные положения молекулярно-кинетической теории строения вещества
- •1.4. Число степеней свободы молекул
- •1.5. Термодинамическая система. Термодинамические состояние и процесс
- •1.6. Статистический метод в молекулярной физике
- •1.7. Количество вещества. Масса молекул
- •1.8. Идеальный газ
- •1.9. Закон равномерного распределения энергии по степеням свободы молекул
- •1.10. Закон Максвелла25 о распределении молекул идеального газа по скоростям
- •Вывод распределения по Максвеллу
- •Границы применимости
- •Зависимость функции распределения Максвелла от температуры.
- •Характерные скорости Наиболее вероятная скорость
- •Средняя скорость
- •1.11. Основное уравнение молекулярно – кинетической теории (уравнение Клаузиуса26)
- •1.12. Уравнение Менделеева27 - Клапейрона28
- •1.13. Барометрическая формула. Распределение Больцмана
- •1.14. Средняя длина свободного пробега молекул
- •II. Термодинамика
- •2 .1. Термодинамический метод
- •2.2. Внутренняя энергия
- •Два способа изменения внутренней энергии. Теплота и работа
- •Первое начало термодинамики
- •Нулевое начало термодинамики
- •Теплоёмкость
- •1). Молярная теплоёмкость идеального газа при постоянном объёме
- •2). Молярная теплоёмкость идеального газа при постоянном давлении Уравнение Майера
- •Термический кпд для кругового процесса
- •Из истории тепловых двигателей
- •Цикл Карно38
- •Второе начало термодинамики
- •Энтропия
- •2.16. Статистическая интерпретация второго начала термодинамики
- •Реальные газы
- •Жидкости
- •Твёрдые тела
- •Изоморфизм и полиморфизм кристаллов
- •Кристаллические вещества Типы кристаллических решеток
- •Общая характеристика
- •Классификация решёток по симметрии
- •Объём ячейки
Вывод распределения по Максвеллу
Получим теперь формулу распределения так, как это делал сам Джеймс Клерк Максвелл.
Рассмотрим
пространство скоростных точек [каждую
скорость молекулы представляем как
точку (скоростную точку) в системе
координат (
 в стационарном
состоянии газа. Выберем
бесконечно
малый элемент объема (d
в стационарном
состоянии газа. Выберем
бесконечно
малый элемент объема (d d
d d
d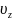 ).
Так как газ стационарный, количество
скоростных точек в (d
d
d
)
остается неизменным с течением времени.
Пространство скоростей изотропно,
поэтому функции плотности
вероятности для всех
направлений одинаковы.
).
Так как газ стационарный, количество
скоростных точек в (d
d
d
)
остается неизменным с течением времени.
Пространство скоростей изотропно,
поэтому функции плотности
вероятности для всех
направлений одинаковы.
dP(
)
=
(
)
d
,
dP( )
=
(
)
d
,
dP(
)
=
(
)
d
.
)
=
(
)
d
,
dP(
)
=
(
)
d
.
Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента скорости молекулы не зависит от y и z - компонент.
dP( )
=
(
)
(
)
(
)
d
d
)
=
(
)
(
)
(
)
d
d – фактическая вероятность
нахождения скоростной точки в объёме
(d
d
),
где f(
)
=
(
)
(
)
(
).
– фактическая вероятность
нахождения скоростной точки в объёме
(d
d
),
где f(
)
=
(
)
(
)
(
).
ln
f(
)
= ln
(
)
+ ln
(
)
+ ln
(
)
|
 .
.
 =
=
 ,
,
 =
=
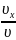 ,
,

 =
=
 .
.
Правая часть не зависит от и , значит и левая от и не зависит. Однако и равноправны, следовательно, левая часть не зависит также и от . Значит, данное выражение может лишь равняться некоторой константе.
=

=

 =
A
=
A
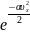 .
.
 d
= 1
A
d
= 1
A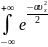 d
= A
d
= A
 = 1
=
= 1
=
 .
.
Теперь нужно сделать принципиальный шаг — ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):
<
 > =
> =
 kT,
kT,
где
k=1,38•
10-23
– постоянная
Больцмана;
=
 Ввиду
равноправия всех направлений: <
Ввиду
равноправия всех направлений: < = <
= < = <
= < =
=
 <
<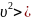 =
=
 .
.
Чтобы
найти среднее значение
 ,
проинтегрируем её вместе с функцией
плотности вероятности от минус до плюс
бесконечности:
,
проинтегрируем её вместе с функцией
плотности вероятности от минус до плюс
бесконечности:
=
 d
=
d
=
 d
=
d
=
 .
.
Отсюда
найдём
:
=
 .
.
Функция
распределения плотности вероятности
для
 аналогично
для
аналогично
для
 ):
=
):
=

 .
.
Теперь
рассмотрим распределение по величине
скорости. Вернемся в пространство
скоростных точек. Все точки с модулем
скорости
 лежат в шаровом слое радиуса
и толщины d
,
и (d
d
d
)
– объем этого шарового слоя.
лежат в шаровом слое радиуса
и толщины d
,
и (d
d
d
)
– объем этого шарового слоя.
dP ( ) = ( ) ( ) ( ) d d .
dP
(
)
=
 d
d
d
d
d
d
Учтём,
что: dP
(
)
= dP(
);
d
d
d
= 4 d
,
получим:
d
,
получим:
dP(
)
= 4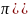 d
,
d
,
где F( ) = 4 . Тогда окончательно получим: dP( ) = F( ) d .
Таким
образом, мы получили функцию плотности
вероятности F ( ,
которая и является распределением
Максвелла.
,
которая и является распределением
Максвелла.
Границы применимости
Условия применимости распределения Максвелла:
1. Равновесное состояние системы, состоящей из большого числа частиц.
2. Изотропная система.
3. Классическая система. Это значит, что система должна быть не релятивистской и не квантовой (взаимодействие частиц допускается, но только зависящее от относительного положения частиц).
Относительное
число молекул
 ,
со скоростями, лежащими в интервале от
до
+d
,
со скоростями, лежащими в интервале от
до
+d рассчитывается как площадь заштрихованной
полоски на рис. 111. Площадь, которая
ограничена кривой распределения и осью
абсцисс, равна единице. Это значит, что
функция f(
рассчитывается как площадь заштрихованной
полоски на рис. 111. Площадь, которая
ограничена кривой распределения и осью
абсцисс, равна единице. Это значит, что
функция f( )
удовлетворяет условию нормировки :
)
удовлетворяет условию нормировки :
 d
=
1.
d
=
1.
Вид функции распределения f ) (рис. 82):

Рис. 111.
На
рис. 111:
 -–наиболее вероятная скорость молекул,
соответствует максимуму кривой; <
- средняя скорость молекул газа; <
-–наиболее вероятная скорость молекул,
соответствует максимуму кривой; <
- средняя скорость молекул газа; < >
- cредняя
квадратичная скорость молекул газа.
>
- cредняя
квадратичная скорость молекул газа.
С ростом температуры максимум кривой распределения смещается в сторону бо′льших температур (рис. 112).

Рис. 112.
