1.8. Идеальный газ

Идеальный газ — математическая модель газа, в которой предполагается, что: 1) потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём молекул газа пренебрежимо мал; 3) между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

В расширенной модели идеального газа частицы, из которого он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).

Идеальный газ реально не существует.

1.9. Закон равномерного распределения энергии по степеням свободы молекул

Закон доказан Л.Больцманом²⁴ методом классической статистической физики, исходя из предположения, что движение молекул подчиняется законам классической механики:

Для статистической системы, которая находится в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kT,

где k = 1,38 10^-23 - постоянная Больцмана.

Если молекула имеет i степеней свободы, то её средняя кинетическая энергия равна: < > = kT.

Закон Больцмана лежит в основе всей теоpии идеальных газов. Однако, закон оказался неточным, т.к. молекулы – квантовые частицы.

1.10. Закон Максвелла25 о распределении молекул идеального газа по скоростям

Понятие о функции распределения

Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее, чем х, где х — произвольное действительное число.

Функция распределения, основное понятие статистической физики; характеризует плотность вероятности распределения частиц статистической системы по фазовому пространству (т.е. по координатам (q_i и импульсам p_i) в классической статистической физике или вероятность распределения по квантовомеханическим состояниям в квантовой статистике.

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.

Функция распределения молекул идеального газа по скоростям

Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного  (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т  скорости, заключенные в интервале от     до + d .  

Идеальный газ – система из большого числа свободных невзаимодействующих частиц, находящихся в непрерывном хаотическом движении, часто сталкивающихся друг с другом. Поэтому в газе при постоянных внешних параметрах устанавливается равновесное состояние, которому соответствует определённое распределение частиц в пространстве по направлениям движения и скоростям. При равновесии средние скорости и число частиц, движущихся в разных направлениях, оказывается одинаковым, о чём свидетельствует отсутствие направленного потока газа при равновесии.

Абсолютная величина скорости молекул, а также проекции скорости на любую ось могут принимать непрерывные значения от нуля до бесконечности. Значит, должна существовать непрерывная функция распределения скоростей f( ), показывающая относительное количество молекул, движущихся в единичном интервале скоростей со скоростью, близкой к скорости .

На языке теории вероятности d есть плотность вероятности того, что молекула имеет скорость, лежащую в интервале от до + d . Тогда сама вероятность описывается выражением: dW = f( ) •d .

Нахождение функции распределения f( ) молекул по скоростям является главной задачей молекулярно-кинетической теории. Это объясняется тем, что согласно теории вероятности любой функции F( ) (это может быть внутренняя энергия, длина свободного пробега или любая другая функция состояния газа) определяется следующим интегралом:

< F( )> = f( ) •d .

Впервые найти функцию распределения по скоростям удалось Д.Максвеллу, который исходил из следующих предположений:

1. Идеальный газ состоит из большого числа N одинаковых молекул;

2. Температура газа постоянна (T= const);

3. Молекулы газа совершают тепловое хаотическое движение;

4. На газ не действуют силовые поля.

Функция распределения молекул по скоростям f )= 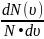определяет относительное число молекул , скорости которых лежат в интервале от до + d .

Используя методы теории вероятностей, Максвелл нашел функцию f ( ) -–закон распределения молекул идеального газа по скоростям:

f( ) = 4 ( )^{3/2 2} еxp { },

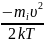где f( ) зависит от рода газа (m_i – масса молекулы) и от параметров состояния (температуры Т).