1.6. Статистический метод в молекулярной физике

Молекулярно-кинетическая теория (МКТ) ставит целью исследовать макроскопические свойства тел, которые непосредственно наблюдаются на опыте (давление, температура и т.п.), как суммарный результат действия молекул.

В МКТ термодинамические системы – системы, состоящие из большого числа частиц. Поэтому МКТ пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь средними величинами, которые характеризуют движение их огромной совокупности:

1). Средняя скорость: < = = ,

где -–скорость i-той молекулы, N – число молекул.

2). Средняя квадратичная скорость:

< = = .

3). Средняя энергия < >.

Поэтому МКТ называют также статистической физикой.

В классической статистической физике молекулы рассматриваются как классические частицы, движение которых подчиняется законам классической механике, в т.ч. второму закону Ньютона.

1.7. Количество вещества. Масса молекул

Количество вещества (n,  — физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе.

Под структурными единицами понимаются любые частицы, из которых состоит вещество (атомы, молекулы, ионы, электроны или любые другие частицы). Единица измерения количества вещества в Международной системе единиц (СИ) — моль.

Эта физическая величина используется для измерения макроскопических количеств веществ в тех случаях, когда для численного описания изучаемых процессов необходимо принимать во внимание микроскопическое строение вещества, например, в химии, при изучении процессов электролиза, или в термодинамике, при описании уравнений состояния идеального газа.

При описании химических реакций, количество вещества является более удобной величиной, чем масса, так как молекулы взаимодействуют независимо от их массы в количествах, кратных целым числам.

Например, для реакции горения водорода (2H₂ + O₂ → 2H₂O) требуется в два раза большее количество вещества водорода, чем кислорода. При этом масса водорода, участвующего в реакции, примерно в 8 раз меньше массы кислорода (так как атомная масса водорода примерно в 16 раз меньше атомной массы кислорода). Таким образом, использование количества вещества облегчает интерпретацию уравнений реакций: соотношение между количествами реагирующих веществ непосредственно отражается коэффициентами в уравнениях.

Так как использовать в расчётах непосредственно количество молекул неудобно, потому что это число в реальных опытах слишком велико, вместо измерения количества молекул «в штуках», их измеряют в молях.

Моль – количество вещества, содержащее столько же молекул (атомов, ионов), сколько атомов содержится в 0,012 кг изотопа углерода .

Число частиц, содержащихся в моле вещества называется постоянной Авогадро²³: N_a = 6,02 .

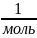В моле любого вещества (твёрдого, жидкого, газообразного) содержится одинаковое количество молекул, равное N_a.

Моль -– это количество вещества, содержащее 6,02·10²³ атомов или молекул этого вещества.

Так как массы различных молекул отличны друг от друга, то одинаковые количества различных веществ имеют разную массу.

Массу моля называют молярной массой: , , где m – масса вещества.

Относительная молекулярная масса M_r – величина безразмерная: M_r = 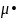10³.

Если m_i – масса одной i – той молекулы, то = m_i• N_a.

Число молекул, содержащихся в произвольной массе вещества:

N = • N_a.

По закону Авогадро, количество газообразного вещества так же можно определить на основании его объёма: = V / V_m, где V — объём газа (при нормальных условиях), V_m — молярный объём газа при н. у., равный 22,4 л/моль.

Таким образом, справедлива формула, объединяющая основные расчёты с количеством вещества:

= = =

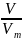
Молярная масса численно всегда совпадает с молекулярной массой (или атомной массой -–если вещество состоит не из молекул, а из атомов). В таблице 1 для иллюстрации приведены молярные массы М для нескольких веществ разного строения.

Таблица 1. Молярные массы различных веществ

Вещество	Молекулярная или атомная масса (округлена)	молярная масса •10-3
Вода Н2О	18 а.е.м.	18 кг/моль
СаО	56 а.е.м.	56 кг/моль
Углерод 12С	12 а.е.м.	12 кг/моль
Медь Cu	63,5 a.e.м.	63,5 кг/моль
Молекула хлора Cl2	71 а.е.м.	71 кг/моль

Количественно масса 1 моль вещества – масса вещества в граммах, численно равная его атомной или молекулярной массе.

Пример: молекулярная масса воды H₂O равна 18 а.е.м. (атомная масса водорода -–1, кислорода – 16, итого 1+1+16=18). Значит, один моль воды равен по массе 18 граммов, и эта масса воды содержит 6,02·10²³ молекул воды.

Итак, один моль любого вещества содержит 6,02 · 10²³ молекул, атомов или других частиц.

Например, 1 моль воды H₂O содержит 6 · 10²³ молекул H₂O;

1 моль железа Fe содержит 6 · 10²³ атомов Fe.

1 моль хлора Cl₂ содержит 6 · 10²³ молекул Cl₂.

В то же время 1 моль хлора Cl₂ содержит 2 моль атомов хлора Cl.