Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где <u> — средняя скорость теплового движения молекул, < − средняя длина свободного пробега. Из этого выражения, в частности, следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность прямо пропорциональна давлению, а <  — обратно пропорциональна.

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа , растущей с температурой как .

Прибор для измерения вязкости называется вискозиметром.

Качественно существенное отличие сил вязкого трения от сухого трения в том, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, т.е. для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.

Ламинарный и турбулентный режимы течения жидкостей

Существует два режима течения жидкостей: ламинарный и турбулентный.

Ламинарное течение (лат. lāmina — «пластинка») – упорядоченное течение жидкости и газа, при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения (рис. 100).

Рис. 100.

Установившееся течение идеальной жидкости всегда ламинарное при любых скоростях течения, т.к. в такой жидкости отсутствуют силы внутреннего трения. В случае реальных жидкостей ламинарное течение наблюдается у очень вязких жидкостей или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. В частности, ламинарное течение имеет место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, образующемся при обтекании их жидкостью или газом и др.

При ламинарном течении скорость слоёв изменяется от оси трубки к стенкам по параболическому закону (рис. 101).

Рис. 101.

С увеличением скорости движения жидкости ламинарное течение в некоторый момент времени переходит в турбулентное течение. При этом существенно изменяются все его свойства, например, структура потока, профиль скоростей, закон сопротивления.

Турбулентное течение (от лат. turbulentus - бурный, беспорядочный) – форма течения жидкости или газа, при которой их элементы совершают неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями жидкости или газа (рис. 102).

Рис. 102.

Большинство течений жидкостей и газов турбулентное как в природе (движение воздуха в земной атмосфере, воды в реках и морях, газа в атмосферах Солнца и звёзд и в межзвёздных туманностях и т.п.), так и в технических устройствах (трубах, каналах, струях, в пограничных слоях около твёрдых тел, в следах за такими телами и т.п.).

Турбулентное течение нестационарно: скорость и давление в каждой точке потока колеблется около некоторых средних значений. Это связано с тем, что при турбулентном течении частицы жидкости приобретают составляющие скоростей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой, а их скорости в различных слоях мало отличаются.

В результате перемешивания слоёв жидкости средняя скорость течения практически одинакова по всему сечению трубки тока (трубы). Только в очень тонком слое, примыкающем к стенкам трубы, скорость быстро падает до нуля. Изменение средней скорости турбулентного течения в зависимости от расстояния от оси трубы представлено на рис. 103.

Рис. 103.

При турбулентном течении резко возрастают силы внутреннего трения, т.к. между стенкой и турбулентным потоком вследствие явления прилипания возникает очень тонкий слой с большим поперечным градиентом скорости. Увеличение внутреннего трения обусловлено ещё и тем, что коэффициент вязкости возрастает при переходе к турбулентному движению.

Английский учёный О. Рейнольдс²⁰доказал, что характер течения жидкости зависит от безразмерной величины, называемой числом Рейнольдса: R_e = ,

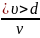где - кинематическая вязкость, < > - средняя по сечению трубы скорость течения жидкости, d – характерный линейный размер, например, диаметр трубы.

Опыт показывает, что при малых значениях числа Рейнольдса R_e течение жидкости (газа) является ламинарным, а при больших – турбулентным.

Значение числа Рейнольдса, характеризующее переход от ламинарного к турбулентному течению, называют критическим - R_{e кр.}.

Изучая на опыте течение жидкости (газа) по круглым трубам в обычных условиях, установили, что R_{e кр.} 2300.

Если для некоторого потока R_e < R_{e кр.}, то течение будет ламинарным, если R_e >R_{e кр.} – течение турбулентное. При R_e, близком R_{e кр.} , ламинарное течение неустойчиво и очень чувствительно к разного рода факторам (резкие переходы в трубе, шероховатость стенок, вибрации и др.). Устраняя эти факторы, можно добиться того, что ламинарное течение сохраняется вплоть до значения R_e = 10000. Это явление называется затягиванием ламинарного режима. «Затягивание» приобретает большое практическое значение в связи с созданием длинных линий газо- и нефтепроводов, т.к. силы внутреннего трения при ламинарном течении значительно меньше, чем при турбулентном: при одном и том же расходе перекачка жидкости при ламинарном течении требует меньших перепадов давления, т.е. меньших затрат энергии.

Уравнение неразрывности струи

Рассмотрим трубку тока переменного сечения S₁ и S₂, по которой течёт идеальная несжимаемая жидкость (рис. 104).

Рис.104.

За время dt через сечение S₁ проходит объём жидкости V₁ = S₁ dt, через сечение S₂ - объём жидкости V₂ = S₂ dt. Следовательно, за 1с через сечение S₁ пройдёт объём жидкости V₁^′ = S₁ где - скорость течения жидкости в сечении S₁, а через сечение S₂ за 1с - V₂^′ = S₂ , где - скорость течения жидкости в сечении S₂.

Так как жидкость несжимаемая, то через сечение S₁ пройдёт такой же объём жидкости, как и через сечение S₂ , т.е. S₁ = S₂ .

Произведение скорости стационарного течения идеальной несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока:

S = const.

Последнее соотношение, выражающее закон сохранения массы для любого объёма жидкости (газа), называется уравнением неразрывности струи.

Следствие из уравнения неразрывности струи: если жидкость движется по трубе переменного сечения, то скорость ее движения обратно пропорциональна площади сечения трубок: = .

На частицы реальной жидкости действуют силы трения со стороны стенок трубы и со стороны соседних частиц. Поэтому скорость частиц жидкости в поперечном сечении трубы различна: она максимальна в центре трубы и уменьшается до нуля у ее стенок. В этом случае в формуле уравнения неразрывности - это средняя скорость течения жидкости в данном сечении.

Уравнение Бернулли²¹

Следствием закона сохранения механической энергии для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли, сформулированное в 1738 г.

Рассматривается стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 105). Различные части трубы находяться на разных высотах.

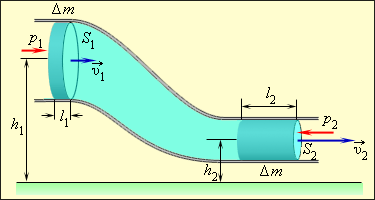
Рис. 105.

Исходя из закона сохранения механической энергии и уравнения неразрывности струи Д.Бернулли получил следующее уравнение:

+ + P = const,

где - плотность жидкости, – динамическое давление, - гидростатическое давление, P – статическое давление (давление жидкости на поверхность обтекаемого тела).

При стационарном течении идеальной жидкости полное давление, равное сумме статического, динамического и гидростатического давлений, одинаково во всех поперечных сечениях трубки тока.

Для горизонтальной трубки тока (h₁ = h₂) уравнение Бернулли примет вид:

+ P = const,

где P₀ = + P – полное давление.

Из уравнения Бернулли и уравнения неразрывности следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость течения жидкости больше в местах сужения, а статическое давление – в более широких местах, т.е. там, где скорость меньше.

Уравнение Бернулли хорошо выполняется для реальных жидкостей, внутреннее трение которых невелико. Поэтому уравнение Бернулли широко применяется в гидравлике при расчёте течения жидкостей и газов в трубопроводах, при расчёте компрессоров, турбин, насосов и других гидравлических и газовых машин.

Теоретическое обоснование уравнения Бернулли

За промежуток времени Δt жидкость в трубе сечением S₁ переместится на l₁ = υ₁Δt, а в трубе сечением S₂ – на l₂ = υ₂Δt, где υ₁ и υ₂ – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде: ∆V = l₁S₁ = l₂S₂ или S₁ = S₂. Здесь ΔV – объем жидкости, протекшей через сечения S₁ и S₂.

Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.

Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.

При перемещении жидкости силы давления совершают работу:

ΔA = p1S1l1 – p2S2l2 = p1S1υ1Δt – p2S2υ2Δt = (p1 – p2)ΔV.

Работа ΔA сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком.

Изменения, произошедшие за время Δt в выделенной части жидкости, заключенной между сечениями S₁ и S₂ в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δm = ρΔV (ρ – плотность жидкости) из одной части трубы сечением S₁ в другую часть сечением S₂ (заштрихованные объемы на рис. 99). Закон сохранения механической энергии для этой массы имеет вид:

E2 – E1 = ΔA = (p1 – p2)ΔV,

где E₁ и E₂ – полные механические энергии массы Δm в поле тяготения:

E₁ = + ∆mgh₁; E₂ = + ∆mgh₂.

Отсюда следует: + gh₁ + P₁ = + gh₂ + P₂.

Это и есть уравнение Бернулли. Из него следует, что сумма

+ gh + P = const.

остается неизменной вдоль всей трубы.

Уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.

Примеры.

1). Рассмотрим истечение жидкости из широкого сосуда (рис. 106).

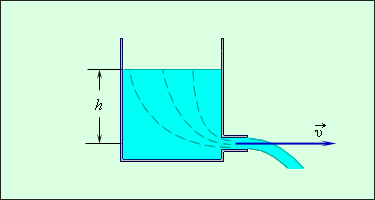
Рис. 106.

Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:

+ P₀ = + P₀,

где P₀ – атмосферное давление, – перепад высоты вдоль линии тока. Таким образом,

= .

Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.

2). Подъёмная сила крыла самолёта

Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла. На рис. 107 изображены линии тока воздуха при обтекании крыла самолета. Из-за специального профиля крыла и наличия угла атаки, т. е. угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом. Поэтому на рис. 107 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила действующая на крыло. Вертикальная составляющая _y этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая _x представляет собой силу сопротивления среды.

Рисунок 107.

Линии тока при обтекании крыла самолета и возникновение подъемной силы. α – угол атаки.

Теория подъемной силы крыла самолета была создана Н. Е. Жуковским. Он показал, что при обтекании крыла существенную роль играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла (зеленые стрелки на рис. 107). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы.

Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса.

Рис. 108 иллюстрирует обтекание вращающегося цилиндра набегающим потоком. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.

Рис. 108.

Обтекание вращающегося цилиндра набегающим потоком воздуха.