4.7. Динамика вращательного движения

Из всех видов вращательного движения будем рассматривать только вращение тела вокруг неподвижной оси.

Момент силы

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки – полюса) и относительно оси.

Моментом силы (синонимы: крутящий момент, вращатльный момент, вертящий момент, вращающий момент) относительно неподвижной точки 0 (полюса) называется векторная величина 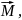равная векторному произведению радиус-вектора проведённого из точки 0 (полюса) в точку А приложения силы, на вектор силы = [ (Н•м). ( Рис. 66).

Рис. 66.

Направлен вектор перпендикулярно плоскости, проходящей через 0 и Сторона, куда направляется выбирается условно. При правой системе координат вектор направляют в ту сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки.

Момент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика (рис.67).

Рис. 67.

Модуль момента силы: M ₌ F•r•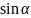 = F•l, где: M – момент силы, F – приложенная сила, r – расстояние от центра вращения до места приложения силы, .l = r ^.sin α  – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы, α — угол, между вектором силы и вектором положения . Т.е. численно момент силы равен произведению модуля силы F на плечо l.

Направление момента силы можно также определить по правилу левой руки: четыре пальца левой руки поставить по направлению первого сомножителя , второй сомножитель  входит в ладонь, отогнутый под прямым углом большой палец укажет направления момента силы  . Вектор момента силы всегда перпендикулярен плоскости, в которой лежат векторы  и .

Моментом силы  относительно неподвижной оси Z называется скалярная величина равная проекции на эту ось вектора момента силы , определённого относительно произвольной точки O данной оси Z (рис. 68). Момент силы относительно оси величина алгебраическая.

Рис. 68.

Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов: если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:

= М₁ + М₂ + … + М_n = 0.

Считают момент силы положительным (M_i >0), если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным (M_i >0) в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.69, силам F₁ и F₂ следует приписать положительный момент, а силе F₃— отрицательный.

Рис. 69.

Примеры:

1). Гаечный ключ

Рис. 70. Момент силы, приложенный к гаечному ключу, направлен от зрителя.

2). Пусть на тело, в плоскости перпендикулярной оси вращения 0₁0₂ действует сила . Разложим эту силу на две составляющие: _n и (рис. 70).

Сила _n пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей тело будет совершать вращательное движение вокруг оси 0₁0₂. Расстояние r от оси вращения до линии вдоль которой действует сила , называется плечом силы . Моментом силы относительно точки 0 называется произведение модуля силы F на плечо r : M = F • r.

С учетом, что F = F• , то момент силы M = F•r• С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора проведенного в точку приложения силы на эту силу.

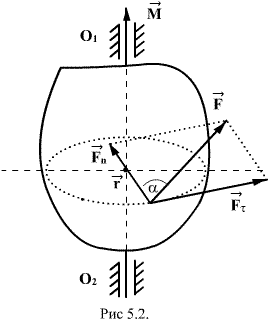
Рис. 70.

Таким образом, момент силы относительно точки 0 является векторной величиной и равен: =[ , ],

Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы и , и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от к происходит против часовой стрелки).

Примеры:

1). Рычаги

Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его вокруг этой оси.

Примерами рычагов являются гаечные ключи, различные педали, щипцы для раскалывания орехов, двери и т. д.

Согласно правилу моментов, рычаг (любого рода) уравновешен только тогда, когда М₁ = М₂. Поскольку

М₁=F₁l₁ и М₂=F₂l₂,

Получаем F₁l₁ = F₂l₂. Из последней формулы следует, что

F₁/F₂ = l₂/l₁,    

т. е. при равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их плечам. Т..е. с помощью рычага можно получить выигрыш в силе тем больший, чем больше соотношение плеч. Это широко используют на практике.