
- •Оглавление
- •Часть I. Механика 4
- •Часть II. Молекулярная физика и термодинамика 81
- •Часть I. Механика
- •Кинематика
- •Основные понятия кинематики
- •З.2. Скорость
- •Среднее ускорение
- •Мгновенное ускорение
- •Ускорение точки при прямолинейном движении
- •Кинематика вращательного движения
- •4. Динамика
- •Закон всемирного тяготения
- •2). Сила тяжести
- •3). Сила реакции опоры
- •4). Сила трения
- •Виды трения
- •5). Сила упругости
- •4.4. Импульс. Закон сохранения импульса
- •История появления термина
- •4.5. Законы Ньютона
- •Замечания:
- •4.6. Энергия
- •Потенциальная энергия тела, поднятого над поверхностью Земли
- •Закон сохранения энергии в механике
- •4.7. Динамика вращательного движения
- •2). Пара сил
- •Момент импульса
- •Механический (классический) принцип относительности (принцип относительности Галилея)
- •Основы механики жидкостей и газов
- •Архимед из СиракузArchimedes of Siracuse, ок. 287–212 г. До н. Э.
- •Условие плавания тел
- •Вязкость газов
- •Часть II. Молекулярная физика и термодинамика
- •I. Молекулярная физика
- •1.1. Предмет молекулярной физики
- •1.2. Внесистемные единицы измерения величин в микрофизике физике
- •1.3. Основные положения молекулярно-кинетической теории строения вещества
- •1.4. Число степеней свободы молекул
- •1.5. Термодинамическая система. Термодинамические состояние и процесс
- •1.6. Статистический метод в молекулярной физике
- •1.7. Количество вещества. Масса молекул
- •1.8. Идеальный газ
- •1.9. Закон равномерного распределения энергии по степеням свободы молекул
- •1.10. Закон Максвелла25 о распределении молекул идеального газа по скоростям
- •Вывод распределения по Максвеллу
- •Границы применимости
- •Зависимость функции распределения Максвелла от температуры.
- •Характерные скорости Наиболее вероятная скорость
- •Средняя скорость
- •1.11. Основное уравнение молекулярно – кинетической теории (уравнение Клаузиуса26)
- •1.12. Уравнение Менделеева27 - Клапейрона28
- •1.13. Барометрическая формула. Распределение Больцмана
- •1.14. Средняя длина свободного пробега молекул
- •II. Термодинамика
- •2 .1. Термодинамический метод
- •2.2. Внутренняя энергия
- •Два способа изменения внутренней энергии. Теплота и работа
- •Первое начало термодинамики
- •Нулевое начало термодинамики
- •Теплоёмкость
- •1). Молярная теплоёмкость идеального газа при постоянном объёме
- •2). Молярная теплоёмкость идеального газа при постоянном давлении Уравнение Майера
- •Термический кпд для кругового процесса
- •Из истории тепловых двигателей
- •Цикл Карно38
- •Второе начало термодинамики
- •Энтропия
- •2.16. Статистическая интерпретация второго начала термодинамики
- •Реальные газы
- •Жидкости
- •Твёрдые тела
- •Изоморфизм и полиморфизм кристаллов
- •Кристаллические вещества Типы кристаллических решеток
- •Общая характеристика
- •Классификация решёток по симметрии
- •Объём ячейки
Потенциальная энергия тела, поднятого над поверхностью Земли
Сила тяжести равна = m и направлена по вертикали вниз. Вблизи поверхности Земли ее можно считать постоянной. При движении тела по вертикали вниз сила тяжести совпадает по направлению с перемещением. При переходе с высоты h1 над каким-то уровнем, от которого мы начинаем отсчет высоты, до высоты h2 над тем же уровнем (рис. 53), тело совершает перемещение, по абсолютной величине равное h1 – h2.
Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна: A = mg(h1 – h2).
Высоты h1 и h2 не обязательно отсчитывать от поверхности Земли. Для начала отсчета высот можно выбрать любой уровень. Это может быть пол комнаты, стол или стул, это может быть и дно ямы, вырытой в земле, и т. д. Ведь в формулу для работы входит разность высот, а она не зависит от того, откуда начинать их отсчет. Мы могли бы, например, условиться начинать отсчет высоты с уровня В (рис. 51).

Рис. 51.
Тогда высота этого уровня была бы равна нулю, а работа выражалась бы равенством: A = mgh, где h — высота точки A над уровнем В.
Если тело движется вертикально вверх, то сила тяжести направлена против движения тела и ее работа отрицательна.
Если после подъема вверх тело возвращается в исходную течку, то работа на таком пути, начинающемся и кончающемся в одной и той же точке (на замкнутом пути), на пути «туда и обратно», равна нулю. Это одна из особенностей силы тяжести: работа силы тяжести на замкнутом пути равна нулю.
Теперь выясним, какую работу совершает сила тяжести в случае, когда тело движется не по вертикали. В качестве примера рассмотрим движение тела по наклонной плоскости (рис. 52).

Рис. 52.
Допустим,
что тело массой m
по наклонной плоскости высотой h
совершает
перемещение S,
по абсолютной величине равное длине
наклонной плоскости. Работу силы тяжести
mg
в
этом случае надо вычислять по формуле:
A
= mg .
.
Но
из рисунка видно, что
=
 . Поэтому: A
= mgS
.
. Поэтому: A
= mgS
.
Мы получили для работы то же самое значение. Выходит, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. При одной и той же «потере высоты» работа силы тяжести одинакова (рис. 53).

Рис. 53.
Это справедливо не только при движении по наклонной плоскости, но и по любому другому пути. В самом деле, допустим, что тело движется по какому-то произвольному пути, например по такому, какой изображен на рисунке 54.

Рис. 54.
Весь этот путь мы можем мысленно разбить на ряд малых участков: AA1, A2A1, A2A3 и т. д. Каждый из них может считаться маленькой наклонной плоскостью, а все движение тела на пути АВ можно представить как движение по множеству наклонных плоскостей, переходящих одна в другую. Работа силы тяжести на каждой такой наклонной плоскости равна произведению mg на изменение высоты тела на ней. Если изменения высот на отдельных участках равны h1, h2, h3 и т. д., то работы силы тяжести на них равны mgh1, mgh2, mgh3 и т. д. Тогда полную работу на всем пути можно найти, сложив все эти работы: A = mgh1 +mgh2 + … = mg(h1 + h2 + …).
Ho, h1 + h2 + … = h. Следовательно, A = mgh.
Таким образом, работа силы тяжести не зависит от траектории движения тела и всегда равна произведению силы тяжести на разность высот в исходном и конечном положениях. При движении вниз работа положительна, при движении вверх — отрицательна. Эта работа численно равна потенциальной энергии тела над поверхностью земли: П = mgh. Почему же в технике и быту при подъеме грузов часто пользуются наклонной плоскостью? Ведь работа перемещения груза по наклонной плоскости такая же, как и при движении по вертикали! Это объясняется тем, что при равномерном движении груза по наклонной плоскости сила, которая должна быть приложена к грузу в направлении перемещения, меньше силы тяжести. Правда, груз при этом проходит больший путь. Больший путь — это плата за то, что по наклонной плоскости груз можно поднимать с помощью меньшей силы. Связь между потенциальной энергией и силой поля
Т.к.
выполняются соотношения:
где dП – убыль потенциальной энергии в направлении перемещения d . Последняя формула устанавливает связь между потенциальной энергией и силой поля. Взаимодействие тел можно описать либо с помощью сил, либо с помощью потенциальной энергии. В классической механике широко используются оба способа. Однако первый способ обладает большей общностью, т.к. он применим и к диссипативным силам, для которых нельзя ввести потенциальную энергию. В квантовой механике, описывающей явления микромира, диссипативных сил нет. В уравнения квантовой механики входит лишь потенциальная энергия взаимодействующих микрочастиц. Величины, количественно описывающие силовое поле Количественными характеристиками силового поля являются напряжённость и потенциал поля. а). Напряжённость поля Силовой характеристикой поля является напряжённость поля. Опыт показывает, что в случае гравитационных и электростатических взаимодействий сила , действующая на частицу, помещённую в некоторую точку соответствующего поля, пропорциональна массе m (в случае гравитационного поля) или электрическому заряду q (в случае электростатического поля) частицы. В этом случае говорят о массе как «гравитационном заряде». Напряжённостью силового поля называется векторная величина, равная отношению силы, действующей со стороны на помещенную в него материальную частицу, к величине массы (в случае гравитационного поля) или электрического заряда (в случае электростатического поля) этой частицы:
Направление
векторов напряжённости ( Пример. Гравитационное поле (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел, например Солнца и планет Солнечной системы, планет и их спутников, Земли и находящихся на ней или вблизи нее тел. Представим закон всемирного тяготения для двух материальных частиц (рис. 55):
Рис. 55.
1
=
2
=
где 1 и 2 – силы притяжения соответствующих частиц 1 и 2; m1 и m2 – массы частиц; -–гравитационная постоянная.
Если
обозначить массу частицы, создающей
поле М, массу «пробной» частицы,
вносимой в поле m
(m Из последней формулы следует, что напряжённость гравитационного поля, создаваемого частицей массой M, равна:
=
=
Единица
измерения в СИ:
[ б). Потенциал поля Для потенциальных силовых полей можно ввести их энергетическую характеристику – потенциал. В широком понимании потенциал12 - это характеристика векторных полей, к которым относятся многие силовые поля, в т.ч. гравитационное и электромагнитное. В более узком смысле: Потенциал – это скалярная энергетическая характеристика потенциального силового поля, равная отношению потенциальной энергии взаимодействия частицы с полем к массе m этой частицы (в случае гравитационного поля), либо к величине заряда ϥ частицы ( в случае электростатического поля):
Пример. Докажем, что гравитационное поле потенциально. Пусть частица массой m движется в гравитационном поле частицы массой М из точки 1 в точку 2 поля по произвольной траектории. Работа сил поля:
А12
=
=
Mm(
Тогда
потенциал гравитационного поля:
= | Принцип суперпозиции полей При наличии нескольких (n) потенциальных полей их напряжённости в каждой точке пространства складываются геометрически, а их потенциалы – алгебраически:
=
Связь вектора напряжённости силового поля и разности потенциалов. Понятие о градиенте скалярной функции координат
Т.к.
элементарная работа
=
(
В
векторном анализе вектор с компонентами
{ Используя эти обозначения, можно записать: = grad или
=
Напряжённость силового поля равна градиенту потенциала данной точки поля со знаком минус. Знак «минус» в вышеприведённых формулах означает, что вектор напряжённости силового поля направлен в сторону убывания потенциала
Связь
между
и
d
=
где
– угол
между векторами
и
d
; dS
=
| d Понятие о «потенциальной яме» «Потенциальной ямой» называется область пространства, в которой потенциальная энергия U частицы меньше некоторого значения Umax. Термин «потенциальная яма» происходит от вида графика, изображающего зависимость потенциальной энергии U частицы в силовом поле от её положения в пространстве (в случае одномерного движения от координаты x; рис.56). Такая зависимость U(x) возникает в поле сил притяжения.
Рис.56. Схематическое изображение одномерной потенциальной ямы U(x). Полная энергия частицы – сохраняющаяся величина, поэтому изображена на графике горизонтальной линией.
В
частности, при U
= U(x)
и Umax
=
Примером потенциальной ямы может служить потенциал притяжения между протоном и нейтроном, экспоненциально убывающий с увеличением расстояния между ними. В классической механике частица с энергией < 0 не сможет вылететь из потенциальной ямы и будет всё время двигаться в ограниченной области пространства внутри ямы (между двумя классическими точками остановки U0 = ). Положение частицы на «дне» ямы отвечает устойчивому равновесию и соответствует нулевой кинетической энергии частицы. Если > U0, то частица преодолевает действие сил притяжения и свободно покидает яму. Пример – движение упругого шарика, находящегося в поле сил земного притяжения, в обычной яме с жёсткими пологими стенками. В квантовой механике, в отличие от классической, энергия частицы, находящейся в связанном состоянии в потенциальной яме может принимать лишь определённые дискретные значения, т. е. существуют дискретные уровни энергии. Однако такая дискретность уровней становится заметной лишь для систем, имеющих микроскопические размеры и массы. Если в потенциальную яму попала частица, энергия которой ниже, чем необходимая для преодоления краёв ямы, то возникнут колебания частицы в яме. Амплитуда колебаний будет обусловлена собственной энергией частицы. Частица, находящаяся на дне потенциальной ямы, пребывает в состоянии устойчивого равновесия, то есть при отклонении частицы от точки минимума потенциальной энергии возникает сила, направленная в противоположную отклонению сторону. Если частица подчиняется квантовым законам, то, несмотря на недостаток энергии, она с определённой вероятностью может покинуть потенциальную яму (явление туннельного эффекта). Потенциальная яма, удовлетворяющая условию: U(x)
=
при x
< 0; x
> L
и U(x)
= 0 при 0
|
называется одномерной потенциальной ямой бесконечной глубины с плоским дном или «потенциальным ящиком» (рис. 57).

Рис. 57.
|
|
Понятие о «потенциальном барьере»
Потенциальный барьер — противоположное понятие. Это область пространства, где присутствует локальный максимум потенциальной энергии.
Потенциальный барьер – ограниченная в пространстве область высокой потенциальной энергии частицы в силовом поле, по обе стороны которой потенциальная энергия более или менее резко спадает.
Потенциальный барьер соответствует силам отталкивания.
На рис. 58 изображен потенциальный барьер простой формы для случая одномерного (по оси х) движения частицы. В некоторой точке х = x0 потенциальная энергия V(х) принимает максимальное значение V0,называется высотой потенциального барьера. Потенциальный барьер делит пространство на две области (I и II), в которых потенциальная энергия частицы меньше, чем внутри потенциального барьера (в области III).

Рис. 58.
В классической механике прохождение частицы через потенциальный барьер возможно лишь в том случае, если её полная (кинетическая + потенциальная) энергия превышает высоту потенциального барьера. ≥ V0; тогда частица пролетает над барьером. Если же энергия частицы недостаточна для преодоления барьера, < V0, то в некоторой точке x1 частица, движущаяся слева направо, останавливается и затем движется в обратном направлении. То есть потенциальный барьер является как бы непрозрачной стенкой, барьером, для частиц с энергией, меньшей высоты потенциального барьера — отсюда название «потенциальный барьер». В квантовой механике, в отличие от классической, возможно прохождение через потенциальный барьер частиц с энергией < V0 (это явление называется «туннельным эффектом») и отражение от потенциального барьера частиц с > V0. Такие особенности поведения частиц в квантовой физике непосредственно связаны с корпускулярно-волновой природой микрочастиц.
На рис. 59 изображён простейший одномерный потенциальный барьер прямоугольной формы.

Рис. 59.
Поле центральных сил
Центральной силой называется приложенная к телу сила, линия действия которой при любом положении тела проходит через некоторую определённую точку, называемую центром силы.
Примером центральных сил являются сила тяготения, направленная к центру планеты, кулоновские силы электростатического притяжения и отталкивания и др. (рис. 60).
Центральная сила зависит только от расстояния r между взаимодействующими частицами: = ( ).

Рис. 60. Движение двух тел вокруг центра масс O.
Рассмотрим работу при перемещении материальной точки в поле центральных сил (рис. 61): точка 0 – силовой центр.
М

0
Рис. 61.
Элементарная работа по перемещению точки М в поле центральных сил:
= ( ) d
Работа перемещения точки М на конечном участке траектории 1 – 2:
A12
=
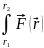 d
=
Ф(
2)
- Ф(
1),
(1)
d
=
Ф(
2)
- Ф(
1),
(1)
где Ф( ) первообразная функции ( ).
Значение определённого интеграла в формуле (1) зависит только от расстояний r1 и r2 точек 1 и 2 до силового центра 0, но не зависит от формы пути, по которому материальная точка М перешла из положения 1 в положение 2.
Таким образом, поле центральных сил – поле потенциальное, а центральные силы – консервативные.
Работа консервативных сил равна убыли потенциальной энергии: = - dП, т.е.
dП = - = - ( ) d . (2)
Проинтегрировав
(2), получим: П
= -
 ,
,
т.е. потенциальная энергия частицы, находящейся в поле центральных сил, зависит только от расстояния до силового центра: П = П( ).
Особый
интерес представляют силы, обратно
пропорциональные квадрату расстояния
до силового центра (гравитационные,
электростатические силы). Для них функция
 имеет вид:
=
имеет вид:
=
 ,
где
- постоянная величина (
> 0 при отталкивании от центра;
< 0 – в случае притяжения к центру).
,
где
- постоянная величина (
> 0 при отталкивании от центра;
< 0 – в случае притяжения к центру).
Проинтегрировав
последнюю формулу, получим: П
= -
 =
=

 .
.
Потенциальную
энергию на бесконечности (r
 )
считают равной нулю, следовательно: П
=
.
Так в случае гравитационного поля:
= -
mM,
получаем:
)
считают равной нулю, следовательно: П
=
.
Так в случае гравитационного поля:
= -
mM,
получаем:
П
= -
 - потенциальная энергия частицы массой
m в гравитационном
поле планеты массой M.
- потенциальная энергия частицы массой
m в гравитационном
поле планеты массой M.

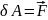 •d
=
•d
=
 или
•d
=
•dS
=
или
•d
=
•dS
=

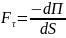 ,
, =
– в
случае гравитационного поля;
=
– в
случае гравитационного поля; =
=
 – в
случае электростатического поля.
– в
случае электростатического поля. )
совпадает
по направлению с вектором силы
.
Величинs
массы m
и
заряда q
должны быть так малы (m
;
q
)
совпадает
по направлению с вектором силы
.
Величинs
массы m
и
заряда q
должны быть так малы (m
;
q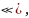 чтобы
поле не искажалось.
чтобы
поле не искажалось.


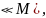 а
расстояние между частицами r,
то силу притяжения можно записать в
виде:
=
а
расстояние между частицами r,
то силу притяжения можно записать в
виде:
=
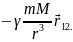

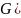 =
.
Т.е. размерность совпадает с
размерностью ускорения. Напряжённость
поля тяготения вблизи поверхности
Земли равна ускорению свободного
падения
(c точностью до поправки,
обусловленной вращением Земли).
=
.
Т.е. размерность совпадает с
размерностью ускорения. Напряжённость
поля тяготения вблизи поверхности
Земли равна ускорению свободного
падения
(c точностью до поправки,
обусловленной вращением Земли). ,
(
,
(
 )
– для
гравитационного поля;
)
– для
гравитационного поля; ,
(В)
– для
электростатического поля.
,
(В)
– для
электростатического поля. где
=
где
=

 Тогда
А12
=
Тогда
А12
=
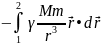 =
=

 ),
т.е. работа сил гравитационного
поля не зависит от формы траектории
материальной частицы, а определяется
положением её начальной и конечной
точек перемещения.
),
т.е. работа сил гравитационного
поля не зависит от формы траектории
материальной частицы, а определяется
положением её начальной и конечной
точек перемещения. .
.



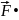 d
=
d
=
 а
а
 =
=
 d
,
то получаем:
d
=
d
,
то получаем:
d
=
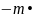 d
или
• d
= d
d
или
• d
= d Учтём, что
=
-–напряжённость гравитационного
поля. Тогда последнее соотношение
примет вид:
•
d
=
Учтём, что
=
-–напряжённость гравитационного
поля. Тогда последнее соотношение
примет вид:
•
d
=
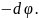
 +
+
 +
+
 ).
). называется
градиентом функции
и
обозначается либо grad
(градиент
),
либо символом
называется
градиентом функции
и
обозначается либо grad
(градиент
),
либо символом
 («набла»),
называемом так же оператором Гамильтона13
(гамильтонианом).
(«набла»),
называемом так же оператором Гамильтона13
(гамильтонианом).
 можно
также представить в виде:
можно
также представить в виде:
 •cos
=
•cos
=
 dS
dS – проекция
вектора
на
направление вектора d
– проекция
вектора
на
направление вектора d

 имеется потенциальная яма бесконечной
глубины.
имеется потенциальная яма бесконечной
глубины. x
L
x
L