
- •Оглавление
- •Часть I. Механика 4
- •Часть II. Молекулярная физика и термодинамика 81
- •Часть I. Механика
- •Кинематика
- •Основные понятия кинематики
- •З.2. Скорость
- •Среднее ускорение
- •Мгновенное ускорение
- •Ускорение точки при прямолинейном движении
- •Кинематика вращательного движения
- •4. Динамика
- •Закон всемирного тяготения
- •2). Сила тяжести
- •3). Сила реакции опоры
- •4). Сила трения
- •Виды трения
- •5). Сила упругости
- •4.4. Импульс. Закон сохранения импульса
- •История появления термина
- •4.5. Законы Ньютона
- •Замечания:
- •4.6. Энергия
- •Потенциальная энергия тела, поднятого над поверхностью Земли
- •Закон сохранения энергии в механике
- •4.7. Динамика вращательного движения
- •2). Пара сил
- •Момент импульса
- •Механический (классический) принцип относительности (принцип относительности Галилея)
- •Основы механики жидкостей и газов
- •Архимед из СиракузArchimedes of Siracuse, ок. 287–212 г. До н. Э.
- •Условие плавания тел
- •Вязкость газов
- •Часть II. Молекулярная физика и термодинамика
- •I. Молекулярная физика
- •1.1. Предмет молекулярной физики
- •1.2. Внесистемные единицы измерения величин в микрофизике физике
- •1.3. Основные положения молекулярно-кинетической теории строения вещества
- •1.4. Число степеней свободы молекул
- •1.5. Термодинамическая система. Термодинамические состояние и процесс
- •1.6. Статистический метод в молекулярной физике
- •1.7. Количество вещества. Масса молекул
- •1.8. Идеальный газ
- •1.9. Закон равномерного распределения энергии по степеням свободы молекул
- •1.10. Закон Максвелла25 о распределении молекул идеального газа по скоростям
- •Вывод распределения по Максвеллу
- •Границы применимости
- •Зависимость функции распределения Максвелла от температуры.
- •Характерные скорости Наиболее вероятная скорость
- •Средняя скорость
- •1.11. Основное уравнение молекулярно – кинетической теории (уравнение Клаузиуса26)
- •1.12. Уравнение Менделеева27 - Клапейрона28
- •1.13. Барометрическая формула. Распределение Больцмана
- •1.14. Средняя длина свободного пробега молекул
- •II. Термодинамика
- •2 .1. Термодинамический метод
- •2.2. Внутренняя энергия
- •Два способа изменения внутренней энергии. Теплота и работа
- •Первое начало термодинамики
- •Нулевое начало термодинамики
- •Теплоёмкость
- •1). Молярная теплоёмкость идеального газа при постоянном объёме
- •2). Молярная теплоёмкость идеального газа при постоянном давлении Уравнение Майера
- •Термический кпд для кругового процесса
- •Из истории тепловых двигателей
- •Цикл Карно38
- •Второе начало термодинамики
- •Энтропия
- •2.16. Статистическая интерпретация второго начала термодинамики
- •Реальные газы
- •Жидкости
- •Твёрдые тела
- •Изоморфизм и полиморфизм кристаллов
- •Кристаллические вещества Типы кристаллических решеток
- •Общая характеристика
- •Классификация решёток по симметрии
- •Объём ячейки
Замечания:
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде: m =

или, = .
Второй закон Ньютона, как и вся классическая механика, действителен только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света ( , используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.
Следует учитывать, что нельзя рассматривать частный случай (при
 )
второго закона как эквивалент первого,
так как первый закон постулирует
существование ИСО, а второй формулируется
уже в ИСО.
)
второго закона как эквивалент первого,
так как первый закон постулирует
существование ИСО, а второй формулируется
уже в ИСО.
Третий закон Ньютона
Механическое воздействие тел друг на друга носит характер взаимодействия. Об этом утверждает третий закон Ньютона:
Две материальные точки действуют друг на друга с силами, которые численно равны и направлены в противоположные стороны вдоль прямой, соединяющей эти точки (рис. 42): 1 = 2.

Рис. 42.
Одна из этих сил называется действующей, а другая -–противодействующей. Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.
Пример.
1). В электростатике взаимодействие электрических зарядов подчиняется третьему закону Ньютона (рис. 43):

Рис. 43.
2). Для силы Лоренца третий закон Ньютона не выполняется.
4.6. Энергия
При движении механической системы меняются координаты и скорости входящих в неё тел. Однако существуют характеризующие систему величины, которые с течением времени остаются постоянными. Такими величинами являются в механике энергия, импульс и момент импульса.
Эне́ргия (Е, W) — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
В СИ: [E, W] = Дж.
Термин «энергия» происходит от слова energeia, которое впервые появилось в работах Аристотеля (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь»). В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия живая сила.
Энергия системы является функцией состояния, а не процесса: она не зависит от того, каким образом достигнуто данное состояние.
С фундаментальной точки зрения энергия представляет собой интеграл движения (то есть сохраняющуюся при движении величину), связанный, согласно теореме Нётер, с однородностью времени. Таким образом, введение понятия энергии как физической величины целесообразно только в том случае, если рассматриваемая физическая система однородна во времени.
В соответствии с различными формами движения материи выделяют различные виды энергии: механическую, внутреннюю, электромагнитную, химическую, ядерную и др.
Механика различает потенциальную энергию (или, в более общем случае, энергию взаимодействия тел или их частей между собой или с внешними полями) и кинетическую энергию (энергия движения). Их сумма называется полной механической энергией.
Энергией обладают все виды полей. По этому признаку различают: электромагнитную (разделяемую иногда на электрическую и магнитную энергии), гравитационную и ядерную энергии (также может быть подразделяться на энергию слабого и сильного взаимодействий).
Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы.
В химии рассматриваются такие величины, как энергия связи и энтальпия, имеющие размерность энергии, отнесённой к количеству вещества.
В механике рассматривается только механическая энергия.
Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна
E = mc2 ,
где E — энергия системы, m — её масса, c — скорость света в вакууме.
Работа силы
Для количественного описания процесса обмена энергией между взаимодействующими телами в механике используется понятие работы силы, приложенной к рассматриваемому телу. Работа силы – это энергетическая характеристика движения.
Понятие работы в физике отличается от её обыденного, физиологического понимания как всякого усилия, мускульного напряжения.
Пусть материальная частица М под действием переменной силы перемещается по криволинейной траектории из точки S1 в точку S2 (рис. 44). Выделим элементарный участок пути dS, на котором силу можно считать постоянной, а перемещение прямолинейным.
 Рис.
44.
Рис.
44.
Уравнение
второго закона Ньютона для частицы М
в этом случае имеет вид: d
=
•dt.
Умножив скалярно обе части этого
равенства на скорость частицы
,
получим:
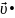 d
=
•
•dt,
где
• dt
= d
d
=
•
•dt,
где
• dt
= d .
В данном случае d
– вектор перемещения. Тогда можно
записать:
.
В данном случае d
– вектор перемещения. Тогда можно
записать:
 А
=
•
d
=
•d
,
где
А11
– элементарная работа силы не перемещении
d
.
А
=
•
d
=
•d
,
где
А11
– элементарная работа силы не перемещении
d
.
Элементарной
работой
А
силы
на перемещении d
называется
скалярное произведение
А=
•
d
= F•
cos
•dS
=

Работа
на пути конечной длины (S1S2)
выражается через криволинейный интеграл:
А =
 =
=
Механическая работа — это скалярная физическая величина, являющаяся количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы.
Если рассматриваемая сила постоянна ( = соnst), а тело, к которому она приложена, движется поступательно и прямолинейно, то работой, совершаемой силой при прохождении телом пути S, называют величину
А
=
|
|
где а -– угол между силой и направлением движения тела (рис. 45).

Рис. 45.
Т.е.
работа (этой силы) равна произведению
величины проекции вектора силы
 на направление движения и величины
совершённого перемещения S.
на направление движения и величины
совершённого перемещения S.
Работа величина алгебраическая:
А > 0 при > 0 – движущая сила; A < 0 при < 0 – тормозящая сила.
Если на тело одновременно действуют несколько сил, то работа, совершаемая ими, равна сумме работ каждой из сил порознь: А = ∑Аi .
Работа не совершается в следующих случаях:
= 0, т.е. на тело сила не действует (например, движение по инерции);
 =
0, т.е. тело покоится;
=
0, т.е. тело покоится;=
 ,
т.е. вектор
силы перпендикулярен к направлению
вектора перемещения (
,
т.е. вектор
силы перпендикулярен к направлению
вектора перемещения ( ).
).
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x) (рис. 46).

Рис. 46.
|
Мощность
Мощность – скалярная физическая величина, численно равная работе, совершаемой за единицу времени:
N
=
 =
=
 =
=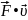 , (Вт).
, (Вт).
Кинетическая энергия
Кинетическая энергия – энергия движущегося тела.
Обозначается: Ек,; Wк; Т; К (Дж).
Пусть
частица массой m
движется под действием силы
 Уравнение второго закона Ньютона для
частицы М в этом случае имеет вид:
d
=
•dt
. Умножив скалярно обе части этого
равенства на скорость частицы
,
получим:
d
=
•
dt
= m
•d
Учтем, что
•d
Уравнение второго закона Ньютона для
частицы М в этом случае имеет вид:
d
=
•dt
. Умножив скалярно обе части этого
равенства на скорость частицы
,
получим:
d
=
•
dt
= m
•d
Учтем, что
•d •d
.
Тогда: m
•d
= m
•d
или m
•d
= d(
•d
.
Тогда: m
•d
= m
•d
или m
•d
= d( ),
где К=
- кинетическая
энергия тела.
),
где К=
- кинетическая
энергия тела.
Тогда кинетическая энергия тела выражается по формуле:
К
=
=
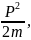
где Р - импульс тела.
Кинетическая
энергия – величина относительная,
всегда выполняется условие: К 0.
0.
Т.к.
d(
)
= dK,
а
d
=
•
•dt
=
 =
=
 Тогда
dK
=
Тогда
dK
=
 при конечном перемещении из точки 1 в
точку 2: ∆К
= А12.
при конечном перемещении из точки 1 в
точку 2: ∆К
= А12.
Тогда в общем случае можно утверждать:
изменение кинетической энергии механической системы равно алгебраической сумме работ всех внешних и внутренних сил, действующих на эту систему: dK = Авнешн. + Авнутр.
Силовое поле
Материя существует в виде вещества и поля. Поле – переносчик взаимодействий между телами (гравитационное, электромагнитное поле, поле ядерных сил и т.п.).
В механике силовое поле – часть пространства, в каждой точке которой на помещенную туда материальную частицу действует сила, зависящая от координат частицы.
Силовое поле называется стационарным, если оно не изменяется со временем.
Потенциальное силовое поле
Стационарное силовое поле, в котором работа сил поля, действующих на материальную частицу, зависит только от начального и конечного положения частицы и не зависит от вида её траектории, называется потенциальным. Силы такого поля называются консервативными.
Если это условие не выполняется, то силовое поле не будет потенциальным ( в частности, вихревым, как магнитное поле).
Потенциальными полями являются: гравитационное, электростатическое, поля центральных сил.
Терема: в потенциальном поле работа сил поля на любом замкнутом пути L равна нулю (рис. 47).

L
Рис. 47.
Доказательство
Т.к. поле потенциальное, то А1а2 = А1b2, но
А1b2= - А2b1. Тогда: А1а2 + А2b1= А1а2 A1b2= 0.
Обратная теорема: если работа сил поля на любом замкнутом пути L равна нулю, то поле потенциальное.
Доказательство
По условию: А1а2 + А2b1 = 0, тогда: А1а2 = - А2b1, но
А2b1 = - А1b2, то А1а2 = А1b2.
Работа сил потенциального поля на произвольном замкнутом пути L выражается через криволинейный интеграл:
А11
=

 0,
0,
где

 0 – циркуляция
вектора
вдоль замкнутой кривой L.
0 – циркуляция
вектора
вдоль замкнутой кривой L.
Условие: 0 является необходимым и достаточным условием потенциальности поля.
Потенциальная энергия
Для частицы, находящейся в потенциальном поле, можно ввести понятие потенциальной энергии.
Потенциальная энергия – часть механической энергии системы, зависящая от взаимного расположения материальных точек, составляющих эту систему, и от их положения во внешнем силовом поле.
Обозначается: Еп,; Wп; U; V;П (Дж).
Т.е. потенциальная энергия есть функция координат частицы в поле: П = П (x, y, z) или П = П( ).
Пусть
материальная частица перемещается в
потенциальном поле сил из разных i
–ых точек в фиксированную точку 0
(рис. 48). Т.к. поле потенциальное, то работа
сил поля при фиксированной точке 0
зависит только от положения i
– той точки. Найдём работу сил
поля при перемещении частицы из точки
1 в точку 2. Т.к. работа не зависит от пути,
выберем путь, проходящий через точку
0. Тогда работа на пути 100′ может
быть представлена в виде: A10′
= A10
+ A00′
= A10
 A00′
. Или с учётом того, что П
= П(
),
получаем: A10′
= П1
П2,
где П1
П2
= - ∆П
– убыль потенциальной энергии.
A00′
. Или с учётом того, что П
= П(
),
получаем: A10′
= П1
П2,
где П1
П2
= - ∆П
– убыль потенциальной энергии.
В
случае элементарной работы:
 =
dП,
т.е. работа
сил потенциального поля (консервативных
сил) равна
убыли потенциальной энергии частицы в
данном поле.
=
dП,
т.е. работа
сил потенциального поля (консервативных
сил) равна
убыли потенциальной энергии частицы в
данном поле.

Рис. 48.
Частице, находящейся в точке 0 поля, можно приписать любое наперёд выбранное значение потенциальной энергии. Математически это выражается в том, что потенциальная энергия П – это функция, которая определяется с точностью до некоторой произвольной постоянной. Однако это обстоятельство несущественно, т.к. во все формулы входит только разность значений потенциальных энергий в двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает. Это соответствует тому обстоятельству, что путём измерения работы может быть определена лишь разность потенциальных энергий в двух точках поля, но не её абсолютное значение.
Т.о. потенциальная энергия – величина относительная, т.е. потенциальная энергия может быть как положительной, так и отрицательной или равной нулю величиной.
В отличие от кинетической энергии, где имеется каноническая формула для расчёта, в случае потенциальной энергии, т.к. она зависит от конфигурации системы и её положения во внешнем силовом поле, такой единой формулы нет.
Пример.
Потенциальная энергия упругой деформации
Примером
силы, модуль которой зависит от координаты,
может служить сила упругости пружины,
подчиняющаяся закону
Гука. Для того, чтобы
растянуть пружину, к ней нужно
приложить внешнюю силу
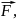 модуль
которой пропорционален удлинению
пружины x
(рис. 49).
модуль
которой пропорционален удлинению
пружины x
(рис. 49).
|
Рис.49.
Растянутая
пружина. Направление внешней силы
совпадает с направлением перемещения
|
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис.50).
|
Рис. 50. Зависимость модуля внешней силы от координаты при растяжении пружины. |
По
площади треугольника на рис. 50 можно
определить работу, совершенную внешней
силой, приложенной к правому свободному
концу пружины: А
=
 ,
где x
– абсолютное
удлинение пружины.
,
где x
– абсолютное
удлинение пружины.
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы упр равна по модулю работе внешней силы и противоположна ей по знаку.
Эта работа численно равна потенциальной энергии упругой деформации:
П = .

 ,
,

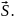 FS
= kx,
где k
– жесткость пружины.
упр.=
FS
= kx,
где k
– жесткость пружины.
упр.=

